37

2. Элементы комбинаторики

Основная задача комбинаторики, как раздела дискретной математики, - пересчет и перечисление элементов в конечных множествах.

Если требуется определить, сколькоэлементов, принадлежащих заданному конечному множеству, обладает некоторым свойством или заданным набором свойств, то это задачапересчета. Если необходимо выделитьвсеэлементы множества, удовлетворяющие заданным свойствам, то это задачаперечисления.

В некоторых задачах на исходном конечном множестве элементов определена некоторая целевая функция, причем нас интересуют элементы множества, соответствующие минимальному или максимальному значению этой функции. В этом случае решается задача оптимизации.

При этом под решением задачи оптимизации в сильном смыслепонимается нахождение всех элементов минимизирующих (максимизирующих) целевую функцию, а под решением задачи оптимизации вслабом смысле- нахождение единственного произвольного элемента.

Рассмотрим основополагающие правила комбинаторики - правила суммы и произведения.

Пусть Х - конечное множество, состоящее из nэлементов х. Тогда говорят, что элемент х из Х может быть выбранnспособами и пишут|Х|=n. Эта запись совпадает с записью мощности множества Х.

Пусть Х₁,...,Х_k- попарно непересекающиеся множества, т.е. Х_iХ_j= ij.

Очевидно, что в этом случае

.

Таково комбинаторное правило суммы. Дляk=2 оно формулируется следующим образом. Если объект х может быть выбранnспособами из множества Х, а объектyиз непересекающегося с ним множестваY, - другимиmспособами, то выбор "х илиy" может быть осуществленn+mспособами.

Правило произведениядляk=2 формулируется следующим образом. Если объект х может быть выбранnспособами и после каждого из таких выборов объектyв свою очередь может быть выбранmспособами, то выбор упорядоченной пары - вектора (х,y) может быть осуществленnmспособами.

Например, Х : {x₁,x₂}, Y : {y₁,y₂}.

Тогда упорядоченные пары (x,y) описываются декартовым произведением

X  Y = {(x₁,y₁),(x₁,y₂),(x₂,y₁),(x₂,y₂)}.

Выбор упорядоченной последовательности из kобъектов вектора (х₁,х₂,...,х_k) может быть осуществленn₁n₂...n_k способами, гдеn_i - число способов выбораi-го объекта х_i,iменяется от 1 доk(записывается:).

В частности, если все n_iравны, что может быть, например, в случае, когда элементы принадлежат одному и тому же множеству, т.е. рассматривается декартово произведение Х^k, то число способов равноn^k.

Наборэлементов х_i1,...,x_ikиз множества Х={x₁,...,x_n}(вектор) называетсявыборкойобъемаkизnэлементов или, иначе, (n,k) выборкой.

Выборка называется упорядоченной, если порядок следования элементов в ней задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.

Если порядок следования элементов не является существенным, то такая выборка называется неупорядоченной.

В выборках могут допускаться и не допускаться повторения элементов, т.е. имеются выборки с повторениемивыборки без повторений.

2.1. Размещения

Упорядоченная (n,k) выборка, в которой элементы могут повторяться, называется (n,k)размещением с повторениями.

Иными словами размещениями с повторениями из nэлементов поkназывают вектора длиныk, составленные изnэлементов множества Х.

Число размещений с повторениями из nэлементов поkопределяется оценкой соответствующего декартова произведения Х^k nэлементного множества, обозначается(по-видимому от английского словаAssign- назначить) и вычисляется следующим образом:

=n^k

Таким образом, первый элемент вектора длины kвыбираетсяnспособами, второй -nспособами и т.д.:

nn...n = n^k.

Пример. Сколькими способами можно оснастить две различные ракеты головными частями трех типов?

Решение. Каждый способ боевого оснащения есть выборка (3,2), вектор длины 2, составленный из 3-х элементного множества типов Т ={t₁,t₂,t₃}. Поэтому число способов боевого оснащения - число размещений с повторениями из 3 по 2:

.

Рассмотрим подробнее:

1) (t₁,t₁); 2) (t₁,t₂); 3) (t₁,t₃);

4) (t₂,t₂); 5) (t₂,t₃); 6) (t₂,t₁);

7) (t₃,t₃); 8) (t₃,t₂); 9) (t₃,t₁).

Получили различные упорядочения двухэлементных векторов из 3-х элементного множества, т.е. множеств Т².

Здесь каждый вектор соответствует способу оснащения. Видно, что, например, (t₁,t₂), (t₂,t₁) считаются разными способами, так как ракеты предполагаются различными ("первая - первым типом", "вторая - вторым" и т.д.). Имеются повторения: (t₁,t₁), (t₂,t₂), (t₃,t₃).

В ряде задач необходимо определить число векторов длины kизnэлементов данного множества без повторения элементов.

Если элементы упорядоченной (n,k) - выборки попарно различны, то они называются (n,k) размещением без повторений или просто (n,k) размещением.

Число таких размещений без повторений обозначается .

Каждое (n,k) размещение без повторения является упорядоченной последовательностью длиныk, члены которой попарно различны и выбираются из множества сnэлементами. Тогда первый член этой последовательности может быть выбранnспособами, после каждого выбора первого члена последовательности второй член может быть выбранn-1 способами и т.д.,k-й член выбираетсяn-(k-1)способом:

=(n-1)(n-2)...[n-(k-1)].

Преобразуем эту формулу, домножая и деля ее на произведение чисел 12(n-k):

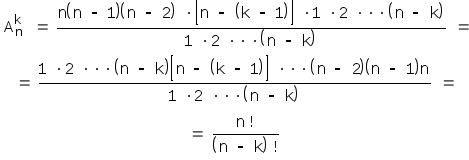
В частности, при k=0. Очевидно, что приk>n=0.

Пример. Сколькими способами из 3-х курсантов можно назначить наряд в составе дежурного и дневального?

Речь идет о выборе упорядоченных двухэлементных подмножеств множества курсантов, состоящего из трех элементов (K={1,2,3}), т.е. о размещениях без повторений из 3 элементов по 2, поэтому

.

Подробнее, в виде векторов из номеров курсантов, например, по журнальному списку, первая компонента которого обозначает номер курсанта - дежурного, вторая - дневального:

(1,2), (1,3), (2,1), (2,3), (3,1), (1,3).

Ясно, что здесь существенен порядок следования компонент и не может быть повторений (один курсант не может быть дежурным и дневальным одновременно), поэтому это множество - подмножество декартового произведения.

Пример.

Сколькими способами можно провести распределение 10 целей по 3 пусковым установкам? Одна пусковая установка назначается для поражения одной цели.

Распределение целей - размещение без повторений из 10 элементов по 3, поэтому

.