а длина всей ломаной M0M1... Мn равна

Функция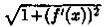 непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:

Вычисление объема тела Вычисление объема тела по известным площадям параллельных сечений

Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.

1.Через произвольную точку х є [a;b] проведем плоскость ∏, перпендикулярную оси Ох (см. рис. 188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x) считаем известной и непрерывно изменяющейся при изменении х. Через v(x)

обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; х] величина v есть функция от х, т. е. v = v(x) (v(a) = 0, v(b) = V).

2.Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.

3.Находим искомую величину V путем интегрирования dV в пределах от а до b:

Полученная формула называется формулой объема тела по площади параллельных сечений. Объем тела вращения

Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х), отрезком а ≤ x ≤ b и прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х [а; b]), есть круг с радиусом у = ƒ(х). Следовательно, S(x)=πy2.

Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком не прерывной функции х=φ(у) ≥ 0 и прямыми х = 0, у = с, у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен

11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.

где (uk)k N — заданная числовая последовательность, называется числовым рядом. Конечные суммы S1 = u1, S2 = u1 + u2, .... Sn = u1 + u2 +...+ un, называются частичными суммами ряда (1).

Если существует конечный предел последовательности частичных сумм (2)

то ряд (1) называется сходящимся, а число S—суммой ряда (1)

Необходимое условие сходимости:

10

Критерий Коши:

Для того чтобы числовой ряд (1) был сходящимся, необходимо и достаточно, чтобы для любого ε > 0 существовало N = N(ε) такое, что для всех n > N и р = 1, 2, … выполнялось неравенство:

Доказательство:

=>

Частный случай:

При p=1: |xn+1| < ε, следовательно, (необходимое условие сходимости ряда).

12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.

Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.

Пусть теперь p>1. Выберем ε так, что p-ε>1. Тогда из левой части неравенства (10) следует, что при n>N выполняется un 1 1 или un+1>un, то есть члены un

ряда возрастают с возрастанием номера n. Поэтому nlim un≠0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.

Замечания:

1.Если расходимость ряда установлена с помощью признака Даламбера, то nlim un≠0.

2.При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.

3.Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.

и пусть существует предел lim n un p. При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

n

Доказательство:

11

Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n>N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).

Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие

p-E >1. Тогда из (14) получаем nun >1 или un>1, следовательно, nlim un≠0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.

13. Интегральный признак Коши сходимости числового ряда.

Пусть члены знакоположительного числового ряда u1+u2+…+un… (7) не возрастают: u1≥u2≥…≥un≥… и пусть f(x) такая положительная, непрерывная, невозрастающая на промежутке [1;∞) функция, что f(1)=u1, f(2)= u2 ,…, f(n)= =un,… . Тогда ряд (7) сходится или расходится одновременно с

Доказательство:

Построим график функции y=f(x) на отрезке [1;n] и построим прямоугольники с основаниями [1;2], [2;3], …, [n-1;n] и высотами u1,u2,…,un-1, а также с высотами u2,u3,…,un.

Sn=u1+u2+…+un-1+un,

Sвпис=u2∙1+u3∙1+…+un∙1 = u2+u3+…+un = Sn-u1, (u1 нет, так как ряд начинается с 1, а не с 0 и отрезка [0;1] нет) Sопис=u1∙1+u2∙1+…+ +un-1∙1 = Sn-un. (так как u1 – это площадь внешнего прямоугольника с основанием [1;2] и высотой u1)

n

Площадь криволинейной трапеции S= f (x)dx . Получаем

1

Sвпис < S < Sопис n

Sn-u1 < f (x)dx < Sn-un.

1

Отсюда:

n

означает, что последовательность частичных сумм Sn ряда (7) ограничена и, следовательно, ряд (7) сходится. Пусть f (x)dx расходится. Это означает, что

1

n

lim f (x)dx =∞ и тогда из (18) следует, что последовательность частичных сумм Sn ряда (7) неограничена и, следовательно, ряд (7) расходится. Теорема

n 1

доказана.

14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.

Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.

12

Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно.

Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно.

Признак Лейбница:

Если для знакочередующегося числового ряда

Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n).

По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n.

С другой стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение в квадратных скобках положительно и S2n>0, поэтому S2n<u1 для любого n. Таким образом, последовательность частичных сумм S2n возрастает и ограничена, следовательно, существует конечный nlim S2n=S. При этом 0<S≤u1.

то есть данный ряд сходится. Теорема доказана.

Замечания:

1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N. Другими словами - отбрасывание конечного числа членов ряда не влияет на сходимость.

2. Условие un>un+1 не является необходимым. Ряд может сходиться, если оно не выполняется. (ЧЕГО? Это условие, иначе он уже не будет рядом Лейбница и признак не будет работать! Откуда взялось это замечание???)

15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.

Определение. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают:

n 1

Где un(x) – функции переменной x, рассматриваемые на некотором промежутке, например на отрезке [a,b].

Если фиксировать произвольное число x0 є[a,b], получим числовой ряд: un (x0 ) , если такие ряды сходятся для каждого x0 є[a,b], то их суммы

n 1

представляют собой функцию S(x), называемую суммой ряда (1).

Определение. Если при x = x0 ряд (1) сходится, то x0 называется точкой сходимости ряда (1).

Определение. Множество всех значений x, при которых функциональный ряд сходится, называется областью сходимости этого ряда. Очевидно, что в области сходимости функционального ряда его сумма является функцией от x. Будем ее обозначать S(x).

— n-ная частичная сумма.

Ряд называется сходящимся равномерно, если последовательность Sn(x) его частичных сумм сходится равномерно. Отличие поточечной сходимости от равномерной:

n>N(ε), для которого |fn(x)-f(x0)|<ε.

,

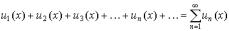составленный из функций, имеющих непрерывные производные 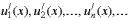, сходится в области C и его сумма равна S(x), а ряд из

13