Ohrimenko+ / Barnsley. Superfractals

Figure 3.69 The orbit of a single set, which looks like a fish, under a group of transformations. Properties that all the fish have in common are geometrical properties of this ‘fish geometry’.

Examples of groups are: the positive rational numbers with × as the binary operation, the unit element being the number 1; the set of invertible n × n matrices for some n N, the unit element being the identity matrix; the set of permutations GA of the alphabet A, in which case the group consists of the set of one-to-one invertible transformations from A into itself and the unit element is I : A → A where I (x) = x for all x X. GA is called the permutation group.

D e f i n i t i o n 3.7.2 A group of transformations on a space X is a group (G(X), ◦), where G(X) consists of one-to-one invertible transformations from X onto X, where the binary operation is composition and where:

(i)the unit element is the identity transformation I : X → X, with I (x) = x for all x X;

(ii)whenever f G we have f −1 G, where f −1 is the inverse of f .

Two important examples of groups of transformations are the group of projective transformations P : R2 L∞ → R2 L∞ and the group of Mobius¨ transformations M : R*2 → R*2, which we discussed in detail in Chapter 2.

We are interested in groups of transformations when they are IFS semigroups. Accordingly, we will use the notation

G{ f1, f2,..., fN }(X)

to denote the IFS semigroup S{ f1, f2,..., fN }(X) only when S{ f1, f2,..., fN }(X) is, in fact, a group of transformations. In this case we will call the IFS semigroup an IFS group.

E x e r c i s e 3.7.4 Show, by means of an example, that an IFS semigroup of invertible transformations is not necessarily an IFS group.

E x e r c i s e 3.7.5 Let G{ f1, f2,..., fN , f1−1, f2−1,..., fN−1}(X) be an IFS group, and let X X have the property that fn (X) fn (X). Show, by means of an example, that it does not follow that the set of functions { f1, f2, . . . , fN , f1−1, f2−1, . . . , fN−1} generates an IFS group on X.

An IFS group is normally called a finitely generated group of transformations. By referring to a finitely generated group of transformation as an IFS group, however, we signal that we are treating it as an IFS semigroup rather than from the point of view of group theory.

We tend to think of IFS semigroups as being associated with IFSs of contractive, or on average contractive, transformations. Similarly we tend to think of an IFS group as being generated by a set of contractive transformations and their inverses. But we do not include these prejudices in the definitions of IFS semigroups and IFS groups because this would be overly restrictive. For example, our broader definition allows us to transpose the theory of orbital sets, measures and pictures, discussed in Sections 3.4–3.6, from IFS semigroups to IFS groups.

In Figure 3.69 we give an example of an orbital set generated by an IFS group of Mobius¨ transformations and in Figures 3.24, 3.68 and 3.79 examples of orbital pictures generated by IFS groups of Mobius¨ transformations. Two examples of

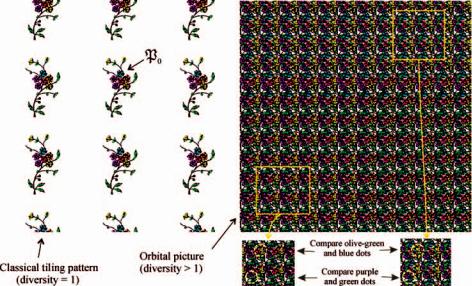
Figure 3.70 Parts of two orbital pictures generated by a crystallographic IFS group. The condensation picture used on the right is a larger version of the one used on the left. The panelling on the right has diversity greater than 4.

orbital pictures generated by IFS groups of projective transformations are shown in Figure 3.75 and examples of orbital pictures generated by IFS groups of euclidean transformations are shown in Figures 3.70 and 3.72–3.74. We discuss some of these examples in the geometry subsections below.

Notice that for IFS groups many different addresses in code space may corre-

spond to the same sequence of transformations. For example, suppose that the IFS group is {X; f1, f2, f3, f4} where f3 = f1−1 and f4 = f2−1. Then

f1132314(P0) = f12314(P0) = f124(P0) = f1(P0),

for all P0 . This has obvious consequences for the computation of orbital sets, measures and pictures associated with IFS groups. To generate addresses without this redundancy, in this case, notice that 1 must be followed by 1, 2 or 4, 2 must be followed by 1, 2 or 3 and so on. Thus the set of all addresses in {1,2,3,4} of length n, which contains 4n distinct strings, can be reduced, by cancellation of adjacent inverse transformations, to a set containing 4 × 3n−1 addresses. To compute an orbital picture associated with this IFS group, we need only consider the reduced set of addresses.

The structure of code spaces associated with IFS groups in the case of four maps, as above, is described very fully, in the context of Mobius¨ transformations, in the book Indra’s Pearls; see [73].

Figure 3.71 Pictures of five different projective IFS objects associated with the same IFS; see Equation (3.5.9). The objects are (i) a set attractor, (ii) an orbital picture, (iii) a colour-rendered fractal top, (iv) a colour-rendered measure attractor and (v) an orbital set. The geometrical property of being a projective IFS object belongs to projective geometry.

The general theory of groups of transformations has been widely studied and there exists a vast body of literature concerning the relationships between geometry, tilings and group theory; see for example [23], [42], [73], [89] and references therein. We shall not describe or review this area, which is essentially classical geometry.

Here we want to connect IFS theory and the associated fractals, orbital sets, orbital measures and pictures, IFS semigroup picture tilings and panellings and so on to classical geometry. We do this, in part, by informally allowing semigroups as well as groups to define geometries.

Figure 3.72 Portions of orbital pictures made using the third crystallographic group. Compare with Figures 3.70 and 3.73. The figure on the right does not represent part of a standard wallpaper pattern. Why?

Figure 3.73 Orbital pictures generated by the fifth cystallographic group. On the left the tiles are nonoverlapping, and a classical wallpaper pattern is the result. But the pattern on the right is not a semigroup tiling because there are different panels, and the pattern varies subtly across the picture. Can you see some of these variations?

E x e r c i s e 3.7.6 Let {X; f1, f2, . . . , fN } denote an IFS of invertible transformations. Prove that S{ f1, f2,..., fN , f1−1, f2−1,..., fN−1}(X) is an IFS group.

Show that S{Rθ }(R2) is a group if and only if θ is a rational number.

where a, b, c, d, e, f R with ad − bc =0. Show that the set of all such transformations forms a group on R2. Show that the set of affine transformations of the form Rθ , see Exercise 3.7.7, with θ rational forms a subgroup of the group of affine transformations on R2.

Geometries and IFS objects

Klein’s elegant idea was that a group of transformations acting on a space defines a geometry.

D e f i n i t i o n 3.7.9 Let G(X) be a group of transformations. Let the transformations of G(X) act upon the space of subsets, S(X), according to

T (S) = {T (x) : x S} for all S S(X),

as in Chapter 1. Then G(X) is called a geometry, and properties of members of S(X) that are invariant under all the transformations of the group are called geometrical properties (of the geometry).

Let us also refer informally, from time to time, to properties that are invariant under the transformations of a semigroup as geometrical properties (of the semigroup).

Given a geometry G = G(X), we extend it to allow the transformations to act on the space of pictures C(X) and the space of normalized Borel measures P(X), when these spaces are well defined. So, for example, when X = R2 we can talk about an invariance property of an orbital picture under the transformations belonging to G as being a geometrical property of G.

Note that the geometry of an IFS group whose transformations are contained in a geometry G may have more properties than G because the smaller the set of transformations, the more invariants they are likely to share. See Exercise 3.7.14 below, for example.

There are many different objects that may be associated with an IFS. They include: orbital sets, measures and pictures; set attractors; measure attractors and fractal tops; panels and tiles. We call them IFS objects. An IFS object is defined by an IFS and possible ancillary information such as a condensation set, measure or picture. Typically it is constructed by repeated applications of the transformations of the IFS. So, when the IFS belongs to a geometry G its IFS objects tend to have properties related to G. In Figure 3.71 we show five different IFS objects, all associated with the same IFS of projective transformations.

When the transformations in an IFS belong to an overarching distinctive group or semigroup G, such as the group of projective transformations, the group of Mobius¨ transformations or the semigroup generated by the inverse branches of a rational function on the Riemann sphere, the corresponding IFS objects tend to have their own distinctive ‘look and feel’, which depends upon the geometrical properties of G. For example, pictures of set attractors of IFSs of similitudes tend to contain angular features, and distinctive patterns of features, that are repeated at all scales of observation. Attractors of Mobius¨ transformations tend to contain angular features that are repeated at all scales of magnification and patterns of features that are seen to recur in a distorted form, owing to the changing ratios between distances. Attractors of projective transformations tend to contain diverse angles and distorted shapes, yet similar incidences and cross-ratios will be repeated over and over again at different scales. If you are shown a picture of an attractor of one of these types, you will rarely mistake it for being of another type; see for example Figure 4.5.

Such a distinctive ‘look and feel’ derives at least in part from the following two factors. (i) The IFS objects have properties that are inherited from G. (ii) The IFS objects themselves provide new properties of G.

Here we elaborate in a general way on these two points. Then, in the following subsections, we discuss properties of specific important geometries and relate them to (i) and (ii).

(i) The IFS objects have properties that are inherited from G. If a condensation set, a condensation measure or a condensation picture possesses a certain geometrical property then the elements of the corresponding orbits under the IFS semigroup will share that property. In turn, these shared properties will be echoed within the corresponding orbital set, measure or picture.

For example, if a panel Qσ of an orbital picture possesses a certain geometrical property then the panels QS◦n (σ ), n = 1, 2, . . . , |σ |, will also have that property. If the IFS consists of Mobius¨ transformations and if the condensation picture possesses a circular boundary then the corresponding panels will possess boundaries that are finite unions of arcs of circles. If a semigroup tiling is generated by an IFS of invertible affine transformations applied to a triangular condensation set then the tiles will be triangular.

Quite generally, it follows from the self-referential equations obeyed by some IFS objects, such as Equations (3.4.1), (3.5.10), (3.5.11) and (3.6.2), as well as those obeyed by set attractors, measure attractors and fractal tops, that an IFS object typically possesses global features (that is, relating to many tiles, segments or panels or to the whole of itself) that are repeated in the object via transformations belonging to the IFS. Since the transformations belong to G, these repeated global features share properties of G. For example Equation (3.5.10) tells us that

Figure 3.74 Orbital pictures generated by the fifth crystallographic group applied to a buttercup picture. Neither is a wallpaper pattern – subtle differences occur in some of the patterns.

any orbital picture P, with a sufficiently rich code space, contains global segments fn (Rn ) that are the images of global segments Rn P. The geometrical properties of Rn are shared by fn (Rn ): an orbital picture generated by a semigroup of euclidean transformations is the union of a finite set of rigid transformations of segments of itself, for instance. You can readily identify parts of global repeated patterns, indicated by distinctive angles and distances, in the orbital pictures illustrated in Figures 3.70 and 3.72–3.74.

(ii) The IFS objects themselves provide new properties of G. Let P denote an orbital picture of an IFS semigroup contained in G. Then if G is the group of affine transformations we may say that P is an affine orbital picture. We will use similar terminology to describe other IFS objects. So for example we may refer to a projective set attractor, a Mobius¨ orbital measure or an affine fractal top.

Let P denote an orbital picture generated by an IFS semigroup contained in a group G. Then g(P) is an orbital picture generated by an IFS semigroup contained in G, for all g G. So, for example, the property of being an affine orbital picture is a geometrical property of affine geometry, Gaffine. This is analogous to saying that the property of being a polygon is a property of affine geometry.

Let P be an orbital picture whose code space is given as P0

Then we say that P is an orbital picture with code space structure P0 .

Now let P denote an affine orbital picture with code space structure P0 . Let g Gaffine. Then it is readily proved that g(P) is an affine orbital picture with the same code space structure. Thus, the property of being an affine orbital picture with a certain code space structure is a property of affine geometry. This is analogous to saying that the property of being a polygon with a certain number of vertices is

a property of affine geometry or that the property of being a triangle with certain angles at the vertices is a property of euclidean geometry.

We can also use invariants associated with dynamical systems, such as the growth rate of periodic orbits, entropy or zeta-functions or related quantities such as the diversity of an orbital picture, to define properties of geometries. For example, let P denote an orbital picture with symbolic entropy 0.8. Then it is readily proved that g(P) is also an orbital picture with symbolic entropy 0.8, for all g G. That is, the property of being an orbital picture with a certain symbolic entropy is a geometrical property of any geometry to which the IFS semigroup belongs.

In Chapter 4 we will extend the notion of code space structure to attractors and fractal tops of contractive IFSs. Then you will see that the following general principle applies: code space structure is a geometrical property. That is, let F be an IFS contained in a group G and let O be an IFS object generated by F; then g(O) has the same code space structure as O for all g G. So for example the property of being a projective set attractor of an IFS, with a certain code space structure, is a property of projective geometry; and the property of being a Mobius¨ fractal top with a certain code space structure is a property of Mobius¨ geometry.

The idea of code space structure as a geometrical invariant becomes particularly exciting when we discover the fractal homeomorphism theorem in Chapter 4: this theorem says that set attractors of IFSs have the same code space structure if and only if they are homeomorphic.

E x e r c i s e 3.7.10 Let P denote an orbital picture generated by an IFS semigroup contained in a group G. Prove that g(P) is an orbital picture generated by an IFS semigroup contained in G, for all g G.

E x e r c i s e 3.7.11 Let P denote an affine orbital picture with code space structure P0 . Let g Gaffine. Prove that g(P) is an affine orbital picture with code space structure P0 .

Euclidean geometry

Euclidean geometry in two dimensions involves two concepts: (i) a plane and (ii) the transformations that rigidly move the plane upon itself. By (i) we mean the euclidean plane, which we represent by R2, as well as subsets of it: lines, circles, triangles, fractals and so on. In this plane we can measure angles between lines and distances between points. By (ii) we mean the euclidean transformations, the set of all mappings that take the plane to itself while preserving angles and distances. euclidean geometry comes into being as the interplay between the plane and the euclidean transformations; this interplay reveals most of what we know about both these entities.

Euclidean geometry is represented by the set of all transformations E : R2 → R2 defined by

E(x, y) = (s(x cos θ − y sin θ ) + e, x sin θ + y cos θ + f ) for all x, y R2

for some set of parameters e, f, θ R; s {−1, +1}.

In addition to preserving distances and angles, the group of euclidean transformations acting on R2 and its subsets has the remarkable property that it admits only seventeen fundamentally different classical euclidean tilings; see [23], vol. 1, Section 1.7, pp. 11–22.

We now explain more carefully what this last statement means. We first note that any given tile, in standard terminology, may correspond to many different sequences of transformations from the group applied to the fundamental tile, namely the condensation picture. But in the theory of IFS semigroups we distinguish between IFS tilings, where each tile has exactly one address in code space, and panellings, where the ‘tiles’ are panels and possess unique addresses

in the space . Thus a tiling under a group of transformations, in standard

P0

nomenclature, corresponds to what we call a panelling of diversity 1.

We say that two panellings are conjugate iff the associated IFSs are conjugate under a transformation T , see Exercise 3.7.3, and the associated orbital pictures are related by P = T (P). We define a classical euclidean tiling to be a panelling of diversity 1, of an orbital picture whose domain is R2, associated with an IFS group of euclidean transformations, for which the domain of the condensation picture is compact and connected.

Then, by our statement above that ‘the group of euclidean transformations acting on R2 admits only seventeen fundamentally different classical euclidean tilings’ we mean more precisely that the picture of any classical euclidean tiling is an orbital picture of an IFS group that is conjugate under an affine transformation to an element of a set of seventeen distinct IFS groups of euclidean transformations. Of course, any element of the set may be replaced by any IFS group that is conjugate to it under an affine transformation. Five of these IFS groups, called the crystallographic groups, may be generated by the following IFSs:

Here each transformation is denoted by the result of applying it to the point (x, y) R2. The remaining twelve IFS groups may be obtained by composing