fiz

усиления тяготения в области залегания руды. На этом явлении основана предварительная разведка полезных ископаемых.

К свободному падению применимы все формулы равноускоренного движения, только в них вместо пути S обычно пишут буквы H или h , обозначающие высоту, а вместо ускорения a – ускорение свободного падения g . Приведем эти формулы:

Здесь y – координата тела на вертикальной оси координат OY , y0 – начальная координата. Там, где

стоит ±, знак «плюс» соответствует случаю, когда тело падает свободно вниз, а знак «минус» – случаю, когда оно брошено свободно вверх и движется с убывающей по модулю скоростью.

Пусть тело брошено свободно вертикально вверх с начальной скоростью 01 . При этом оно будет

двигаться под действием только притяжения планеты равнозамедленно с убывающей по модулю скоростью. Через время t1 оно достигнет высшей точки подъема, где его конечная скорость OX станет

начальной скорости, ведь в высшей точке оно останавливается. Это максимальная высота определяется формулой

gt2 ,

hmax 2

где t – время взлета тела или время его падения.

Когда тело падает в воздухе или иной среде, оказывающей сопротивление его движению, то такое падение нельзя считать свободным и ускорение такого падения меньше ускорения свободного падения. Однако если сопротивление воздуха невелико по сравнению с притяжением тела к планете, то им можно пренебречь и считать падение свободным. Например, можно пренебречь сопротивление воздуха падению камня, а сопротивлением падению листа бумаги пренебречь нельзя, так как из-за малого веса листа, который сравним с сопротивлением воздуха, падение листа не будет свободным и будет происходить с ускорением, меньшим ускорения свободного падения.

С ускорением, большим ускорения свободного падения, тело падает, если на него действует сила, сонаправленная с силой тяготения к планете.

9. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТЕЛ С УСКОРЕНИЕМ СВОБОДНОГО ПАДЕНИЯ

А. Движение тела, брошенного горизонтально

Пусть тело, находящееся на высоте h , брошенного горизонтально со скоростью x . Сопротивлением

воздуха можно пренебречь. При этом на тело будет действовать притяжение планеты, в результате чего оно станет свободно падать в направлении оси OY без начальной скорости. Но поскольку ему в точке O была сообщена горизонтальная скорость x и нет причин, которые заставили бы тело изменить эту

скорость – никакие другие тела на брошенное тело в горизонтальном направлении не действуют, сопротивление среды отсутствует, то тело будет одновременно двигаться и в горизонтальном направлении вдоль оси OX с постоянной по величине и направлению скоростью x . В результате

движение тела будет представлять собой суперпозицию двух движений, происходящих одновременно: равномерного и прямолинейного движения в горизонтальном направлении со скоростью x и свободного

графике изображается плоской кривой линией – параболой (рис. 9-1). Следовательно, тело, брошенное свободно с некоторой высоты в горизонтальном направлении, движется по параболе, ветвь которой направлена вниз, а вершина располагается в точке бросания.

Время падения t с высоты h , равное времени полета на расстояние S , можно найти по формуле

Впроцессе движения тела по параболе его горизонтальная скорость x будет оставаться постоянной,

авертикальная скорость y , которая в точке бросания O была равна нулю ( 0 y 0 ), будет нарастать.

Если сложить векторно скорости x и y , то мы найдем результирующую скорость тела в каждой точке

траектории, по которой оно движется. Вектор этой скорости направлен по касательной к параболе в каждой ее точке и по модулю определяется теоремой Пифагора:

x2 y2 .

Тангенс угла между вектором и горизонтом можно определить отношением:

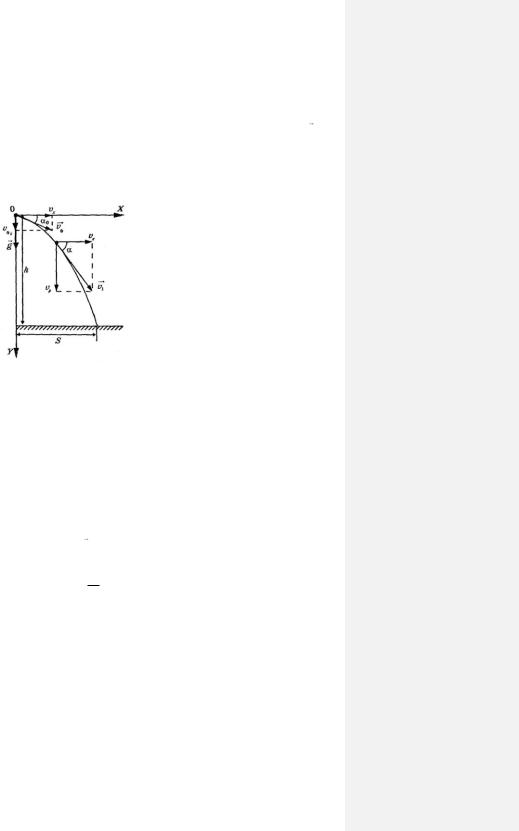
tg x .y

Б. Движение пикирующего тела

Если тело пикирует к земле с высоты h под некоторым углом (рис. 9-3) со скоростью 0 , то теперь у его начальной скорости есть вертикальная составляющая 0 y 0 sin , которая является

начальной скоростью его свободного падения с высоты к вдоль оси OY . Кроме того, у его начальной скорости есть горизонтальная составляющая x 0 cos , с которой оно будет двигаться равномерно

вдоль оси OX (рис. 9-2).

Рис. 9-2

При решении соответствующих задач, кроме приведенных уравнений, вам могут пригодиться формулы

y 0 y gt , 2 x2 y2 , y2 02y 2gh и др.

Угол α между вектором результирующей скорости и горизонтом будет непрерывно увеличиваться. Тангенс этого угла можно определить отношением скоростей y к x :

tg y .x

Траектория движения тела и в этом и случае является параболой, в чем нетрудно убедиться, выразив время из уравнения x 0t cos и подставить его в уравнение

При одинаковой высоте падения дальность полета будет меньше, а скорость падения – больше, чем при горизонтальном бросании с той же скоростью. Вот почему для более точного падения груза на выбранное место при сбрасывании его самолет пикирует. При этом дальность полета груза меньше и прицельность сбрасывания точнее.

В. Движение тела, брошенного под углом к горизонту

Пусть тело брошено под углом к горизонту со скоростью 0 (рис. 9-3). Сопротивлением воздуха можно пренебречь.

Рис. 9-3

При этом опять на тело будет действовать только притяжение планеты вертикально вниз, под действием которого оно будет одновременно участвовать в двух движениях: равномерном и прямолинейном по горизонтали вдоль оси OX и сначала – в равнозамедленном движении вверх убывающей по модулю скоростью до высшей точки подъема, а затем – в свободном падении вниз без начальной скорости вдоль оси OY .

Скорость движения тела вдоль оси OX

Координату тела на оси OX можно определить по формуле x xt 0t cos .

Дальность полета S равна:

S xtî áù 0tî áù cos .

Здесь tî áù – все время полета.

Скорость движения тела вдоль оси OY y будет вначале убывать, пока оно не достигнет высшей

точки подъема, где вертикальная скорость станет рана нулю, а затем при свободном падении с максимальной высоты hmax она будет возрастать. Определить y можно по формуле:

y 0 y gt , где 0 y 0 sin

Угол , под которым тело упадет на землю, равен углу, под которым оно было брошено (эти углы образованы векторами скорости тела и линией горизонта). Скорость тела 0 в момент бросания по

модулю равна скорости в момент падения и время взлета t равно времени падения, а все время полета

Это уравнение параболы, вершина которой находится в высшей точке подъема, а ветви направлены вниз (рис. 9-3). Следовательно, тело, брошенное под углом к горизонту, движется по параболе.

следствие, поднимется на меньшую высоту. Траектория движения тела в этом случае уже не будет представлять собой параболу, а будет выглядеть примерно так, как показано на рис. 9-4. При составлении уравнения кинематики применительно к такому движению необходимо учитывать влияние сопротивления среды на его кинематические параметры.

10. РАВНОМЕРНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ

Равномерным движением материальной точки по окружности называют движение, при котором за любые равные промежутки времени точка проходит дуги одинаковой длины.

Тело, принятое за материальную точку, движется по окружности равномерно, когда суммарное действие на него других тел постоянно по величине и направлено все время по радиусу к центру окружности. Например, камень, раскрученный в вертикальной плоскости на веревке, движется под действием силы натяжения веревки, направленной вдоль нее к руке, держащей веревку за другой конец, спутник движется вокруг Земли под действием притяжения Земли, которое действует на спутник по радиусу его траектории к центру Земли.

Быстроту движения тела по окружности характеризуют линейной скоростью , угловой скоростью, периодом T и частотой вращения v (или n ).

Линейная скорость (или просто скорость) – это скорость, с которой тело движется по окружности. При равномерном движении по окружности вектор линейной скорости остается

Физический смысл линейной скорости: линейная скорость равна длине дуги, пройденной телом за единицу времени при равномерном движении по окружности.

Таким образом, модуль линейной скорости определяется при равномерном движении по окружности так же, как модуль скорости равномерного и прямолинейного движения. Но в отличие от

прямолинейного движения, когда направление вектора скорости остается неизменным в процессе движения, при движении по окружности вектор линейной скорости все время изменяет свое направление, оставаясь перпендикулярным к радиусу этой окружности.

Угловая скорость равномерного движения по окружности равна отношению угла поворота радиуса, соединяющего движущееся тело с центром окружности, ко времени поворота.

Угловая скорость – векторная величина. Вектор угловой скорости сонаправлен с поступательным движением правого винта (буравчика), когда его головка вращается в направлении движения тела по окружности.

На рис. 10-1 вектор угловой скорости направлен за чертеж вдоль оси вращения, проходящей через точку O перпендикулярно плоскости чертежа. Символически такое направление изображается маленьким кружком с крестиком внутри (мы как бы видим оперение стрелы, улетающей от нас за чертеж).

Вектор, направление которого определяется правилом винта (буравчика), называется псевдовектором. Таким образом, вектор угловой скорости это псевдовектор.

Физический смысл угловой скорости: угловая скорость равномерного движения по окружности равна углу поворота радиуса, соединяющего тело с центром окружности, за единицу времени.

Единица измерения угловой скорости в СИ – радиан в секунду (рад/с). Физический смысл этой единицы измерения: 1 рад/с – угловая скорость, при которой за каждую секунду радиус, соединяющий

Равномерное движение по окружности является периодическим, т. е. таким, при котором все положения тела через равные промежутки времени повторяются. Условие периодичности

x t x t NT

Рис. 10-2

Здесь x t – координата тела в момент времени t , N – число полных оборотов тела за время t , x t NT – координата тела через время NT , T – период.

Период T равен отношению времени движения t ко всему числу оборотов N , сделанных за это

Физический смысл периода: период это время, за которое тело совершает один полный оборот. При равномерном движении по окружности период – постоянная величина.

Период – скалярная величина. Единица периода в СИ – секунда.

Условие периодичности (10.3) показывает, что через равное число периодов координата точки, движущейся равномерно по окружности, становится такой же, какой она была через время t от начала отсчета времени движения.

Частота вращения v равна отношению числа оборотов тела N ко времени t , за которое они совершены.

Физический смысл частоты вращения: частота вращения равна числу оборотов тела за единицу времени.

Частота вращения – скалярная величина. Единица частоты вращения в СИ – 1 c-1 .

Физический смысл этой единицы: 1 c-1 – такая частота вращения, при которой за каждую секунду тело совершает один оборот.

Сравнив две последние формулы, получим, что период и частота – обратные величины.

Установим связь между угловой скоростью, периодом и частотой вращения. Если тело совершило

Установим связь линейной скорости с периодом. Поскольку при равномерном движении по окружности

St ,

то, когда t T , путь S равен длине окружности, т. е.

Формула (10.12) устанавливает связь угловой и линейной скоростей: линейная скорость равна произведению угловой скорости и радиуса окружности, по которой движется тело.

Пусть тело движется равномерно по окружности радиусом R . При этом направление вектора линейной скорости непрерывно изменяется. Пусть в точке m линейная скорость тела была 0 , а в точке

n она стала равна , причем модули, т. е. длины векторов 0 и , не изменились (рис. 10-3). Перенесем вектор 0 параллельно самому себе из точки m в точку n и соединим вектором

концы векторов 0 и , направив вектор к концу вектора . Как известно из математики, вектор представляет собой векторную разность векторов 0 и (рис. 10-3).

0

Вектор характеризует изменение линейной скорости по направлению. При малых углах угол между векторами и будет близок к прямому и вектор

будет перпендикулярен вектору . Но вектор , направленный по касательной к окружности, перпендикулярен радиусу окружности R , следовательно, вектор направлен по радиусу к центру окружности.

Если скорость тела изменяется хотя бы по направлению, значит, оно движется с ускорением, которое всегда сонаправлено с вектором изменения скорости , Следовательно, вектор ускорения при таком движении тоже направлен по радиусу к центру окружности, поэтому такое ускорение называется центростремительным ускорением aö (или нормальным ускорением an ).

Центростремительное ускорение характеризует быстроту изменения линейной скорости только

Центростремительное ускорение определяется произведением линейной и угловой скоростей.

Центростремительное ускорение определяется отношением квадрата линейной скорости к радиусу окружности или произведением квадрата угловой скорости и радиуса окружности.

При равномерном движении материальной точки по окружности угловая скорость , частота вращения тела v , период T , модули линейной скорости и центростремительного ускорения aö

остаются постоянными, а увеличиваются с течением времени t угол поворота радиуса и число оборотов N .

11. РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ

Равнопеременным движением материальной точки по окружности называется движение, при котором за любые равные промежутки времени угловая скорость точки изменяется на одинаковую величину.

Очевидно, что при равнопеременном движении по окружности линейная скорость материальной точки тоже изменяется за любые равные промежутки времени на одинаковую величину, ведь линейная и угловая скорости связаны соотношением R , а радиус окружности остается постоянным в течение всего времени движения.

Быстроту поворота радиуса R , соединяющего материальную точку, движущуюся по окружности, с центром окружности, характеризуют средней угловой скоростью cp .

Средняя угловая скорость равна отношению угла поворота радиуса, соединяющего материальную точку с центром окружности, ко времени поворота:

Физический смысл средней угловой скорости: средняя угловая скорость равна углу поворота радиуса, соединяющего материальную точку с центром окружности, за единицу времени.

Единица средней угловой скорости cp в СИ – радиан в секунду (рад/с). Её физический смысл раскрыт в п. 10.

Если в момент времени t 0 начальная угловая скорость точки была равна 0 , а через некоторый

промежуток времени она стала равна , то, поскольку за каждую единицу времени угловая скорость изменялась на одинаковую величину, среднюю угловую скорость можно определить как среднее арифметическое начальной и конечной угловых скоростей:

Угловое ускорение материальной точки, движущейся равнопеременно по окружности, равно отношению изменения угловой скорости ко времени, за которое это изменение произошло:

угловая скорость, t – время изменения угловой скорости.

Физический смысл углового ускорения: угловое ускорение при равнопеременном движении по

Единица углового ускорения в СИ – радиан на секунду в квадрате ( ðàäñ2 ).

Физический смысл рад/с2: 1 рад/с2 – угловое ускорение, при котором за каждую секунду угловая скорость материальной точки изменяется на 1 рад/с.

Поскольку с изменением угловой скорости со изменяется и частота вращения v , то быстрота вращения материальной точки вокруг некоторой оси вращения может быть охарактеризована средней

2 N

Вслучае равнозамедленного движения перед угловым ускорением в формулах (11.10) – (11.12) ставят минус.

12. ПЕРЕМЕННОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ. ПОЛНОЕ УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ МАТЕРИАЛЬНОЙ ТОЧКИ

Пусть материальная точка движется по окружности с переменным угловым ускорением. При этом быстрота поворота радиуса, соединяющего ее с центром окружности, характеризуется средней ñð и

мгновенной угловыми скоростями. Средняя угловая скорость при движении с переменным угловым ускорением определяется так же, как и при равнопеременном движении, отношением угла поворота радиуса ко времени поворота t ,

Однако при переменном угловом ускорении определять среднюю угловую скорость как среднее арифметическое начальной и конечной угловых скоростей, т. е. по формуле (11.2), нельзя, поскольку за любые равные промежутки времени угловая скорость изменяется теперь произвольно.

Мгновенная угловая скорость при переменном движении материальной точки по окружности определяется пределом отношения угла поворота радиуса , соединяющего точку с центром

окружности, к промежутку времени t , за которое этот поворот произошел, при стремлении этого промежутка к нулю,

Угловая скорость равна первой производной угла поворота радиуса, соединяющего материальную точку с центром окружности, по времени.

Угловое ускорение есть предел отношения изменения угловой скорости ко времени t , за которое изменение произошло, при стремлении этого промежутка времени к нулю,