fiz

и подставим полученное выражение в формулу (5.11):

Формула (5.14) устанавливает связь пройденного пути с начальной, конечной скоростями и ускорением тела.

В случае равнозамедленного движения ее можно записать так:

1)скорость тела прямо пропорциональна времени движения;

2)пройденный путь прямо пропорционален квадрату времени движения;

3)за первую секунду тело проходит путь:

S1 a2 12 a2 1 ; Путь S2 , пройденный за вторую секунду, равен:

S2 a2 22 a2 12 a2 3 ;

4) Отсюда следует вывод:

S1 : S2 : S3 :...: Sn 1: 3: 5:...: 2n 1 .

Пути, проходимые телом за последовательные равные промежутки времени, относятся как последовательные нечетные числа.

Рассмотрим графики ускорения, скорости, пути и координаты равнопеременного движения. На рис. 5-3 изображен график ускорения этого движения.

Поскольку при равнопеременном движении ускорение постоянно, то график ускорения, т. е. графическая зависимость ускорения от времени, есть

прямая линия, параллельная оси времени. График ускорения равноускоренного движения располагается над осью времени, а график ускорения равнозамедленного движения – под этой осью.

На рис. 5-4 изображен график скорости равноускоренного движения. Уравнение (5.9) является линейным уравнением, поэтому график

Из рис. 5-4 следует, что ускорение на графике скорости равноускоренного движения численно равно тангенсу угла наклона графика к оси времени,

Следовательно (см. формулу (5.11)), путь на графике скорости равноускоренного движения численно равен площади трапеции, ограниченной графиком и осями координат.

На рис. 5-5 изображены графики равноускоренного движения трех тел 1, 2 и 3, а график 4 соответствует равномерному движению четвертого тела, скорость которого была равна начальной скорости 02 второго тела. Начальные скорости тел 1 и 3 равны нулю, причем первое тело начало

двигаться на время t1 позже третьего. Точка пересечения графиков 1 и 3 означает, что в момент времени t2 скорости тел 1 и 3 стали одинаковы и равны 1 .

Параллельность графиков 2 и 3 означает, что углы наклона этих графиков к оси времени Ot равны1 . А поскольку тангенсы этих углов численно равны ускорению тел, значит тела 2 и 3 движутся с

одинаковыми ускорениями. Из рис. 5-5 следует также, что угол наклона графика 1 (угол 2 ) больше угла наклона графиков 2 и 3. Это значит, что ускорение тела 1 больше ускорений тел 2 и 3.

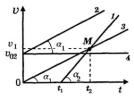Рис. 5-6 Рис. 5-5

График скорости равнозамедленного движения изображен на рис. 5-6. Точка 0 соответствует моменту остановки тела. Путь S , пройденный до остановки графически равен площади заштрихованного прямоугольного треугольника.

нужно провести прямую, касательную к графику в некоторой точке. Тангенс угла наклона этой прямой к оси времени равен скорости тела.

На рис. 5-7 отрезок прямой mn касателен к графику пути в точке M . Тангенс угла наклона этого отрезка к оси времени равен мгновенной скорости тела в момент t1 ,

tg .

Если провести такую касательную к графику-параболе в точке O и эта касательная совпадет с осью времени Ot , т. е. ее угол наклона к оси времени будет равен нулю, то это означает, что скорость тела в

момент начала отсчета времени движения, т. е. начальная скорость, 0 0 . А если такая касательная в

На рис. 5-9 изображены графики координаты равнопеременного движения. График координаты x x t тоже представляет собой параболу, поскольку в формулах (5.12) и (5.13) координата x есть

функция квадрата времени.

Но поскольку координата тела может уменьшаться, например, когда оно возвращается к началу отсчета (движется назад), то на графике координаты парабола может иметь ветви, направленные как вверх, так и в низ. На рис. 5-9 парабола ab соответствует равноускоренному движению в течение времени t1 с

начальной координатой x0 и начальной скоростью, равной 0. В момент времени t1 , когда координата тела стала равна x1 , оно стало двигаться равнозамедленно (парабола bc ) и в момент времени t2 остановилось (ведь касательная mn

параллельна оси времени). Все это время тело удалялось от начала координат 0. После остановки оно начало двигаться назад, приближаясь к началу координат, сначала равноускоренно (парабола cd ) до момента времени t3 , а затем, когда его координата вновь стала равна x1 , оно начало

двигаться равнозамедленно и в момент времени t4 остановилось (касательная к параболе de в точке e ,

параллельна оси времени). Ветви параболы на графике координаты могут опускаться и ниже оси времени, поскольку координата тела может быть как положительной так и отрицательной.

График перемещения, точнее проекции перемещения rx , равнопеременного движения, имеет такой же вид, как и график координаты.

6. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ С ПЕРЕМЕННЫМ УСКОРЕНИЕМ

Назовем в общем случае переменным прямолинейным движением движение по прямолинейной траектории с переменным ускорением. Быстрота такого движения характеризуется средней скоростьюcp , которую можно определить отношением пути S ко всему времени движения t,

Если путь S состоит из N отдельных участков, на которых тело двигалось равномерно или равноускоренно, или равнозамедленно, то его можно представить в виде суммы этих участков. Тогда

Скорость в данный момент времени – это мгновенная скорость. Вектор мгновенной скорости в данный момент времени сонаправлен с вектором перемещения тела в этот момент.

Пусть в некоторый момент времени радиус-вектор, соединяющий движущееся тело с началом отсчета, был равен r , а через промежуток времени t он стал равен r r , где r – перемещение тела

7. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ И ПОКОЯ. ИНЕРЦИАЛЬНЫЕ И НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА. СЛОЖЕНИЕ СКОРОСТЕЙ. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ

Опыт убеждает нас, что одно и то же тело может находится в состоянии покоя относительно одних систем отсчета и одновременно двигаться относительно других. Космонавт, сидя в кресле взлетающей ракеты, покоится относительно системы отсчета, связанной с ракетой, и движется относительно системы отсчета, связанной стартовой площадкой. Наблюдатель на платформе может утверждать, что он покоится, а пассажир поезда, отходящего от платформы, движется вперед. Но и пассажир в поезде может утверждать то же самое, т. е. что покоится именно он, а наблюдатель на платформе движется назад. Оба они правы, потому что движение и покой относительны.

Относительность движения состоит в том, что одно и то же тело может одновременно и двигаться, и покоиться, смотря относительно какой системы отсчета рассматривается его движение.

Абсолютно покоящихся тел в природе не существует. Покой – частный случай движения.

Назовем любое тело свободным, если на него не действуют другие тела. В условиях окружающего нас мира такие тела отыскать сложно. Но можно привести множество примеров, когда действие других тел на данное тело скомпенсировано, т. е. другие тела как бы и не действуют на него. Например, на неподвижно висящую пушинку действует сопротивление воздуха и земное притяжение, но эти действия скомпенсированы и потому пушинку можно считать свободной до тех пор, пока воздушные потоки не увлекут ее. С понятием свободного тела связано одно из важнейших понятий механики – понятие инерциальной системы отсчета.

Системы отсчета, относительно которых свободное тело покоится или движется равномерно и прямолинейно, называются инерциальными. Инерциальными также являются системы отсчета, которые покоятся или движутся равномерно и прямолинейно относительно других инерциальных систем отсчета.

Инерциальной системой отсчета с большой точностью можно считать систему отсчета, в начале координат которой находится Солнце, а оси координат направлены на неподвижные относительно Солнца звезды. Если отвлечься от криволинейности траектории Земли, движущейся вокруг Солнца, то Землю так же можно считать инерциальной системой отсчета.

Системы отсчета, движущиеся с ускорением относительно инерциальных систем отсчета, называются неинерциальными.

Любые тела на криволинейной траектории движутся с ускорением, даже если их скорость по модулю не меняется. Поэтому все системы отсчета, движущиеся криволинейно, являются неинерциальными.

Любая реальная система отсчета является неинерциальной, поскольку она всегда участвует в том или ином криволинейном движении. Даже система отсчета, в которой началом отсчета служит Солнце (гелиоцентрическая система отсчета) не является абсолютно инерциальной, поскольку вращается вокруг центра Галактики. Однако ее можно считать инерциальной с высокой степенью точности.

Рассмотрим инерциальную систему отсчета X1O1Y1 которая движется относительно покоящейся инерциальной системы отсчета XOY со скоростью 0 (рис. 7-1).

Пусть в движущейся системе отсчета перемещается материальная точка M со скоростью 1 относительно этой

системы в том же, что и система X1O1Y1 , направлении. Для упрощения выводов будем считать, что векторы скоростей 0 и1 параллельны осям координат OX и O1 X1 т. е., что 0 x 0 и1x 1 .

скоростью 1 относительно стен вагона.

Пусть в начальный момент времени оси координат обеих систем отсчета совпадали, а затем за время t подвижная система отсчета прошла некоторое расстояние. Тогда координата x точки M в неподвижной системе отсчета может быть определена через координату x1 этой точки в движущейся системе и

скорость этой системы 0 по формуле

движения самой подвижной системы не изменялось бы,

y y1 .

Если бы наши инерциальные системы отсчета имели и третьи оси координат OZ, и O1Z1 то координаты Z и Z1 точки M тоже при этом условии были бы одинаковы,

z z1 .

Запишем последние три равенства вместе и будем считать само собой разумеющимся, что промежуток времени t за который пассажир прошел расстояние S , в обеих системах отсчета одинаков,

(7.1)

(7.2)

(7.3)

(7.4)

Здесь t – промежуток времени в неподвижной сситеме отсчета, промежуток времени в подвижной системе отсчета.

Система уравнений (7.1)–(7.4) позволяет осуществить переход от координат и времени в подвижной инерциальной системе отсчета к координатам и времени в неподвижной инерциальной системе отсчета при скоростях, несравненно меньших скорости света в вакууме. Эти уравнения называются

преобразованиями Галилея для координат и времени. Следовательно, координата – величина относительная.

Пусть точка M , двигаясь равномерно в направлении оси OX , за время t совершила перемещениеr1 в подвижной системе отсчета. Очевидно, что при этом сама подвижная система отсчета

Таким образом, перемещение – тоже относительная величина. В разных инерциальных системах отсчета оно различно.

Рассмотрим еще раз эти же инерциальные системы отсчета. Пусть в подвижной системе отсчета на оси O1 X1 лежит неподвижный относительно этой системы стержень AB длиной l0 (рис. 7-2). Координаты

концов этого стержня в подвижной системе x1A и x1B , в неподвижной системе координаты его концов соответственно xA и xB , а его длина в этой системе равна l. Длина стержня связана с координатами его

концов соотношениями

l0 x1B x1A и l xB xA , (7.6)

Из рис. 7-2 можно сразу сделать вывод, что l l0 . Такой же вывод можно сделать, если подставить в уравнение (7.6) преобразования Галилея для координаты x (7.1):

Выражение (7.7) называют правилом сложения скоростей в классической механике (когда скорости тел несравненно меньше скорости света в вакууме).

Правило сложения классических скоростей: скорость тела относительно неподвижной системы отсчета равна сумме скорости тела относительно подвижной системы отсчета и скорости самой подвижной системы относительно неподвижной.

Скорость , с которой тело движется относительно неподвижной системы отсчета, называются абсолютной скоростью, скорость 1 , с которой тело движется относительно подвижной системы отсчета,

называют собственной скоростью, и скорость 0 , с которой сама подвижная система отсчета движется

относительно неподвижной, называют переносной скоростью. Следуя этим терминам, правило сложения классических скоростей можно сформулировать так: абсолютная скорость равна сумме собственной и переносной скоростей.

В общем случае при разном направлении векторов скоростей , 1 и 0 правило (7.7) можно

применять только в векторном виде и переходить к скалярной записи, используя теоремы и формулы математики. Однако в случае, изображенном на рис. 7-1, когда все скорости сонаправлены, можно записать выражение (7.7) в скалярном виде:

Полезно знать, что неподвижную систему отсчета физики называют лабораторной системой, а движущуюся – собственной системой отсчета. Исходя из этих названий, правило сложения скоростей в классической механике может быть сформулировано еще и так: скорость тела относительно лабораторной системы отсчета равна сумме скорости этого тела относительно собственной системы отсчета и скорости самой собственной системы относительно лабораторной.

Приведем примеры на правило сложения классических скоростей. Пусть от Земли удаляется космический корабль со скоростью 0 , а в нем в направлении его полета от хвоста к носу перемещается

космонавт со скоростью 1 относительно корабля. Какова скорость космонавта относительно наблюдателя на Земле? Конечно, она равна сумме скорости самого космонавта относительно корабля 1 и корабля относительно Земли 0 , что соответствует уравнению (7.8). Если же космонавт движется от носа корабля к его хвосту, то его абсолютная скорость будет равна разности скоростей 0 и 1 . Таким

Сложение скоростей удовлетворяет принципу суперпозиции (независимости) движений: результат сложного движения представляет собой сумму отдельных движений, происходящих независимо друг от друга.

Принцип суперпозиции широко применяется на практике и не только в механике. Он играет большую роль в теории волновых процессов, в теории электрических цепей и в других разделах физики.

Рассмотрим пример. Пусть две материальные точки M и N движутся в неподвижной системе отсчета XOY со скоростями M и N относительно этой

системы (рис.7-4).

Определим скорость точки N относительно точки M NM .

Будем рассуждать, исходя из правила сложения скоростей. Свяжем с точкой

Следовательно, в этом случае правило сложения скоростей (7.7) запишется следующим образом:N M NM ,

откуда искомая скорость NM , т. е. скорость точки N относительно точки M будет равна:NM N M .

На рис. 7-5 показано, как можно определить скорость NM графически. Эта скорость есть векторная разность векторов N и M . Чтобы ее найти, надо соединить концы векторов M и N вектором NM , направленным от конца вычитаемого вектора M к концу уменьшаемого вектора N . Это вектор NM и есть векторная разность векторов N и M , т. е. скорость точки N относительно

точки M .

Таким образом, чтобы определить скорость второго тела относительно первого, можно, не меняя направления векторов скоростей, соединить на чертеже их начала в одной точке, а затем построить вектор, равный векторной разности уменьшаемого и вычитаемого векторов. Этот вектор должен соединять концы векторов скоростей тел и быть направлен от конца вычитаемого вектора к концу уменьшаемого. Чтобы определить модуль относительной скорости двух тел, надо, опираясь на полученный чертеж, применить теоремы и формулы геометрии и тригонометрии.

Теперь порассуждаем об ускорениях тел в разных инерциальных системах отсчета. Обратимся еще раз к рис. 7-1. Системы XOY и X1O1Y1 инерциальные, т. е. их скорости постоянны. Скорость системы

XOY равна нулю, а скорость системы X1O1Y1 равна 0 . Пусть скорость материальной точки M в системе

Получается, что изменение скорости за одно и то же время в разных системах отсчета одинаково.

Ускорение тела во всех инерциальных системах отсчета скоростях одинаково, т. е. оно абсолютно по отношению к любым инерциальным системам отсчета.

Таким образом, если ускорение тела равно нулю в одной из инерциальных систем отсчета, то оно будет равно нулю и во всех иных инерциальных системах отсчета, т. е. относительно любых инерциальных систем отсчета тело будет двигаться равномерно и прямолинейно или покоиться. При этом никакими экспериментами, проводимыми в одной из инерциальных систем отсчета, нельзя будет определить, покоится ли эта система или движется. Так, космонавты в космическом корабле, движущемся прямолинейно и равномерно относительно звезд, не смогут сказать, движутся ли они или покоятся, пока не сравнят свое положение с положением звезд.

Все эти выводы обобщает один из общих законов природы, сформулированный Галилеем и получивший название принципа относительности Галилея.

Принцип относительности Галилея: все механические явления протекают во всех инерциальных системах отсчета одинаковым образом.

Преобразования, вид которых не изменяется, если поменять одну инерциальную систему отсчета на другую, называются инвариантными.

Другая формулировка принципа относительности Галилея: все законы механики инвариантны по отношению к любым инерциальным системам отсчета.

Если же подвижная система отсчета движется относительно неподвижной с ускорением, т. е. если эти системы неинерциальны, то в уравнении (7.10) к изменению скорости 1 материальной точки M в

системе отсчета X1O1Y1 надо прибавить изменение скорости самой подвижной системы отсчета 0 ,1 0 .

Разделив все члены этого уравнения на промежуток времени t , за который произошло изменение скоростей, мы придем к правилу сложения ускорений в неинерциальных системах отсчета, движущихся прямолинейно (во вращающихся системах отсчета возникает еще и угловое ускорение):

XOY .

Правило сложения ускорений в неинерциальных системах отсчета: ускорение тела относительно неподвижной системы отсчета равно сумме ускорения этого тела относительно подвижной системы отсчета и ускорения самой подвижной системы относительно неподвижной.

Таким образом, ускорение в неинерциальных системах отсчета относительно, а в инерциальных – абсолютно.

8. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ. УСКОРЕНИЕ СВОБОДЦОГО ПАДЕНИЯ. ДВИЖЕНИЕ СВОБОДНО ПАДАЮЩЕГО ТЕЛА ПО ВЕРТИКАЛИ

Свободным падением тел называют падение тел в вакууме под действием только притяжения планеты.

Свободное падение является частным случаем равнопеременного движения – это равноускоренное движение, если тело движется вниз, и равнозамедленное, если оно свободно брошено вверх.

Ускорение g , с которым тело под действием притяжения планеты свободно падает, называется

ускорением свободного падения. Вектор ускорения свободного падения всегда направлен вниз к поверхности планеты.

Ускорение свободного падения равно изменению скорости свободно падающего тела за единицу

времени,

g 0 . t t

Одним из первых изучил свободное падение тел великий итальянский физик Галилео Галилей. Он открыл один из важнейших законов механики, получивший название закона Галилея.

Закон Галилея: все тела под действием земного притяжения падают с одинаковым ускорением.

В средних широтах Земли ускорение свободного падения равно: g = 9,8 м/с2.

Ускорение свободного падения ни зависит ни от массы, ни от формы и размеров падающего тела. В этом можно наглядно убедиться при помощи прибора, который называют трубкой Ньютона (рис. 8-1).

Трубка Ньютона представляет собой герметично закрытый стеклянный цилиндр длиной около метра, из которого выкачан воздух. В трубке находятся тела разной массы, формы и размеров: монетка, дробинка и перышко. Когда трубку располагают вертикально так, чтобы все тела оказались вверху, то они пролетают всю длину трубки за одно и тоже время, двигаясь равноускоренно без начальной скорости с одинаковым ускорением свободного падения. На малых по сравнению с радиусом Земли высотах ускорение свободного падения постоянно и не зависит от высоты тела над Землей.

Ускорение свободного падения зависит от массы, формы и размеров планеты, на которую тела падают, а также от расстояния между падающим телом и центром планеты. Эта зависимость выражается формулой:

g G M

R H 2

Здесь G = 6,67∙1011 Н∙м2/кг2 – гравитационная постоянная, M – масса планеты, R – радиус планеты, H – расстояние от тела до поверхности планеты.

Уменьшение ускорения свободного падения становится заметным на высоте, сравнимой с радиусом планеты.

Поскольку земной шар имеет форму геоида, т. е. сплюснут у полюсов, то на полюсе тело ближе к центру Земли, чем на экваторе, поэтому на полюсе оно сильнее притягивается к Земле и так ускорение свободного падения больше, чем в других точках земного шара.

Кроме сказанного, на величину ускорения свободного падения оказывает влияние суточное вращение планеты вокруг своей оси. Находясь на полюсе, тело не принимает участия в этом вращении, тогда как на экваторе радиус вращения тела вокруг земной оси наибольший, поэтому на экваторе ускорение свободного падения тел имеет наименьшую величину по сравнению с его величиной на иных широтах земного шара, а на полюсе – наибольшую. На экваторе оно равно 9,78 м/с2, а на полюсе достигает 9,83 м/с2. Величина ускорения свободного падения зависит также от плотности земных пород. В местах залегания железных руд она больше, чем там, где породы имеют меньшую плотность, из-за