44. Случайные величины и законы их распределения.

Случайная – переменная величина, значение которой зависит от случайных исходов некоторого испытания.- вероятностное пространство, тогда числовая функция от элементарного события называют случайной величиной, если каждому исходу некоторого испытания поставлено в соответствие единственное действительное число х – значение случайной величины на . Х- случайная величина, . Случайная величина считается заданной, если задан закон ее распределения, т.е. мн-во зн-й и соотв. вероятности. Закон распределения – соотв м/д зн-ми случ вел и соотв вероятностями. Величины: дискретные, непрерывные. Осн ф-и: ряд распределения (д/Д), плотность распределения вероятности (д/Н), ф-я распределения (д/Д,Н). Функция, ставящая в соответствие каждому действительному числу х вероятность того, что значение случайной величины Х меньше этого числа – функция распределения случайной величины Х. F(x)=P(X<x). Свойства 1. 2. 3. Монотонно- неубывающая F(x). 4. 5. Непрерывна слева F(x), т.е. F(x)=F(x-0). Th. Пусть дана функция F(x) – определенная на всей числовой оси и удовлетворяющая свойствам 3,4,5, тогда существует единственная случайная величина x, для которой F(x) – функция распределения. Дискретная сл. величина – случайная величина , множество значений которой конечно или счетно.

Закон распределения ДСВ можно представить: 1) таблица Х – ДСВ, - значения величины, i=1,2,…,n и вероятности Будем считать, что все -различны, тогда

Х			…
			…

Таблица распределения ДСВ Х – ряд распределения. Th. . 2)Аналитически. 3) Графически. В декартовой системе координат отмечают точки , соединяют их последовательно отрезками прямой, получается ломаная – многоугольник распределения вероятности случайной величины. Для ДСВ функция распределения ступенчатая. Основные законы распределения ДСВ. 1) Равномерное распределение. ДСВ x имеет равномерный закон распределения, если все значения принимаются с равными вероятностями . 2) Биномиальный закон распределения. ДСВ х имеет биномиальный закон распределения, если она принимает значения 0,1,…,n. - вероятность, гдеq=1-p, k=0,…,n.

- бином Ньютона.

	0	1	2	…	n

Замечание. Биномиальный закон распределения применим при небольших n, вероятность его в (0;1). 3) Закон распределения Пуассона. ДСВ х имеет закон распределения Пуассона х=0,1,2,…,k – может быть , но множество значений счетно с вероятностью ,

k=0,1,2,…

	0	1	2	…	k

Замечание. При достаточно больших n () и малых вероятностях и условии, что np= const закон распределения Пуассона хорошо приближает биномиальный закон распределения, иначе является его предельным случаем. 4) Геометрическое распределение. ДСВ х имеет геометрический закон распределения, если х=1,2,…,k…, ( , но множество значений счетно) с вероятностью .

Испытания заканчиваются как только наступает событие А.

	1	2	3	…	k
	p	qp		…

Непрерывная случайная величина - случайная величина х, множество значений которой есть некоторый числовой промежуток. Случайная величина Х – функция распределения которой непрерывна в каждой точке и дифференцируема всюду наз непрерывная. Плотность распределения вер-ти. Пусть Х – случайная величина и F(x) – ee функция распределения непрерывна и дифференцируема в каждой точке числовой оси, тогда из свойств функции распределения можем записать попадание случайной величины в промежуток Р

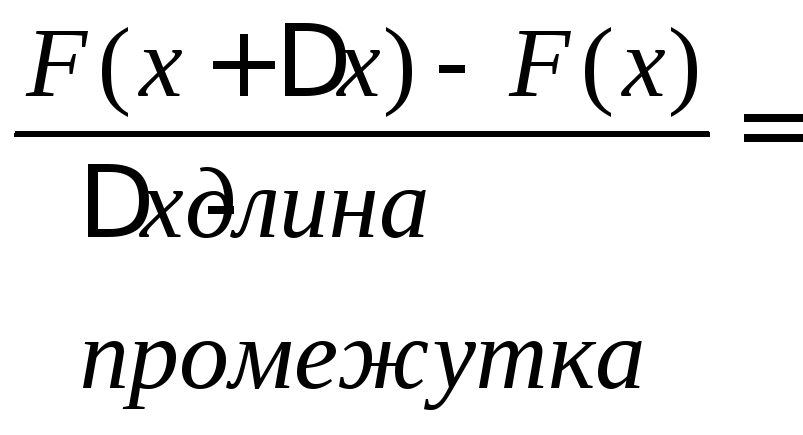средняя вероятность, приходящаяся на 1 длины данного промежутка.

В силу непрерывности F(x) можно перейти к пределу

- плотность распределения вероятности. График Y=f(x) наз кривой распределения вер-ти. Плотность – диф з-н распределения. Th. Вероятностное попадание некоторой случайной величины в = значению интеграла от плотности распределения вероятности . Геометрически вероятность того, что непрерывная случайная величина примет значения =S криволинейная трапеция, ограниченная осью 0Х, прямыми х=а, х=b, кривой распределения y=f(x).Зная плотность распределения вероятности можно найти функцию распределения .

Св-ва плотности распределения: 1) f(x)>=0. Геом. – все т кр расп лежат не ниже оси OX. 2) интеграл от - до + f(x)dx=1. Геом. Площадь криволин трапеции огранич OX и кр распр=1. Св-ва непр сл в: 1) Если сл в x имеет плотность распределения, то ее ф-я распред явл непр. 2) Во всякой т сущ плотность распред вер-ти. 3) Вер-ть каж отд зн-я непрер с в =0. Th. Если с в имеет плотность распределения вер-ти, то она явл непрер, но не всякая непрер сл в имеет пл-ть распр вер-ти. Необх усл-м сущест плотности распр вер-ти явл непрер ф-и распр. Дост явл непрерывность F(x), f(x) за исключением конечного числа точек. Виды распределений НСВ: 1)Равномерное распределение. Распределение вероятности непрерывной случайной величины Х- равномерное, если на всем промежутке, которому принадлежит значение Х, плотность распределения вероятности сохраняет постоянное значение.

Пусть Х –НСВ (а,b) f(x) – const

2)Показательное распределение. Показательным распределением непрерывной случайной величины Х, которое описывается плотностью

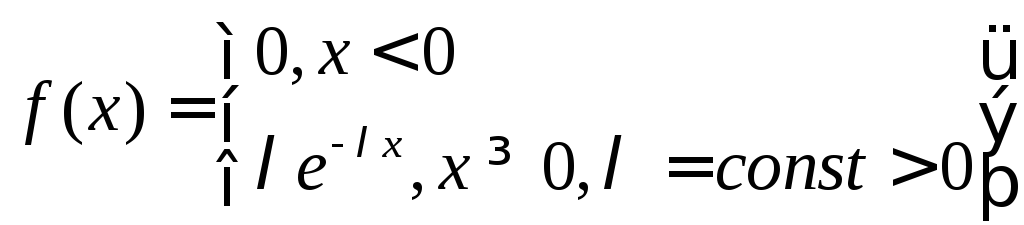Функция распределения

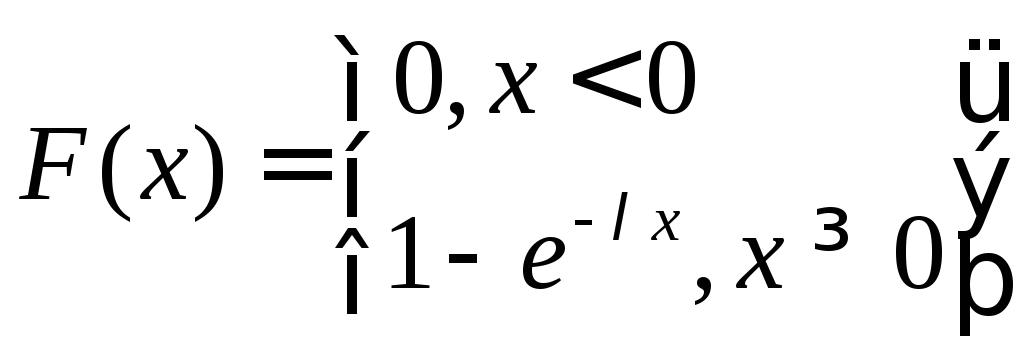
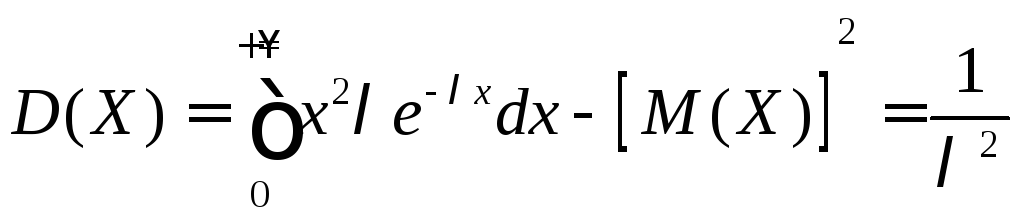
3)Нормальное распределение. Распределение вероятности нсв, плотность которой задается функцией 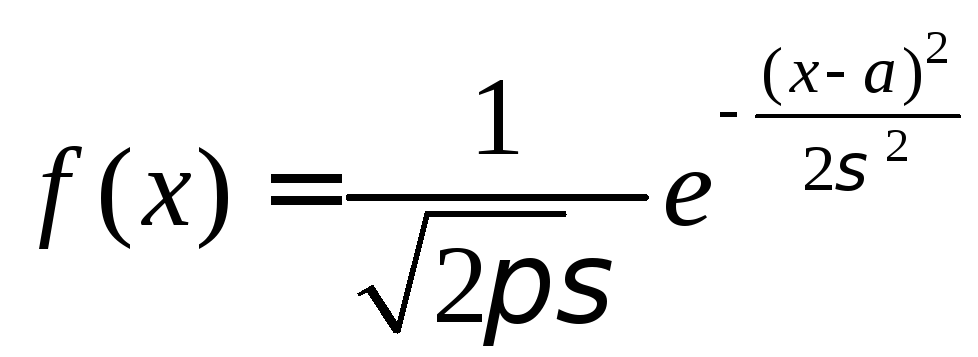- нормальное (Гаусовское),

, если а=0, , то нормальное распределение стандартное

Th. Для нормально распределенной случайной величины а – М(х), - среднеквадратичное отклонение. Ассиметрия , Эксцесс