43. Вероятность случайного события. Основные свойства вероятности.

Случайное событие - исход какого-либо испытания, которое может произойти или нет. Исходы испытания принято называть элементарными событиями. Событие называется достоверным, если оно всегда происходит в данном испытании. Событие, кот.никогда не происходит в данном испытании называется невозможным. События наз-ся несовместными, если наступление одного в данном испытании исключает наступление другого, если не исключает – совместными.

- алгебра событий. Множество исходов пространство элементарных событий . Класс подмножества пространства называется алгеброй множеств, если: 1. , ; 2. ; 3. . Алгебра множеств называется - алгеброй, если из того, что для . (их объединения и пересечения принадлежат этому классу)

Вероятностное пространство. Совокупность прост-ва элем.событий, сигма-алгебры и числовой функции, определенной на событиях сигма-алгебры называемой вероятностью образуют вероятностное пространство, если выполняются следующие аксиомы: 1. неотрицательность: ; 2. нормированность: ; 3. аддитивность (для несовместных): ; 4. непрерывность: .

Конечные вероятностные пространства, определение вероятности и ее свойства.

-конечно, состоит из конечного числа элементарных событий.

Вероятностью события А называется число равное отношению числа благоприятствующих исходов данного события к общему числу исходов данного испытания. m-число благоприятствующих исходов; n – общее число исходов.

Свойства вероятности:

1.; 2. ; 3. ; 4. ;

5. Теорема сложения вероятностей (расширенная теорема). Для любых событий и вероятность их суммы = сумме их вероятностей без вероятности совмещения. . Доказательство: - число исходов, благоприят. событию ; - число исходов, благоприят. событию ; ; - число исходов, благоприят. и и . чтд.

Следствие 1. Для любых несовместных событий и вероятность их суммы = сумме их вероятностей .

Следствие 2 . Для конечного числа попарно несовместных событий вероятность их суммы = сумме их вероятностей. .

Следствие 3. Если событие - есть сумма всех элементарных событий, то вероятность этих событий = 1.

6. .

Условная вероятность.

События и называются зависимыми, если вероятность одного из них зависит от того, наступило ли или нет другое событие. Вероятность события при условии наступления события называется условной вероятностью . Обоз. . Если событие фиксировано, то условная вероятность образует вероятностное пространство, в котором выполняются все аксиомы.

Теорема умножения 1. (для зависимых событий). Вероятность произведения 2-х зависимых событий равна произведению вероятности одного события на условную вероятность другого. .

События и называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другого события.

Теорема умножения 2. (для независимых событий). Вероятность произведения 2-х независимых событий равна произведению вероятностей. .

Формула полной вероятности. Совокупность событий называется конечным разбиением, если они попарно несовместны и в сумме образуют пространство элементарных событий. Теорема полной вероятности. Пусть образуют разбиение . Известна их вероятность до опыта . Тогда . Доказательство. Т.к. образуют разбиение, то они попарно несовместны. А поскольку наступает с одним из этих событий, то можно сказать, что наступает с их суммой . =. Из того, что несовместны следует, что несовместны, тогда . Чтд. - гипотезы (предположения).

Формула Байеса. Формула Байеса дают возможность «пересмотреть» вероятности гипотез с учетом результатов проведенных испытаний. Теорема гипотез. Пусть образуют разбиение , . Известны их вероятности до опыта и в результате произведенного испытания наступило событие , тогда вероятность гипотезы: .

Независимые испытания Бернулли. Под испытанием мы понимаем некоторый эксперимент, исходами которого служит те или иные случайные события. Испытание – это некоторое вероятностное пространство. n – испытаний называются независимыми, если результат каждого из них не зависит от того, что произошло в других испытаниях. Частным случаем независимых испытаний является испытание с 2-мя исходами в каждом, т.е. либо наступает событие , либо не наступает. , - наступило , - наступило .

, , тогда в прямом произведении n – независимых испытаний : , . Такая схема называется схемой Бернулли.

- формула Бернулли. Если ; . Эти формулы – биномиальное распределение вероятности.

Предельные теоремы.1. Если в задаче необходимо определить вероятность того, что событие является не более и не менее какого-то числа раз, то используя теорему сложения получаем: а) не более m раз: ; b) менее m раз: ; с) более m раз: ; d) не менее m раз: .

2. Если в задаче необходимо определить вероятность того, что событие наступает число раз, заключенное в промежутке и , то используя теорему сложения получаем: .

3. Наиболее вероятностное число наступления событияв n – независимых испытаниях заключено в промежутке . А) - целое число, то ; б) - нецелое число , то .

Локальная теорема Муавра – Лапласа. Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, а число испытаний достаточно велико, то вероятность того, что событие наступает ровно к – раз в n – независимых испытаниях: , где .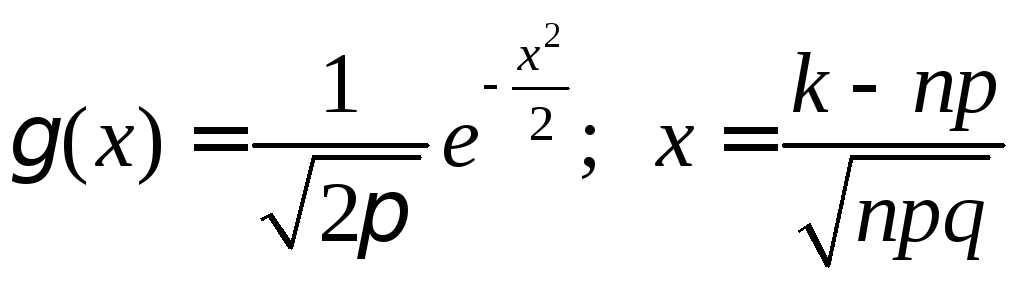

Формула Пуассона. Если вероятность наступления события в каждом испытании постоянна и мала, а - велико, но остается не больше , то вероятность того, что событие наступает ровно к – раз: .

Интегральная теорема Муавра – Лапласа. Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, а - велико, то вероятность того, что событие в n – независимых испытаниях состоится число раз, заключенная в промежутке от до : . ; .

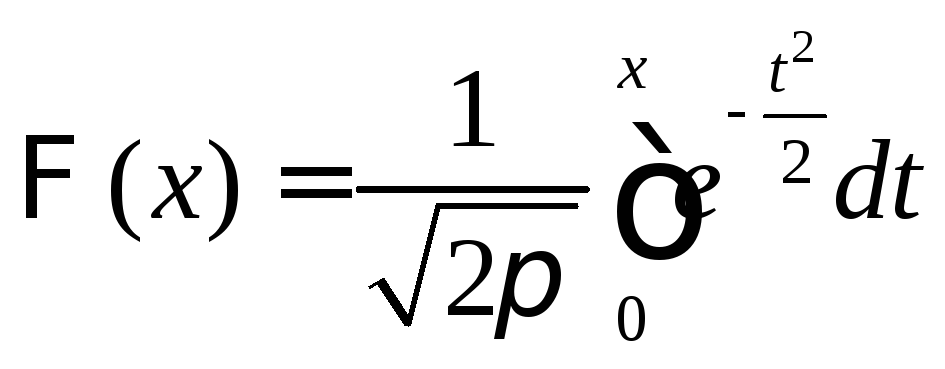Следствие 1: Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, а - велико, то вероятность того, что событие в n – независимых испытаниях отклонятся по абсолютной величине от не более, чем на некот. положение : . Следствие 2: Если вероятность наступления события в каждом испытании постоянна и отлична от 0 и 1, а - велико, то вероятность того, что в n – независимых испытаниях абсолютная величина отклонения относительно частоты события от ее вероятности наступления не превзойдет некоторого положительного : .