Уравнение прямой

1. Уравнение прямой, заданной точкой и направляющим вектором

Пусть на плоскости выбрана аффинная система координат и пусть в этой системе известны координаты некоторой точки прямой и направляющего вектора этой прямой (рис. 3). Напишем уравнение прямой d. Очевидно, точка лежит на прямой d тогда и только тогда, когда векторы и коллинеарны. Так как вектор имеет координаты то по теореме:

Векторы и коллинеарны тогда и только тогда , когда

(1)

Если точка M лежит на прямой d, то ее координаты удовлетворяют уравнению (1), а если она не лежит на прямой, то ее координаты не удовлетворяют этому уравнению, поэтому уравнение (1) является уравнением прямой d. Уравнение (1) можно также записать в виде: (1^/)

2. Уравнение прямой, заданной двумя точками

(2)

3. Уравнение прямой с угловыми коэффициентами

Пусть на плоскости выбрана аффинная система координат и дана прямая d, пересекающая ось ординат. Если - направляющий вектор прямой, то и не коллинеарны, поэтому .Число называется угловым коэффициентом прямой d.

Угловой коэффициент k имеет простой геометрический смысл, если прямая задана в прямоугольной системе координат . В самом деле, пусть - направляющий вектор этой прямой (см. рис.).

где . Следовательно,

Таким образом, число k позволяет определить угол

, поэтому k называется угловым коэффициентом прямой.

Составим уравнение прямой, заданной в аффинной системе координат точкой и угловым коэффициентом k. Пусть -направляющий вектор прямой. Тогда согласно формуле (1^/) уравнение прямой имеет вид: или, разделив на а₁, получаем: (3) Если в качестве точки взять точку пересечения прямой d с осью ординат, то уравнение (3) примет вид:

(4) Это уравнение называется уравнением прямой с угловым коэффициентом. В виде (4) можно записать уравнение любой прямой, пересекающей ось ординат.

4. Параметрическое уравнение прямой

Выберем какую-нибудь аффинную систему координат и зададим прямую d направляющим вектором и точкой .Точка принадлежит прямой тогда и только тогда, когда , т. е. когда существует такое число t, что . Это соотношение в координатах запишется так: или (5) Эти равенства называются параметрическими уравнениями прямой, а t ее параметром.

Общее уравнение прямой

Теорема 1. Линия на плоскости, заданная в аффинной системе координат уравнением первой степени

Ax+By+C=0, (1)

Есть прямая. Вектор (-В, А)является направляющим вектором этой прямой.

Любая алгебраическая линия первого порядка есть прямая линия. Уравнение (1) – общее уравнение прямой, а x и y-текущие координаты точки прямой.

Теорема 2. Если в аффинной системе координат прямая d задана уравнением (1), то полуплоскости с границей d определяются неравенствами: Ax+By+C<0, Ax+By+C>0.

Расстояние от точки до прямой

Пусть - точка, не лежащая на прямой d.Дина перпендикуляра проведенного из точки к прямой d, называется расстоянием от точки до прямой d:

(2)

Общее уравнение линии второго порядка

В аффинной системе координат общее уравнение линии второго порядка имеет вид:

(1)

Коэффициенты – любые действ. числа, не равны одновременно нулю.

Пусть

Уравнение (1) можно записать в виде: или

(2)

Уравнение прямой в пространстве

Пусть d – прямая в пространстве. Любой ненулевой вектор, параллельный этой прямой, называется ее направляющим вектором. Все эти векторы, вместе с нулевым вектором, образуют одномерное векторное подпространство, которое называется направляющим подпространством прямой d.

1. Каноническое уравнение прямой. Пусть в пространстве выбрана аффинная система координат и в этой системе известны координаты некоторой точки 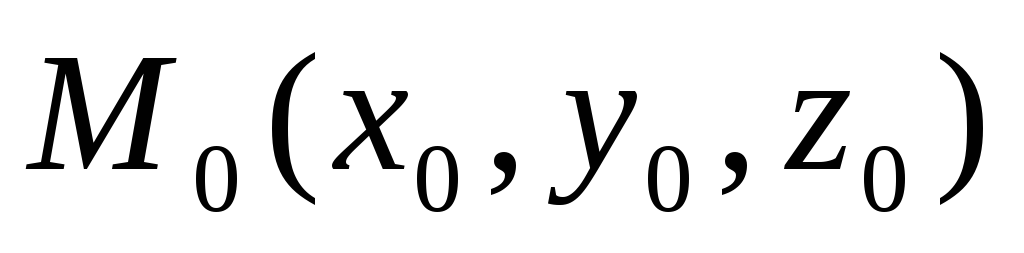и координаты направляющего вектора 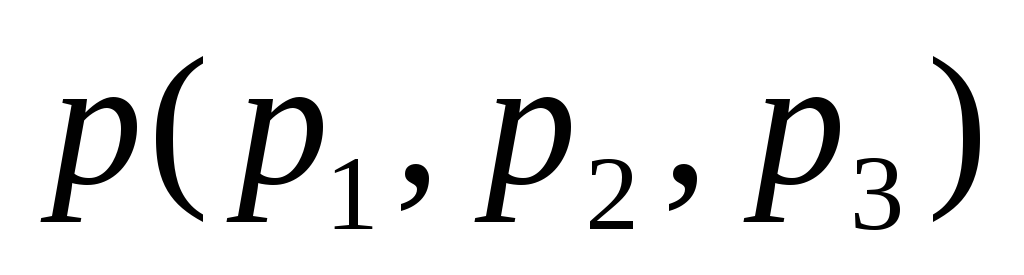прямой d. Условие коллинеарност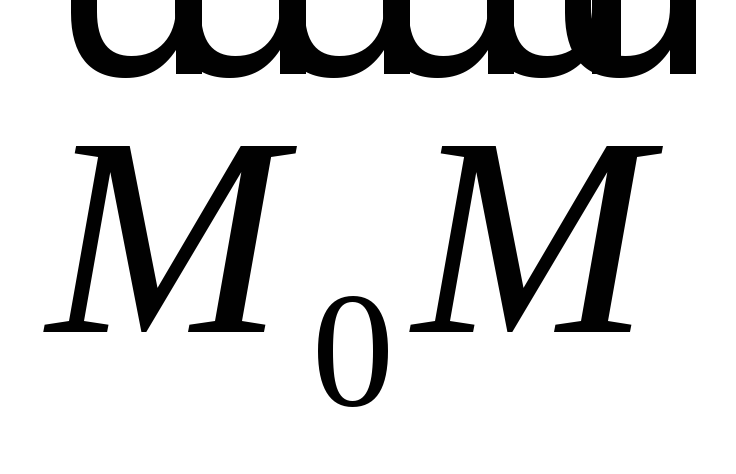и и 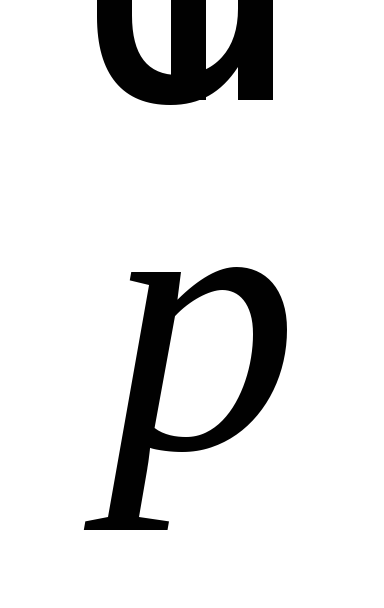запишется так:

(1) – уравнение прямой d.

(2) – .

, (3) - прямая d параллельна оси Ox.

Уравнения (1) , (2), (3) называются каноническими уравнениями прямой.

2. Уравнение прямой, заданной двумя точками.

(4)

3. Уравнение прямой, заданной двумя плоскостями. Пусть прямая d является линией пересечения плоскостей 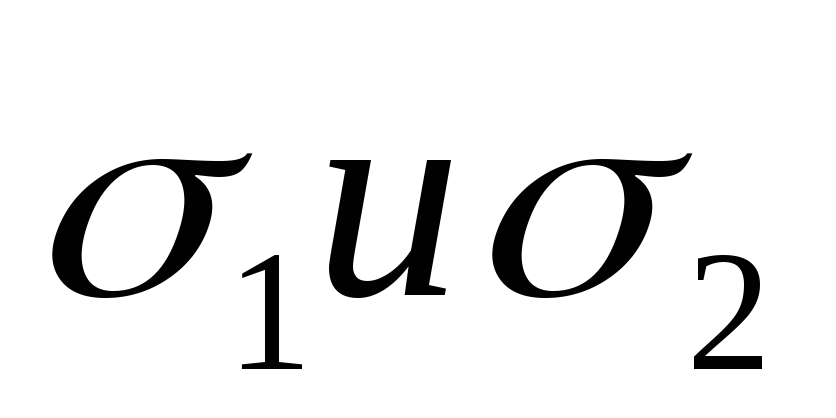, которые в аффинной системе координат заданы уравнениями: 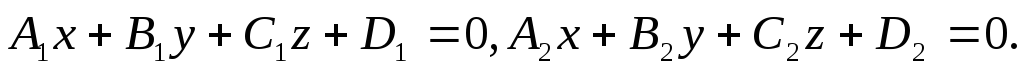(5) Точка 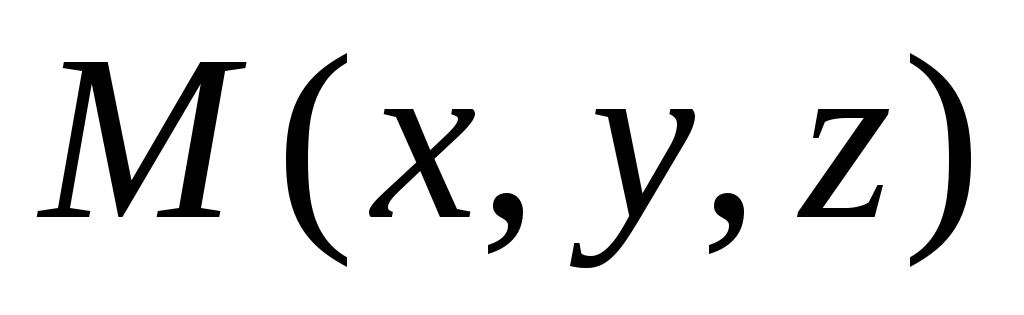лежит на прямой d, тогда и только тогда, когда ее координаты являются решением системы уравнений (5), поэтому эта система и является уравнениями прямой d. Обратно, любая система уравнений (5) представляет собой уравнения некоторой прямой пространства, если ранг матрицы 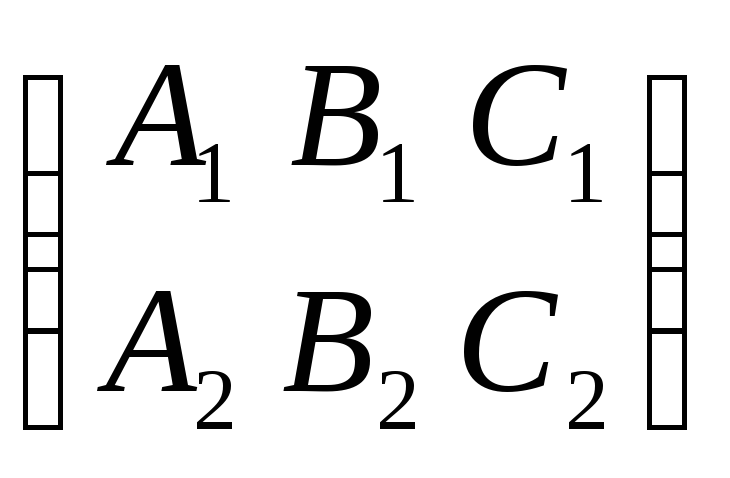равен двум. Лемма. Если в аффинной системе координат прямая, заданная уравнениями (5), то вектор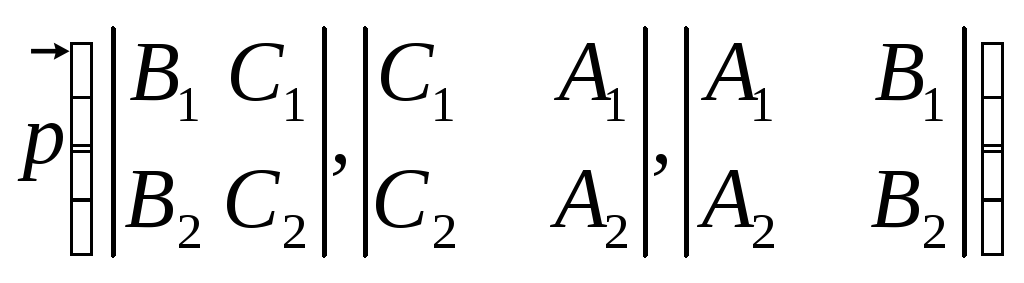является направляющим вектором этой прямой.

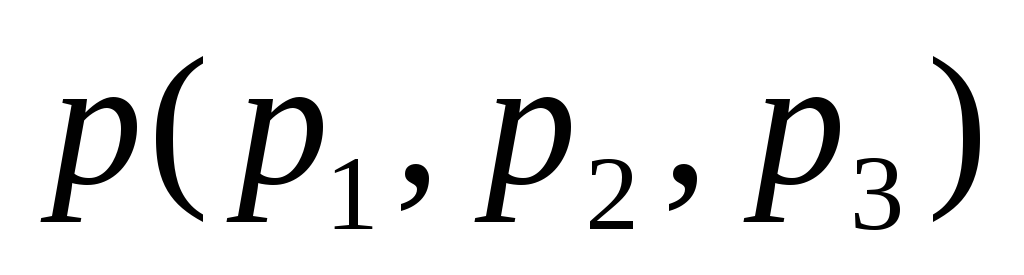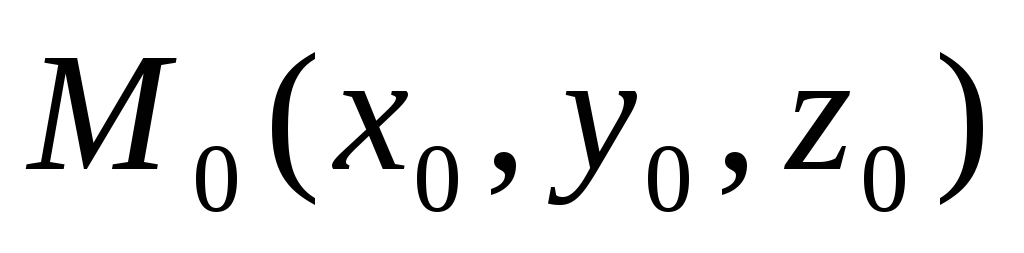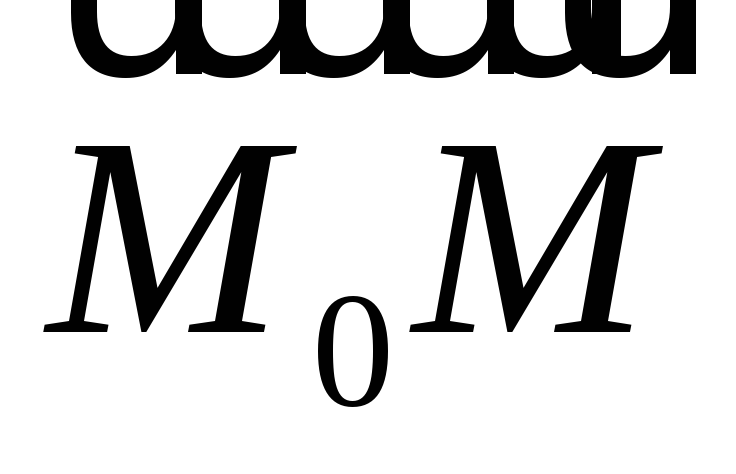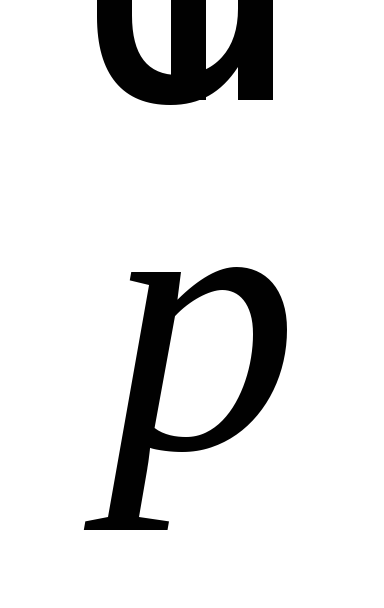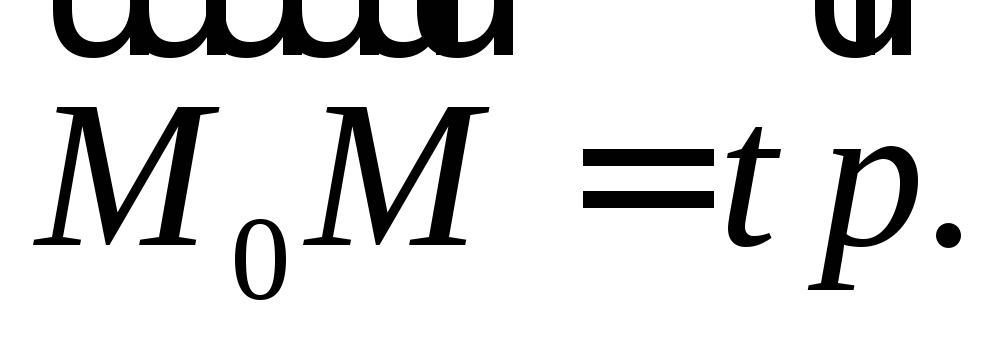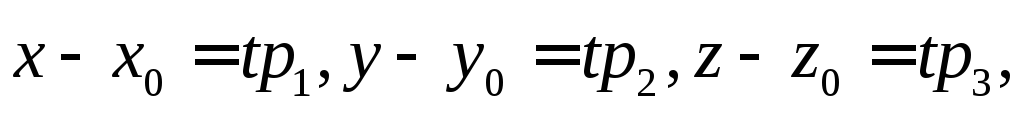4. Параметрическое уравнение прямой. Пусть в пространстве выбрана аффинная система координат и зададим прямую d направляющим вектороми точкой . Точка M(x,y,z) пространства лежит на прямой d тогда и только тогда, когда векторы и коллинеарны, т. е. когда существует такое число t, что Это соотношение в координатах запишется: или

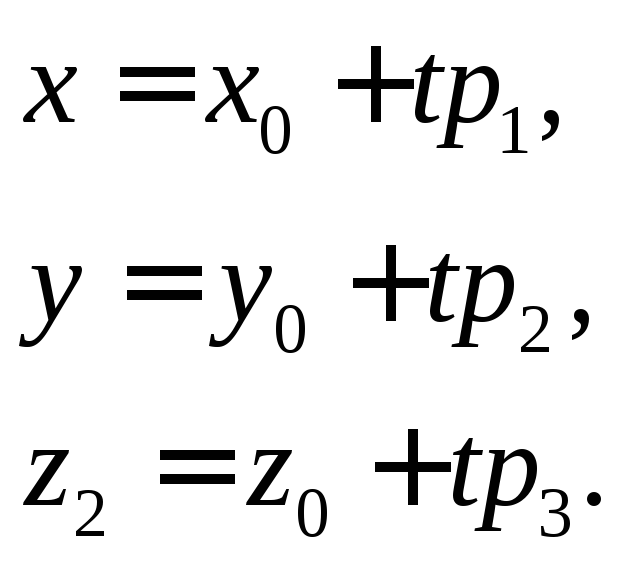
Эти равенства называются параметрическими уравнениями прямой, а t – параметром.