
Lineynaya algebra i analitich_geom / Kuznecova_s_n_lukin_m_v_lineynaya_algebra_i_analiticheskaya
.pdf
ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
Отрезок AB , где A(x1, y1 ), B |
(x2 , y2 ) разделим в заданном отношении |
|||||
λ > 0 .uuuur |
uuur |
uuuur |
uur |
|||
AM |
= λMB , но |
AM =(x − x1, |
y − y1 ), а MB =(x2 − x, y2 − y). |
|||
Учитывая, что равные векторы имеют равные координаты, получим |
||||||
x − x1 = λx2 −λx и y − y1 = λy2 −λy , |
||||||
Т.е. |
x = |
x1 +λx2 |
, y = |
y1 +λy2 |
. |
|
1+λ |
|
|
||||
|
|
|
1+λ |
|
||
ЛИНИИ НА ПЛОСКОСТИ
Введение системы координат позволяет определить положение точки плоскости заданием двух чисел, а положение линии на плоскости определяет уравнение, т.е. равенство, связывающее координаты точек.
Уравнением линии на плоскости Oxy называется такое уравнение F (x, y)= 0 с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки, не
лежащей на этой линии.
Уравнение линии позволяет изучение геометрических свойств линии заменить исследованием ее уравнения.
Уравнение F (r,ϕ)= 0 называется уравнением линии в полярной
системе координат.
Линию на плоскости можно задать при помощи двух уравнений
(параметрическое уравнение):
x = x(t )
y = y(t ), где x и y — координаты произвольной точки, а t —
переменная называемая параметром.
Линию на плоскости можно задать векторным уравнением: rr = rr(t ). При изменении параметра конец вектора r опишет некоторую линию.
УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ
Положение прямой на плоскости однозначно определяется ординатой точки N (0,b) пересечения с осью Oy и углом α между осью
Ox и прямой: tgα = y −x b . Обозначив k = tgα , получим уравнение прямой
с угловым коэффициентом y = kx +b .
Если прямая параллельна оси Ox , то α = 0 и k = tgα = 0. Уравнение примет вид y =b .
51

Если прямая параллельна оси Oy , то α = π2 и tgα не существует.
Уравнение примет вид x = a .
Рассмотрим уравнение первой степени относительно x и y в общем виде Ax + By +C = 0 . Покажем, что это уравнение прямой на плоскости.
Если B = 0, уравнение имеет вид Ax +C = 0 , т.е. x = −C . Это прямая |
||||
|
|
A |
|
|
параллельная оси Oy . Если B ≠ 0 , то получим y = − |
A |
x − C |
уравнение |
|
B |
||||
|
B |
|
||
прямой с угловым коэффициентом tgα = − BA .
Уравнение Ax + By +C = 0 называют общим уравнением прямой.
Некоторые частные случаи общего уравнения прямой:
1. Если A = 0, то уравнение имеет вид y = −C B . Это уравнение прямой, параллельной оси Ox ;
B . Это уравнение прямой, параллельной оси Ox ;
2.Если B = 0, то прямая параллельна оси Oy ;
3.Если C = 0 , то прямая проходит через начало координат.
Уравнение прямой, проходящей через точку M0 (x0 , y0 )
перпендикулярно ненулевому вектору, nr =(A, B) |
получим, если запишем |
|||||||
|
|
|
|
|
nr =(A, B) и |
uuuur |
|
|
условие перпендикулярности векторов |
M0M , где |
точка |
||||||
M (x, y) произвольная точка прямой. |
|
|
|
|
||||
r |
uuuuur |
A(x − x )+ B(y − y )= 0 . |
Это |
уравнение |
можно |
|||
n |
M |
0 |
M = 0 или |
|||||
|
|
|
0 |
0 |
|
|
|
|
переписать в виде Ax + By +C = 0 , где C = −Ax0 − By0 .
Уравнение прямой проходящей через две точки известно из школы:
x − x1 |
|
= |
|
y − y1 |
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
− x |
|
|
y |
2 |
− y |
|
|
|
|
|
|
|
|
|||
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
Если прямая пересекает ось Ox в точке M1 (a,0), а ось Oy в точке |
|||||||||||||||
M2 (0,b). |
|
В |
этом случае |
x −a |
= |
y −0 |
, т.е. |
x |
+ |
y |
=1. Оно называется |
||||||
|
0 −a |
b −0 |
a |
b |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнением прямой в отрезках.
52

ПРЯМАЯ НА ПЛОСКОСТИ. ОСНОВНЫЕ ЗАДАЧИ
Пусть прямые заданы уравнениями с угловыми коэффициентами y = k1x +b1 и y = k2 x +b2 . Найдем угол ϕ , на который надо повернуть одну прямую вокруг точки их пересечения до совпадения с другой прямой.
y
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α1 |
|
α2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
O |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Имеем α2 =ϕ +α1 |
(внешний угол треугольника) или ϕ =α2 −α1 . |
|
|||||||||||||||||||
|
|
Тогда tgϕ = tg(α2 −α1 )= |
|
|
tgα2 − tgα1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
+ tgα1 tgα2 |
|
|
|
|
k2 −k1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
или с учетом k1 = tgα1,k2 = tgα2 , получим tgϕ = |
|
|
|
. |
|
|
|||||||||||||||||
1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ k |
k |
2 |
|
|
|
||||
|
|
Если прямые параллельны, то k1 = k2 . |
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Если прямые перпендикулярны, то k1 k2 = −1. |
|
A1x + B1 y +C1 = 0 |
|
||||||||||||||||||
|
|
Если |
прямые |
|
заданы |
уравнениями |
|
и |
|||||||||||||||
A2 x + B2 y +C2 = 0 , |
то |
условие |
перпендикулярности |
запишется |
|||||||||||||||||||
A A + B B = 0 . А условие параллельности |
A1 |
= |
B1 |
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
A2 |
|
|
|
B2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
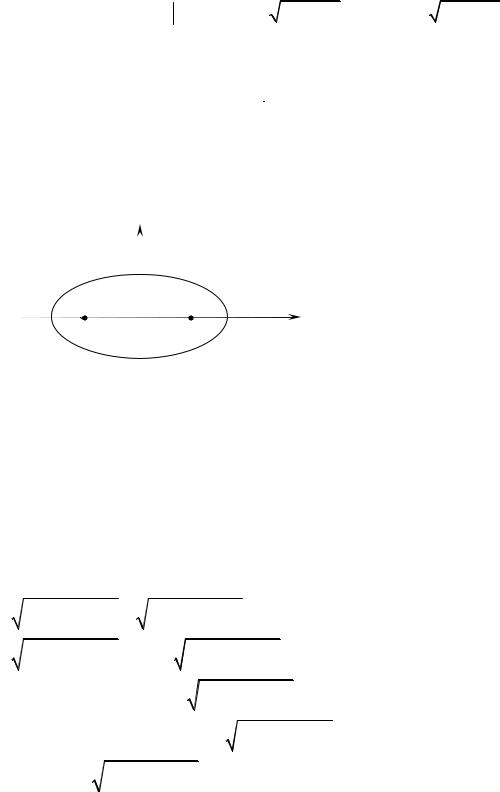
Найдем расстояние от точки M0 (x0 , y0 ) |
до прямой Ax + By +C = 0 . |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uuuuur |
|
|
|
|
Расстояние d |
равно модулю проекции вектора MM0 , где M |
||||||||||||||||||||
произвольная |
точка |
прямой |
на |
направление |
нормального вектора |
||||||||||||||||||
nr =(A, B). Т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y M1
M  d n
d n
O |
x |
53
|
uuuuur |
|
uuuuur |
nr |
|
(x0 |
− x)A +(y0 |
− y)B |
|
|
Ax0 |
+ By0 |
+C |
|
||
|
|
MM |
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||
d = |
прnr MM0 |
= |
|
r0 |
|
|
= |
|
|
|
= |
|
|
|
|
, т.к. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
n |
|
|
|
|
A2 + B2 |
|
|
|
|
A2 + B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M принадлежит прямой и Ax + By +C = 0
ЛИНИИ ВТОРОГО ПОРЯДКА
Эллипсом называется множество точек на плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (равная 2a, a > 0), большая, чем расстояние между фокусами
( 2c ).
y
|
b |
|
|
|
F1 |
|
F2 |
|
|
−a −c |
O |
c |
a |
x |
|
−b |
|
|
|
Проведем ось Ox через фокусы эллипса, от F1 до F2 . Начало |
|||||||||
координат возьмем в середине отрезка F1F2 . Фокусы имеют координаты |
|||||||||
F1 (−c,0), F2 (c,0). |
|
|
|
|
|
|
|
|
принадлежит эллипсу, векторы rr1 и r2 |
Пусть точка M (x, y) |
|
||||||||
называются ее фокальными радиус-векторами. |
|||||||||
По определению |
|
rr1 |
|
+ |
|
rr2 |
|
= 2a , отсюда |
|
|
|
|
|
||||||
(x +c)2 + y2 |
+ (x −c)2 + y2 = 2a |
||||||||
(x +c)2 + y2 |
= 2a − (x −c)2 + y2 |
||||||||
(x +c)2 + y2 = 4a2 −4a |
(x −c)2 + y2 +(x −c)2 + y2 |
||||||||
x2 + 2xc + c2 + y2 = 4a2 −4a (x −c)2 + y2 + x2 −2xc + c2 + y2
xc −a2 = a (x −c)2 + y2
x2c2 − 2xa2c + a4 = a2 x2 −2a2 xc + a2c2 + a2 y2 (a2 −c2 )x2 + a2 y2 = a2 (a2 −c2 )
54

Обозначив a2 −c2 =b2 , получим каноническое уравнение эллипса
x2 |
+ |
y2 |
=1. |
|
|
a2 |
|
|
|
||
|
b2 |
|
A1 (−a,0), A2 (a,0), |
||
|
|
Эллипс пересекает координатные оси в точках |
|||
B1 (0,b), B2 |
(0,−b) которые называются вершинами |
эллипса. Отрезки |
|||
A1 A2 = 2a, B1B2 = 2b называются большой и малой осями эллипса. Эллипс
симметричен относительно осей координат и начала координат. Форму эллипса можно охарактеризовать с помощью эксцентриситета
ε = ac (0 <ε <1). Чем больше эксцентриситет, тем более вытянут вдоль оси
Ox эллипс. Если ε = 0, то эллипс превращается в окружность. Гиперболой называется множество точек на плоскости, модуль
разности расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (равная 2a, a > 0), меньшая, чем расстояние между фокусами.
Проведем ось Ox через фокусы гиперболы. Начало координат возьмем в середине отрезка F1F2 . Фокусы имеют координаты F1 (−c,0),
F2 (c,0).
y = − b x y |
y = b x |
a |
a |
F1 |
A1 |
A2 |
F2 |
|
−c |
−a O |
a |
c |
x |
|
|
|
|
|
|
Пусть |
точка M (x, y) |
принадлежит гиперболе, в силу определения |
||||||||
гиперболы |
для фокальных радиус-векторов r1 и |
rr2 |
выполняется |
|||||||||||||
|
|
rr1 |
|
− |
|
rr2 |
|
|
|
= 2a . Выполним |
аналогичные преобразования |
и |
обозначив |
|||
|
|
|
|
|
|
|||||||||||
c2 −a2 =b2 , получим каноническое уравнение гиперболы |
x2 |
− |
y2 |
=1. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
Гипербола симметрична относительно осей координат и начала координат, состоит из двух веток, которые пересекаются с осью Ox в
55

точках A1 (−a,0), A2 (a,0), которые называются вершинами гиперболы.
Отрезок |
|
A1 A2 |
|
= 2a |
называется |
вещественной |
осью. |
Точки |
||||
|
|
|||||||||||
|
B1 (0,b), B2 (0,−b) |
|
называются |
мнимыми вершинами гиперболы, |
отрезок |
|||||||
|
B1B2 |
|
= 2b |
называют |
мнимой |
осью. |
Форму гиперболы |
характеризует |
||||
|
|
|||||||||||
эксцентриситет ε = ac . Ясно, что ε >1, причем, чем ближе он к единице,
тем сильнее ветви гиперболы прижаты к оси Ox .
Гипербола имеет асимптоты y = ± ba x .
Кривая |
определяемая |
уравнением |
y2 |
|
− |
x2 |
|
=1 |
гипербола |
||||||||
b2 |
a2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
симметричная относительно оси Ox . Гиперболы |
|
x2 |
|
− |
y2 |
|
=1 и |
y2 |
− |
x2 |
=1, |
||||||
|
a2 |
|
b2 |
|
b2 |
a2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
имеющие общие асимптоты называются сопряженными.
Параболой называется множество точек на плоскости, равноудаленных от данной прямой, называемой директрисой параболы и от данной точки, называемых фокусом.
Проведем ось Ox через фокус перпендикулярно директрисе. Расстояние от директрисы до фокуса обозначим через p и назовем его
параметром параболы. Начало координат возьмем в середине отрезка, соединяющего фокус с директрисой. Опустим из точки M (x, y) на
параболе перпендикуляр на директрису. Пусть его основание точка N ,
|
uuuur |
|
|
|
uuuur |
|
|
|
|
p 2 |
|
p 2 |
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|||||||||||||
тогда |
NM |
|
= |
|
FM |
|
, откуда следует |
x + |
|
|
= x − |
|
|
|
+ y |
|
y |
|
= 2 px . |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Имеем каноническое уравнение параболы y2 = 2 px |
|
|
|
|
|
|
|
|||||||||||||
Парабола симметрична |
относительно оси Ox |
|
и |
проходит |
через |
|||||||||||||||
начало координат.
y
|
N |
y |
M |
|
|
|
|
|
|
|
|
|
F |
− |
p |
O |
x |
p |
x |
|
2 |
|
2 |
||||
56

Уравнения y2 = −2 px , x2 = 2qy и x2 = −2qy также определяют параболы.
Рассмотренные выше кривые второго порядка имеют канонические уравнения только относительно специально подобранных систем координат. В произвольной системе координат уравнение второго порядка имеет вид
a11x2 + 2a12 xy + a22 y2 + 2b1x + 2b2 y +c = 0
Это общее уравнение кривой второго порядка.
Привести его к каноническому виду можно с помощью преобразований координат, причем вид кривой можно определить сразу, вычислив определитель
= a11 a12 a21 a22
Если > 0 , то кривая эллиптического типа. Если < 0 , то кривая гиперболического типа. Если = 0 , то кривая параболического типа.
Возможны и другие, так называемые, вырожденные случаи: для эллипса в точку, для гиперболы в пару пересекающихся прямых, для параболы в пару параллельных прямых.
Поворот осей позволяет избавиться от слагаемого, содержащего произведение xy, а параллельный перенос от слагаемых, содержащих x и y.
ТЕМА VI. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
ПЛОСКОСТЬ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Пусть в пространстве плоскость Q задана точкой M0 (x0 , y0 , z0 ) и вектором nr =(A, B,C ), перпендикулярным этой плоскости. Выведем
уравнение этой плоскости. Возьмем на ней произвольную точку M (x, y, z) |
|||||||||||
и составим вектор |
uuuuur |
− y0 |
, z − z0 ). При любом расположении |
||||||||
M0M =(x − x0 , y |
|||||||||||
точки M (x, y, z) |
|
|
|
Q |
векторы n |
uuuuur |
|||||
на |
плоскости |
|
и M0M взаимно |
||||||||
перпендикулярны, |
поэтому их скалярное произведение равно нулю: |
||||||||||
r |
uuuuur |
|
)+ B(y − y |
|
)+C (z − z |
|
)= 0 |
|
|||
n |
M |
0 |
M = 0 , т.е. A(x − x |
0 |
0 |
|
|||||
|
|
|
0 |
|
|
|
|
||||
Это уравнение называется уравнение плоскости в векторной форме. Вектор nr =(A, B,C ) называется нормальным вектором плоскости.
Обозначая через D = −Ax0 − By0 −Cz0 , запишем уравнение в виде
Ax + By +Cz + D = 0
Это уравнение называется общим уравнением плоскости. 57

Частные случаи общего уравнения плоскости:
1. Если D = 0 , то уравнение принимает вид Ax + By +Cz = 0 . Этому уравнению удовлетворяет точка O(0,0,0). Плоскость проходит
через начало координат.
2. Если C = 0 , то уравнение принимает вид Ax + By + D = 0 . Нормальный вектор nr =(A, B,0) перпендикулярен оси Oz .
Следовательно, плоскость параллельна оси Oz ; если B = 0 — параллельна оси Oy , если A = 0 — параллельна оси Ox .
3.Если C = D = 0, то плоскость проходит через O(0,0,0) параллельно оси Oz , т.е. проходит через ось Oz . Аналогично с другими осями.
4.Если A = B = 0, то уравнение принимает вид Cz + D = 0 или z = − CD .
Плоскость параллельна плоскости Oxy . Аналогично с другими
плоскостями.
5. Если A = B = D = 0 , то уравнение принимает вид Cz = 0 или z = 0 . Это уравнение плоскости Oxy . Аналогично с другими плоскостями.
Через три точки пространства, не лежащие на одной прямой, проходит единственная плоскость. Найдем уравнение плоскости Q ,
проходящей |
через точки |
M1 (x1, y1, z1 ), M2 (x2 , y2 , z2 ) |
и M3 (x3 , y3 , z3 ). |
|||
Возьмем произвольную точку |
M |
(x, y, z) на плоскости и составим векторы |
||||
uuuuur |
, y − y1z − z1 ), |
uuuuuur |
=(x2 |
− x1, y2 − y1, z2 − z1 ), |
|
|
M1M =(x − x1 |
M1M2 |
|
||||
uuuuuur |
|
|
|
|
|
|
M1M3 =(x3 − x1, y3 − y1, z3 − z1 ). |
Эти |
векторы лежат в |
плоскости Q , |
|||
следовательно, они компланарны. Запишем условие компланарности трех векторов (смешанное произведение равно нулю):
x − x1 x2 − x1 x3 − x1
y − y1 y2 − y1 y3 − y1
z − z1
z2 − z1 = 0 . Т.о. это уравнение плоскости проходящей z3 − z1
через три точки.
Пусть плоскость отсекает на осях Ox , Oy и Oz соответственно
отрезки a,b,c , |
т.е. проходит через точки |
A(a,0,0), B(0,b,0), C (0,0,c). |
|||||
Подставляя координаты точек в предыдущее уравнение, получим |
|
||||||
|
x −a |
y |
z |
|
|
|
|
|
|
|
|
||||
|
−a |
b |
0 |
|
= 0 . |
|
|
|
−a |
0 |
c |
|
|
|
|
Раскрыв |
определитель, получим |
bcx + acy + abz = abc |
или |
||||
ax + by + cz =1 уравнение плоскости в отрезках. 58
Положение плоскости Q полностью определяется единичным
вектором er, имеющим направление перпендикуляра опущенного на плоскость из начала координат, и длиной p этого перпендикуляра.
Пусть α, β,γ — углы, образованные |
e |
с осями координат. Тогда |
|||||
er =(cosα,cos β,cosγ ). |
Возьмем |
на плоскости |
произвольную |
точку |
|||
M (x, y, z) и ее радиус-вектор |
uuur |
(x, y, z). |
|
прerrr = p , т.е. |
|||
rr =OM = |
Тогда |
||||||
rr er = p нормальное |
уравнение |
плоскости |
в векторной |
форме. |
Зная |
||
координаты векторов можно записать xcosα + y cos β + z cosγ = p .
Это уравнение называется нормальным уравнением плоскости в координатной форме.
Отметим, что общее уравнение плоскости можно привести к нормальному уравнению умножив обе части уравнения на нормирующий
множитель λ |
= |
|
|
1 |
|
|
, где знак берется противоположным знаку |
|||||||||||||||||
± |
A2 + B2 +C2 |
|||||||||||||||||||||||
свободного члена D общего уравнения плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ПЛОСКОСТЬ. ОСНОВНЫЕ ЗАДАЧИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пусть заданы две плоскости Q1 и Q2 : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
A1x + B1 y +C1z + D1 = 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
A2 x + B2 y +C2 z + D2 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Угол |
|
ϕ |
между |
|
плоскостями |
это угол |
между |
|
|
нормалями |
|||||||||||||
nr |
=(A , B ,C ) |
и |
nr |
=(A , B ,C |
|
). |
Поэтому |
cosϕ = |
|
|
|
rnr1 |
|
|
|
nrr2 |
|
или |
||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||
1 |
1 |
1 |
1 |
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
n1 |
|
|
|
n2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cosϕ = |
|
|
A1 A2 + B1B2 +C1C2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A2 |
+ B2 +C2 |
A2 |
+ B2 |
+C2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
1 |
|
1 |
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если плоскости перпендикулярны, то перпендикулярны и их |
|||||||||||||||||||||||
нормали, т.е. |
A1 A2 + B1B2 +C1C2 = 0 |
|
— условие перпендикулярности двух |
|||||||||||||||||||||
плоскостей.
Если плоскости параллельны, то параллельны и их нормали, т.е.
A1 = B1 = C1 — условие параллельности двух плоскостей.
A2 B2 C2
Пусть задана точка M0 (x0 , y0 , z0 ) и плоскость Q своим уравнением Ax + By +Cz + D = 0 . Расстояние d от точки до плоскости находится по формуле
d = Ax0 + By0 +Cz0 + D . A2 + B2 +C2
59
УРАВНЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Положение прямой в пространстве определено, если задана какая- |
|||||||||||||||||||||||||||||||
либо точка M0 (x0 , y0 , z0 ) |
|
на прямой и вектор S =(m,n, p), параллельный |
||||||||||||||||||||||||||||||||
этой прямой — направляющий вектор. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Возьмем на прямой произвольную точку M (x, y, z). Обозначим |
|||||||||||||||||||||||||||||||
радиус-векторы точек M |
|
и |
M соответственно |
r |
и r . Очевидно, что |
|||||||||||||||||||||||||||||
r |
r |
|
|
uuuuur |
uuuuur |
|
0 |
r |
где |
t — |
|
|
|
|
|
|
|
0 |
|
|
|
называемый |
||||||||||||
r |
= r0 |
+ M0M , |
но M0M =tS , |
|
числовой множитель, |
|||||||||||||||||||||||||||||
параметром. Окончательно запишем rr = rr0 +tS . Это уравнение называется |
||||||||||||||||||||||||||||||||||
векторным уравнением прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Замечая, |
что |
rr =(x, y, z), |
r |
=(x , y , z |
0 |
), |
tS =(tm,tn,tp), |
векторное |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение прямой можно записать в виде |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
r |
|
r |
r |
|
|
|
|
r |
(y +tn) |
r |
+(z |
|
|
|
|
|
|
|
|
Отсюда |
|
|
следуют |
|||||||||||
xi + yj |
+ zk |
=(x +tm)i + |
j |
0 |
+tp)k . |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенства: |
x = x0 +tm, |
|
|
y = y0 +tn , |
|
z = z0 +tp . |
Они |
называются |
||||||||||||||||||||||||||
параметрическими уравнениями прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
uuuuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Векторы M |
0M |
и |
S |
коллинеарные, |
значит |
их |
координаты |
||||||||||||||||||||||||
пропорциональны: |
|
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
Это |
|
|
уравнение |
называют |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
n |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каноническим уравнением прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
Замечание. Обращение в ноль одного из знаменателей означает |
|||||||||||||||||||||||||||||||
обращение в ноль соответствующего числителя. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Пусть прямая проходит через точки M1 (x1, y1, z1 ), M2 (x2 , y2 , z2 ). В |
|||||||||||||||||||||||||||||||
качестве |
направляющего |
|
вектора |
|
|
|
можно |
взять |
|
вектор |
||||||||||||||||||||||||
r |
uuuuuur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m = x2 − x1 , |
|
n = y2 − y1 , |
|||||||||
S |
= M1M2 =(x2 − x1, y2 − y1, z2 − z1 ), |
следовательно |
|
|
||||||||||||||||||||||||||||||
p = z |
2 |
− z . |
Согласно уравнению, |
можно записать |
|
x − x1 |
= |
y − y1 |
= |
z − z1 |
, |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − x1 |
|
y2 − y1 |
|
z − z1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
уравнение прямой, проходящей через две точки.
Прямую в пространстве можно задать как линию пересечения двух
непараллельных плоскостей: A1x + B1 y +C1z + D1 = 0
A2 x + B2 y +C2 z + D2 = 0
Это общее уравнение прямой. От него можно перейти к каноническому уравнению. Координаты точки M0 получаем из системы
уравнений, придав одной переменной произвольное значение (например,
60
