Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lineynaya algebra i analitich_geom / Kuznecova_s_n_lukin_m_v_lineynaya_algebra_i_analiticheskaya

.pdf

Скачиваний:

Добавлен:

06.06.2015

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Свойстваr r r rскалярного произведения

1.a b =b a ;

2.(λar) br = λ(ar br); ar (br +cr)= ar br + ar cr;

r	2	r	2	или	r	r	2	;
3. a		= a		или	a =	a		;

r r r r

4.a b a b = 0 ;

5.Выражение скалярного произведения через координаты

Найдем скалярное произведение векторов, перемножая их как

многочлены

br =(axri + ay rj + az kr) (bxri +by rj +bz kr)=

= axbxi ii

+ axbyij

+ axbzik +

rrr

aybx jii

+ ayby jj

+ aybz jk +

azbxki + azbykj + azbz kk =

принимая во внимание, что

= axbx

r r

+0 +0 +0 + ayby +0 +0 +0 + azbz .

Окончательно

получим:

a b = axbx + ayby + azbz

6. Угол между векторами cosϕ =

;

a b

7. Проекция вектора на заданное направление прr a

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

Три некомпланарных (не лежащих в одной плоскости) вектора a , b

и c , взятые в указанном порядке, образуют правую тройку, если с конца

вектора

кратчайший поворот от вектора a к вектору br

виден

совершающимся против часовой стрелки, и левую, если по часовой.

Векторным произведением вектора a на вектор b

называется вектор

×b , который:

r r

•

перпендикулярен векторам a и b , т.е. a ×b a,

a ×b

b ;

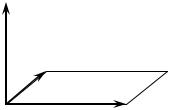
• имеет длину, численно равную площади параллелограмма,

построенного

на

векторах a и b как на сторонах, т.е.

ar×br

sinϕ ;

•

векторы a , b

a ×b образуют правую тройку.

•

Обозначается

r r

×b

a,b

r r

a ×b

				a
Из		определения		вытекают	следующие	соотношения
ir× rj = kr, rj ×kr = ir, kr×ir				= rj
Свойства векторного произведения
1. ar×br		= −(br	×ar);
2. λ(ar×br)=(λar)×br = ar×(λbr);
3. (ar +br)×cr = ar×cr +br×cr;
r	r	r	r
r	r	r	r
4. a	b a ×b = 0 ;
5. Выражение векторного произведения через координаты
Найдем векторное произведение векторов
ar×br		=(axir	+ ay rj + az kr)×(bxir +by rj +bzkr)=

= axbx (ir×ir)+ axby (ir× rj )+ axbz (ir×kr)+ aybx (rj ×ir)+ ayby (rj × rj )+ aybz (rj ×kr)+ azbx (kr×ir)+ azby (kr× rj )+ azbz (kr×kr)=

принимая во внимание, что

	i	j	k
i	0	k	− j
j	−k	0	i
k	j	−i	0

= 0r + axbykr −axbz rj −aybxkr +0r + aybzir + azbx rj −azbyir +0r =

=(aybz −azby )ir −(axbz −azbx )rj +(axby −aybx )kr =

−

rj +

ar×br =

ir −

rj +

kr или ar×br

Sпар

, S =

×b

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ И ЕГО СВОЙСТВА

Рассмотрим

произведение векторов a , b

cr,

составленное

следующим

образом:

( ar×b ) cr. Такое

произведение

называется

векторно-скалярным или смешанным.

( ar×br) cr.

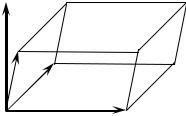
Выясним геометрический смысл выражения

Построим

и вектор

параллелепипед, ребрами которого являются векторы a , b

d =

×b .

rrr

abc

Имеем :(ar×b ) cr = dr cr =

прdurcr,

ar×br

= S , где S

— площадь

параллелограмма, построенного на векторах a и b

, прrc = H для правой

тройки

векторов

прrcr

= −H

—

высота

для

левой,

где

(ar×b ) cr = S (±H )= ±V ,

параллелепипеда. Получаем:

где

—

объем

параллелепипеда, образованного векторами a ,

b и c .

Т.о., смешанное произведение трех векторов равно объему

параллелепипеда,

построенного на

этих векторах, взятому

со

знаком

«плюс», если эти векторы образуют правую тройку, и со знаком «минус", если они образуют левую тройку.

Свойства смешанного произведения
1. (ar×br) cr =(br×cr) ar =(cr×ar) br;
2. (ar×br) cr = ar (br×cr);
rrr	rrr	rrr	rrr rrr	rrr
3. abc	= −acb,	abc	= −bac, abc	= −cba ;

4.(ar×br) cr = 0 ar, br и c — компланарны;

5.Выражение смешанного произведения через координаты

(ar×br) cr =((axir + ay rj + az kr)×(bx i +by rj +bz kr)) cr =

(cxi +cy j

+cz k )=

cx −

cz ;

rrr

abc

rrr

> 0, то a , b

6. Взаимная ориентация векторов в пространстве: если abc

r r

< 0 , то

a , b и c — левая тройка;

и c — правая тройка, если abc

7. Vпар =

rrr

, Vпир =

rrr

abc

ТЕМА IV. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

n-МЕРНЫЙ ВЕКТОР

Ранее было сказано, что матрица, содержащая один столбец или одну строку, называется вектором. Теперь мы дадим более строгое определение этого понятия.

Последовательность n действительных чисел называется n -мерным вектором. Обозначается ar =(a1,a2 ,K,an ).

Числа a1,a2 ,K,an называются координатами						вектора,	а	n –
размерностью вектора.						br =(b ,b ,K,b
Два	n -мерных вектора ar =(a ,a ,K,a			n	) и	br =(b ,b ,K,b			)
			1 2	n		1	2	n
называются равными, когда равны их соответствующие координаты:
	a1 =b1
r r	a	=b
	2	2	.
a =b		K	.
		K
	a	=b
	n	n
			34

ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД n-МЕРНЫМИ ВЕКТОРАМИ

Суммой векторов

ar =(a ,a ,K,a

) и b =(b ,b ,K,b )

называется

=(a +b ,a +b ,K,a

вектор a +b

Произведением вектора

a =(a1,a2 ,K,an ) на число

называется

вектор λar =(λa ,λa ,K,λa

Вектор 0

называется нулевым, если для любого вектора выполняется

равенство

= a .

вектору ar,

Вектор

−ar

называется

противоположным

если

+(−a)=

Т.к. операции

над

n -мерными

векторами определяются

через

операции над их координатами, то многие свойства арифметических

операцийrсправедливыr и для операций над векторами:

1. ar +b =b + ar;

2. (ar +br)+cr = ar +(br +cr);

3. λ1 (λ2ar)=(λ1λ2 )ar;

4. (λ1 +λ2 )ar = λ1ar +λ2ar;

5. λ(ar +br)= λar +λbr;

6. 1 ar = ar.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ. ДЛИНА

Скалярным

произведением

векторов

a =(a1,a2 ,K,an )

=(b ,b ,K,b ) называется число:

1 r

2 r

b =(a b + a b +K+ a b

1 1 2

n n

a =(a1,a2 ,K,an )

Длиной

(модулем)

вектора

называется

число

= ar2 .

a =(a ,a ,K,a

)

и br =(b ,b ,K,b

)

Углом

между

векторами

1 2

называется число ϕ [0,π], для которого cosϕ =

ar b

n-МЕРНОЕ ВЕКТОРНОЕ ПРОСТРАНСТВО. БАЗИС

Множество L элементов x, y,K,z называется линейным (векторным)

пространством, если:

1. Для любых двух элементов x L и y L определена операция сложения;

2.Для любого элемента x L и любого числа α определена операция умножения элемента x на число α ;

3.Определено равенство элементов из L ;

4.Операции (1) и (2) удовлетворяют условиям:

a.x+ y = y+ x ;

b.(x+ y)+ z = x+(y+ z);

c.α(β x)=(αβ)x ;

d.(α + β)x =α x+ β x ;

e.α(x+ y)=α x+α y ;

f.существует элемент, называемый нулевым, такой, что x+0 = x ;

g.для любого x L имеет место x 1 =1 x = x

h.для любого x L существует элемент −x , называемый противоположным, такой, что x+(−x)= 0 .

Совокупность всех n -мерных векторов образует линейное векторное

пространство Rn .

Свойства линейного векторного пространства:

1. В каждом линейном векторном пространстве существует единственный элемент 0;

2.В каждом линейном векторном пространстве любому элементу соответствует единственный противоположный элементr ;

3.Для всякого элемента ar справедливо равенство 0 arr= 0 ;

4.Для любого числа α справедливо равенство α 0 = 0 ;

5.Для каждого элемента a справедливо −a =(−1) ar.

Пример. Убедимся в том, что множество всех диагональных матриц порядка n образуют линейное пространство.

Решение. Для матриц определена операция сложения и умножения на число. Свойства действий следуют из свойства действий над

						0	0	K 0
						0	0	K 0
матрицами. Нулевой элемент O =						0	0	K 0	, противоположенный
					K K K K
						0	0	K 0
						0	0	K 0
−a11		0	K	0
	0	−a22	K	0	.
элемент O =	K	K	K		.
	K	K	K	K
	0	0
	0	0	K −ann

ЛИНЕЙНАЯ НЕЗАВИСИМОСТЬ ВЕКТОРОВ

Определяется также как в случае трехмерных геометрических

векторов: если для системы k векторов a1,ar2 ,K,ark равенство ∑k λiari = 0r

i=1

верно только при λi = 0 (i =1,K,k ), то эта система называется линейно

независимой.

Следовательно, решение вопроса о линейной зависимости или независимости системы из k n -мерных векторов сводится к исследованию линейной однородной системы n уравнений с k неизвестными:

a λ + a λ +K+ a λ = 0
	11 1	12	2	1k	k
a21λ1 + a22λ2				+K+ a2k	λk = 0	.
						.
KKKKKKKKKKKK
a	λ	+ a	λ	+K+ a	λ = 0
	n1 1	n2	2	nk	k

Можно показать, что если векторы a1,ar2 ,K,ark линейно зависимы, то

хотя бы один из них можно представить в виде линейной комбинации остальных и наоборот.

БАЗИС ЛИНЕЙНОГО ВЕКТОРНОГО ПРОСТРАНСТВА И КООРДИНАТЫ ВЕКТОРА

er	,er	Любая совокупность n линейно		независимых векторов
er	,er	,K,er	называется базисом пространства Rn ,	если каждый вектор из
1	2	n

пространства Rn можно представить в виде линейной комбинации векторов этой совокупности, т.е. x = x1er1 + x2er2 +K+ xnern .

Такое представление вектора называется разложением его по данному базису. Числа x1, x2 ,K, xn называются координатами вектора в

этом базисе.

Теорема IV.1 Координаты вектора относительно некоторого базиса er1,er2 ,K,ern определяются единственным образом.

	Доказательство:
	Пусть имеется два разложения некоторого вектора xr							относительно
базиса er1,er2 ,K,ern :
xr	= x1er1 + x2er2 +K+ xnern
r	′r	′r		′r
x	= x1e1 + x2e2		+K+ xnen
0r	Вычитая из первого равенства второе, получим:
0r	=(x	− x′)er	+(x	− x′)er +K+	(x	− x′ )er .
	1	1 1	2	2 2	n	n	n
	Т.к. векторы er1,er2 ,K,ern линейно независимы, то значит, что
коэффициенты линейной комбинации							могут быть только	нулями, т.е.
x1 = x1′, x2 = x2′,K, xn = xn′ .
						37

Одним из базисов пространства Rn является система
er	=(1,0,K,0)
1	=(0,1,K,0)
er	=(0,1,K,0)
2
er		K
er	=(0,0,K,1)
n
Действительно, система
1 0 K 0		λ			0
0 1 K	0		λ1			0	тривиальное	(нулевое)
			2 =			имеет только	тривиальное	(нулевое)
K K K K		K			K
			λn
0 0 K	1		λn			0
решение. Значит система векторов e1,er2 ,K,ern линейно независима. И
любой вектор ar =(a ,a ,K,a				n	)	разлагается по этой системе		er	,er	,K,er
	1	2		n				1	2	n
следующим образом ar		= a1er1 + a2er2 +K+ anern . Т.е.					координаты вектора это
коэффициенты в разложении этого вектора по базису e1,er2 ,K,ern .

Любой другой базис пространства Rn также состоит из n векторов.

Размерностью пространства Rn называется число векторов в любом его базисе. Это означает, что если размерность пространства равна n , то в нем можно указать n линейно независимых векторов, а любые n +1 векторов этого пространства линейно зависимы.

ПЕРЕХОД К НОВОМУ БАЗИСУ

Поскольку Rn может иметь не единственный базис встает вопрос, о переходе от разложения в одном базисе к разложению в другомr r базисе.

Пусть имеется два базиса: e1,er2 ,K,ern и ε1,ε2 ,K,εn , и пусть

некоторый вектор раскладывается по

Очевидно, что векторы базиса ε1,εr2 ,K,εrn базису er1,er2 ,K,ern :

εr1	=τ11er1			+τ21er2		+K+τn1ern
r			r		r			r
ε2	=τ12e1			+τ	22e2	+K+τn2en .
		KKKKKK
r	=τ		r	+τ	r	+K+τ		r
ε	=τ	1n	e	+τ	e	+K+τ	nn	e
n		1n	1		2n 2		nn	n

базисам	r	n	r	n	′r
базисам	x	= ∑xiei		= ∑xiεi .
		i=1		i=1

также можно разложить по

Составим матрицу перехода T :

x′

K τ

τ22

K τ

′

T =

τ21

X =

, X ′ =

, тогда X =T X ′ или обратное

K K K K

τn2

′

τn1

K τnn

соотношение X ′=T −1 X .

Матрица

T называется матрицей преобразования координат при

переходе от базиса er1,er2 ,K,ern

к базису ε1,εr2 ,K,εrn .

базисе er1,er2 ,er3 .

Пример.

Координаты

вектора x =(6;6;1)

даны

Записать

его

координаты

базисе

= e +er

er ,

εr = −5er

−er ,

εr3 = −er1 +er2 +er3 .

−5

−1

Решение.

Запишем

матрицу перехода

−1

. Строим

T =

1 −5 −1

1 −5 6

обратную

матрицу

= −1 ≠ 0 .

Поэтому

−1

−116

2 .

−6

−4

1 −5 6

−3

Тогда x′ =

−116

−8

−4

−

ЕВКЛИДОВО ПРОСТРАНСТВО

Линейное пространство называется евклидовым, если в нем определена операция, ставящая в соответствие любым двум элементам x L и y L число, называемое скалярным произведением и

обозначаемое (x, y), для которого выполняется:

1.(x, y)=(y,x);

2.(x+ y,z)=(x,z)+(y,z);

3.(α x, y)=α(x, y);

4.(x,x)≥ 0, причем (x,x)= 0 x = 0 .

Обозначается En .

Линейное пространство называется нормированным, если каждому элементу x L поставлено в соответствие неотрицательное число, называемое его нормой x . При этом выполняются аксиомы: