4.4. Примеры расчёта газовых течений с помощью уравнений расхода и количества движения

Важное место в инженерных приложениях газовой динамики занимает расчёт сопел, дозвуковых и сверхзвуковых (сопла Лаваля), диффузоров и течений в трубах. Прежде чем перейти к примерам расчёта, сделаем краткие пояснения к вышеизложенному материалу.

Ускорение газового потока в сужающемся сопле, в соответствии с уравнением обращения воздействий, возможно только до скорости звука. Расход через сопло определяется давлением и температурой торможения, а также геометрией сопла. При достижении критического режима течения число Маха M и коэффициент скорости λ равны единице и перестают увеличиваться. Если давление на входе в сопло повышается, то соответственно растёт давление на срезе сопла без увеличения скорости истечения. Таким образом, всегда выполняется критическое отношение давлений:

= (4.17)

Для воздуха (k = 1,4) это отношение равно 0,5283

Таким образом, если 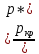, то весь перепад давлений не может быть использован для дальнейшего разгона поток в сужающемся сопле, оно как бы "запирается" (B₀ – атмосферное давление). Для того чтобы увеличить скорость потока, уже в сверхзвуковой области, в соответствии с уравнением обращения воздействий к сужающемуся соплу должен быть присоединён расширяющийся канал. Другим словами, достижение сверхзвуковой скорости возможно только в сопле Лаваля, при этом давление на срезе сопла может быть и больше, и меньше атмосферного (при истечении в атмосферу). Только на расчётном режиме давление на срезе сопла равно атмосферному давлению (p_a = B₀).

Если общий перепад давлений в сопле Лаваля , то ускорения потока не будет, газ в расширяющейся части сопла начнёт тормозиться, и сопло Лаваля превратится в трубу Вентури. Поскольку расход через геометрическое сопло есть величина при данных условиях постоянная, то баланс расходов через критическое и выходное сечения сопла без учёта потерь полного давления имеет следующий вид:

m = m ,откуда следует важная формула:

q(λ_a) = (4.18)

Теперь рассмотрим несколько задач на расчёт течениё в соплах и диффузорах.

Задача

Подобрать площадь выходного сечения сверхзвукового сопла Лаваля, обеспечивающего расход воздуха 1 кг/с при расчётном течении. Давление на входе в сопло 0,5 МПа, температура торможения потока 15

Решение

Дано:

G_в = 1кг/с

p*= 0,5 МПа

T*= 288 K

B₀ = 0,1 МПа

F_a = ?

Расчётным называется истечение, при котором на срезе сопла устанавливается давление окружающей среды. В качестве допущения рассматриваем течение без потерь полного давления.

Площадь критического сечения:

F_кр= == 0,00112 м² (11,2 см²)

= 0,2

Определяем площадь выходного сечения сопла Лаваля:

= q(λ)

Задача

Для условий первой задачи определить площадь выходного сечения сужающегося сопла и статическое давление на срезе сопла.

Поскольку в выходном сечении сужающегося сопла при сверхкритическом перепаде давлений скорость потока равна скорости звука, то газодинамическая функция q(λ) = 1. Соответственно имеем:

F_кр= ==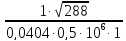 0,00084 м^{2 2}

Статическое давление на срезе сопла равно:

p*