4.2. Газодинамическая форма уравнения расхода

В уравнении массового секундного расхода G = ρwF выразим значения ρ и w через параметры торможения p* и T* и коэффициент скорости λ:

G = (4.9)

Далее ρ = ρ*=

w = λ

Введём газодинамическую функцию q(λ), которая имеет физический смысл безразмерной плотности тока:

q(λ) =

Функция q(λ) может быть представлена следующим образом:

q(λ) = ·(4.10)

Правую часть выражения (4.10) умножим и разделим на в (4.9) и после несложных преобразований получим:

G = или

G = m (4.11)

где коэффициент m =

Для воздуха (k = 1,4; R = 287,4 )m = 0,0404. Для продуктов сгорания ГТД (k = 1,33; R = 288,4 )m = 0,0396

Введём в формулу (4.11) статическое давление p = p* В результате получаем следующее выражение для газодинамического уравнения расхода:

G = m (4.12)

где y(λ) = - вторая газодинамическая функция потока массы.

На рис.4.2 приведены зависимости газодинамических функций q (λ) и y(λ) от коэффициента скорости λ.

Рис.4.2.Зависимости газодинамических функций q (λ) и y(λ) от коэффициента скорости λ

При увеличении λ от 0 до 1 значение газодинамической функции q (λ) растёт до единицы при λ = 1, после чего уменьшается до нуля. Одно им то же значение q (λ) соответствует двум возможным значениям коэффициента скорости λ (λ и λ). Таким образом, плотность тока максимальна при значении q (λ) = 1. Как видно на графике рис.4.1 значение газодинамической функции y(λ) с увеличением λ монотонно возрастает.

Уравнения расхода в газодинамической форме удобны для расчётов течений в различных задачах, включая течения газа в соплах и диффузорах.

4.3. Уравнения количества движения в полных импульсах

Полным импульсом называется сумма силы от секундного количества движения и силы давления:

Ф = Gw + pF (4.13)

Выразим полный импульс в функции коэффициента скорости λ.

Ф = G (w + ) = G[λ]

w = λ = RT = RT*(1 –

После раскрытия скобок и несложных преобразований получаем следующее выражение для полного импульса:

Gw + pF = Ga_кр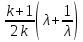= Ga_кр z(λ) (4.14)

Выражение (4.14) известно как преобразование Б.М.Киселёва.

В (4.14) введена газодинамическая функция потока импульса z(λ) = λ + .

С использованием уравнений расхода (4.11) и (4.12) в (4.14) можно ввести газодинамические функции q(λ) и y(λ) и выразить полный импульс через две другие газодинамические функции потока импульса f(λ) и r(λ). В результате получаем следующие выражения:

Gw + pF = p*F·f(λ) (4.15)

Gw + pF = pF· (4.16)

Газодинамические функции f(λ) и r(λ) описываются следующими формулами:

f(λ) = r(λ) =

Полный импульс в потоке сохраняет постоянное значение, если равнодействующая всех сил, спроектированная на направление движения, равна нулю.

Полученные выражения удобны для вычисления газовых сил, действующих на стенки канала, в частности, для определения тяги реактивного двигателя. На рис.4.3 приведены зависимости газодинамических функций потока импульса от коэффициента скорости λ. Они сведены также в таблицы газодинамических функций.

Рис.4.3. Графики зависимостей газодинамических функций потока импульса от от коэффициента скорости λ