3.6. Примеры расчётов параметров движущегося газа

Измерение полного и статического давления в газовом потоке

Для измерения статического давления в потоке жидкости, движущейся в канале, в стенке последнего в нужном сечении перпендикулярно к оси канала делается небольшое отверстие диаметром 0,8 – 1,0 мм, которое соединяется трубкой с манометром. Для измерения полного давления (давления торможения) применяется Г-образная трубка, в которой поток тормозится практически до нуля. Отборник полного давления, который называется «трубка Пито», также соединяется с манометром. Схема измерений полного и статического давления, а также температуры потока, показана на рис. 3.7.

Рис. 3.7. Схема измерений полного и статического давления в канале

Параметры торможения являются параметрами состояния заторможенного потока и связаны между собой уравнением состояния:

p^* = ρ^*R*T*

Сопоставляя это уравнение с обычным уравнением состояния в статических параметрах, получим следующую связь между газодинамическими функциями параметров торможения:

Поскольку = , измерения по схеме рис. 3.6 могут быть использованы для определения скоростей в точках замера при дозвуковом течении газа. Поскольку в расчётах используется плотность потока, схема измерения должна быть дополнены датчиком температуры.

Задача 3.1

При каком показании () ртутногоU – образного манометра, подсоединённого к трубке Пито, свободный поток воздуха движется при числе Маха 0,5? Атмосферное давление равно B₀ = 760 мм рт. ст.

Решение

В свободном потоке воздуха атмосферное давление равно давлению торможения потока (p*= B₀). По таблицам газодинамических функций (ГДФ) для показателя адиабаты k = 1,4 (воздух) и числа Маха M = 0,5 находим газодинамическую функцию

= 0,843 p = 640,7 мм рт.ст., откуда

Эта задача может быть решена без использования таблиц газодинамических функций по формуле (3.36):

p = = 640,7 мм рт.ст.

Задача 3.2

Определить полное давление и температуру торможения в критической точке ракеты, летящей на высоте 20000 метров (p = 41 мм рт. ст., t = - 56,5

Решение

Число Маха M = ; (где a – скорость звука)

p* = p·

a = 20,1= 296 м/с

M = = 3,28

p* = 41·133,3·303746,59 Па

T* = T·(1 + 3,28²) = 216,5·(1 + 10,7584) = 2445,69

Глава 4. Одномерное движение газа

4.1. Уравнение обращения воздействий

Исходными уравнениями для вывода уравнения обращения воздействий являются уравнение неразрывности, уравнение состояния и уравнение Бернулли для элементарной струйки. Логарифмируя и дифференцируя уравнение неразрывности G = ρwF, получаем:

= + (4.1)

Дифференцируя уравнение состояния p = ρRT, после деления на ρ получаем:

= R(dT + T) (4.2)

Уравнение Бернулли в дифференциальной форме имеет вид:

= - wdw – dL_тех - dL_тр (4.3)

Из (4.1) и (4.2) получаем:

= RdT + RT()(4.4)

Сопоставление (4.4) с (4.3) после введения выражения для скорости звука a² = kRT даёт следующее уравнение:

RdT + () + (w² - )+dL_тех + dL_тр = 0 (4.5)

поскольку wdw - =(w² - )

От члена RdT избавимся с помощью дифференциального уравнения энергии:

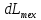dQ_н = di + d=RT + wdw + (4.6)

(так как di =c_pdT = dT )

Подставляем (4.6) в (4.5) и после несложных преобразований получаем уравнение обращения воздействий, связывающее изменение скорости потока с внешними воздействиями – геометрическим, расходным, механическим, тепловым и воздействием трения:

(M² - 1) =-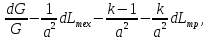(4.7)

где в правой части уравнения указанные выше воздействия по порядку.

Уравнение обращения воздействий было выведено Л.А.Вулисом и может рассматриваться как условие обращения воздействий, поскольку устанавливает условия, при которых возможен переход через скорость звука, то есть через критическое значение скорости. Из уравнения обращения воздействий следует очень важный вывод: односторонним воздействием нельзя перевести скорость дозвукового потока через критическое значение, то есть в сверхзвуковую область – для этого нужно сменить знак воздействия.

Наиболее часто в технике мы встречаемся с геометрическим воздействием, которое имеет место в сопле Лаваля, представляющее собой внач але сужающийся, а затем, после критического сечения, расширяющийся канал. Если прочие воздействия отсутствуют, то уравнение для геометрического воздействия принимает вид:

= (4.8)

Уравнение (4.8) носит также название уравнение Гюгонио, которое было выведено независимо от уравнения (4.7) из уравнений неразрывности и Бернулли. Анализируя это уравнение, видим, что для ускорения дозвукового потока сопло должно сужающимся, так как при M dF

Для получения сверхзвукового потока после достижения скорости звука в критическом сечении сопло должно быть расширяющимся, тка как при M dF

Скорость потока и безразмерная площадь проходного сечения сопла Лаваля связаны однозначным соотношением, которое графически представлено на рис. 4.1.

Рис.4.1. Зависимость безразмерной площади сопла Лаваля от числа M

Давление, температура и плотность газа в идеальном термодинамическом процессе связаны уравнением состояния и, таким образом, в произвольном сечении сопла Лаваля имеется определённое значения числа Маха, которое зависит от полного давления в камере перед соплом. Соответственно, так как статическое давление в сечениях сопла определяется числом Маха, то давление на срезе сверхзвукового сопла зависит только от давления в камере перед соплом и от формы сопла. Расчёт течений в соплах и диффузорах представлен ниже в этой главе.

В каждом воздействий из других воздействий для перехода через критическую скорость (M = 1) нужно изменить знак воздействия. Например, в расходном сопле для ускорения потока на дозвуковом участке нужно подводить дополнительную массу жидкости, а на сверхзвуковом участке отводить её. В тепловом сопле подводом тепла к движущемуся газу можно увеличить его скорость только до критического значения, а для перехода через скорость звука нужно отводить тепло. Аналогично обстоит дело с механическим соплом. В дозвуковой области нужно подводить работу (компрессор), а в сверхзвуковой – отводить (турбина). Только трение является односторонним воздействием, поскольку оно всегда существует и его нельзя отвести. Работа сил трения всегда положительна, и переход через скорость звука воздействие трения невозможен.