
- •Московский государственный машиностроительный университет (мами)
- •Газовая динамика
- •Москва - 2015
- •Глава 1. Основные понятия газовой динамики и физические свойства жидкостей и газов …………………………………………………….
- •Глава 3. Уравнения газовой динамики элементарной струйки
- •3.1. Уравнение неразрывности
- •3.2. Уравнение количества движения (первое уравнение Эйлера)
- •3.3. Уравнение моментов количества движения (второе уравнение Эйлера)
- •3.4. Уравнение энергии
- •Механическая форма уравнения энергии
- •3.5. Параметры торможения
- •3.6. Примеры расчётов параметров движущегося газа
- •Глава 4. Одномерное движение газа
- •4.1. Уравнение обращения воздействий
- •4.2. Газодинамическая форма уравнения расхода
- •4.3. Уравнения количества движения в полных импульсах
- •4.4. Примеры расчёта газовых течений с помощью уравнений расхода и количества движения
- •Глава 5. Скачки уплотнения и ускорение газового потока
- •5.1. Плоская ударная волна и прямой скачок уплотнения
- •5.2. Основное кинематическое и основное динамическое соотношения для прямого скачка уплотнения
- •5.3. Косые скачки уплотнения
- •5.4. Обтекание внешнего тупого угла сверхзвуковым потоком (течение Прандтля - Майера)
3.5. Параметры торможения
В соответствии с соотношением (3.21) температура газа становится равной температуре торможения тогда, когда скорость течения потока становится равной нулю при отсутствии обмена с окружающей средой. Поскольку i = cpT , температуру торможения выразим как (3.28):
T*
= T
+
 (3.28)
(3.28)
Теплоёмкость
воздуха равна 1005 Дж/кг град,
откуда для воздуха
град,
откуда для воздуха
T*
= T
+
 .
.
Температура термометра, помещённого в поток, приблизительно равна температуре торможения. Это объясняется образованием у стенок термометра пограничного слоя, в котором набегающий поток полностью затормаживается. Неподвижный термометр не может измерить статическую температуру в потоке газа, для этого пришлось бы перемещать его со скоростью потока. Поскольку температура торможения пропорциональна квадрату скорости, то поверхность тел, движущихся с очень высокой скоростью, сильно разогрета. Например, температура поверхности снаряда при скорости 1500 м/с превышает 1000 K. Температура обшивки турбореактивного самолёта, летящего со скоростью 800 км/ч (222,22 м/с) выше температуры за бортом примерно на 25◦C. Из-за очень высокого нагрева обшивки на спускаемых аппаратах космонавтов устанавливают специальные защитные экраны в виде огнеупорных пластин, которые частично сгорают в плотных слоях атмосферы. В реальных условиях величина динамической добавки температуры оказывается меньше вследствие теплообмена между полностью заторможенным и близлежащими слоями. В этом случае для расчёта вводится коэффициент восстановления температуры, который обычно определяется экспериментально и зависит от условий течения воздуха. Тогда
T*
= T
+ r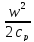 (3.29)
(3.29)
где r – коэффициент восстановления температуры. Например, указанных выше условий полёта самолёта r ≈ 0,8.
Из уравнения Бернулли (3.25) для несжимаемой жидкости и z = 0 следует:
p*
= p
+
 (3.30)
(3.30)
Давление p* называется давлением торможения, или полным давлением. Физический смысл уравнения (3.30) – это давление полностью заторможенного потока, когда скорость равна нулю. Уравнение (3.30) можно использовать в расчётах только при низких дозвуковых скоростях потока, когда сжимаемостью жидкости можно пренебречь, и ошибка расчётов в этих случаях будет незначительной.
В энергетически изолированном течении максимальная скорость может быть получена тогда, когда полная энтальпия будет превращена в кинетическую энергию, то есть при расширении газа до абсолютного вакуума (i = 0, p = o). Тогда в соответствии с (3.21) имеем:
Wmax
=
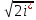 =
= (3.31)
(3.31)
Для воздуха (cp = 1005 Дж/кг∙град) формула (3.31) принимает следующий вид:
Wmax
= 44,833
 (3.32)
(3.32)
Разделим обе части (3.28) на T:
 =
=
 ,(3.33)
,(3.33)
где
a
–
скорость звука. При выводе последнего
выражения были использованы уравнение
Майера (cp
– cv
= R)
и отношение теплоёмкостей при постоянном
давлении и постоянном объёме ( = k).
Отношение скорости потока к скорости
звука в данной среде называется числом
Маха.
Число Маха является критерием подобия
газовых течений. Если число Маха меньше
единицы, то течение является дозвуковым,
если больше единицы – сверхзвуковым,
если число Маха равно единице, то течение
потока считается звуковым, или критическим.
Используя выражение числа Маха, можем
получить расчётную формулу для отношения
температуры торможения к статической
температуре в функции числа Маха:
= k).
Отношение скорости потока к скорости
звука в данной среде называется числом
Маха.
Число Маха является критерием подобия
газовых течений. Если число Маха меньше
единицы, то течение является дозвуковым,
если больше единицы – сверхзвуковым,
если число Маха равно единице, то течение
потока считается звуковым, или критическим.
Используя выражение числа Маха, можем
получить расчётную формулу для отношения
температуры торможения к статической
температуре в функции числа Маха:
 =
1 +
=
1 +
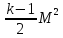 (3.34)
(3.34)
Вернёмся к уравнению Бернулли в виде (3.27)
 –1]
+
–1]
+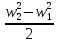 = 0
= 0
В случае идеального торможения потока жидкости, когда w2 = 0 и p2 = p*, получим (опуская индексы «1»):
 -
1] +
-
1] + = 0,
откуда
= 0,
откуда
 (3.35)
(3.35)
Используя
далее формулу скорости звука a
=
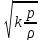 ,получим
выражение для отношения давления
торможения к статическому
давлению
в функции числа M:
,получим
выражение для отношения давления
торможения к статическому
давлению
в функции числа M:
 (3.36)
(3.36)
Выражение (3.35) можно получить, используя соотношения идеальной адиабаты:
 и
и
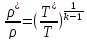
Из этих же соотношений можно получить формулу для расчёта плотности идеально заторможенного потока:

 (3.37)
(3.37)
Если скорость потока равна скорости звука, когда число Маха равно единице (M = 1), режим течения называется критическим. В этом случае из (3.33) получаем:
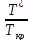 =
=
 (3.38)
(3.38)
Скорость звука для критического режима:
 =
=
 =
=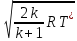 (3.39)
(3.39)
Для
воздуха (k
= 1,4)
aкр
=
18,3
Представим выражение (3.33) в следующем виде:



Откуда, используя (3.38), получаем следующее выражение:
 =
1
–
=
1
–
 (3.40)
(3.40)
где λ называется коэффициентом скорости и выражает отношение скорости потока к критической скорости звука:
λ
=
 (3.41)
(3.41)
Между λ и M имеется конкретная связь, которую представляют следующие соотношения:
λ2
=
 ;M2
=
;M2
=

При критическом режиме (λ = M = 1) максимальной скорости течения, когда T = 0, соответствует максимальное значение коэффициента скорости:
 =
=
 (3.42)
(3.42)
Для воздуха (k = 1,4) λmax = 2,45
Коэффициент скорости, также как и число Маха, может считаться критерием подобия газовых течений. Между ними имеется однозначная зависимость, которая легко может быть получена с использованием соотношений (3.34) и (3.40).
Из
уравнения (3.40) с использованием соотношений
идеальной адиабаты могут быть получены
уравнения для отношений
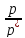 и
и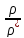 .
.
Таким образом, имеем следующие соотношения:
 =
1
–
=
1
–
 =
=
 =
=
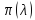
 =
ε
=
ε

Величины
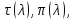 ε
ε
 называются
газодинамическими
функциями параметров торможения.
Эти очень важные величины применяются
в инженерных расчётах. Они сведены в
таблицы газодинамических функций,
составленных для различных значений
чисел M
и λ,
а также для различных показателей
адиабаты k.
называются
газодинамическими
функциями параметров торможения.
Эти очень важные величины применяются
в инженерных расчётах. Они сведены в
таблицы газодинамических функций,
составленных для различных значений
чисел M
и λ,
а также для различных показателей
адиабаты k.
Протекание кривых газодинамических функций параметров торможения показан на рис. 3.6.

Рис. 3.6. Газодинамические функции параметров торможения
