3.4. Уравнение энергии

Согласно первому закону термодинамики, который выражает закон сохранения энергии, тепло, подведённое к элементу жидкости (газа), идёт на совершение технической работы, работы сил трения и на изменение его внутренней, потенциальной и кинетической энергии. В дифференциальной форме уравнение энергии для единицы массы газа имеет следующий вид:

dq = dq_н + dq_тр = dL_тех + dL_тр + dU + gdz dd, (3.13)

где q_н – внешнее (наружное) тепло, подведённое к газу, q_тр - внутреннее тепло, подведённое к газу при действии сил трения; L_тех– техническая работа (компрессор, турбина и др.), L_тр – работа сил трения, U – внутренняя энергия единицы массы газа, gz – потенциальная энергия уровня, - потенциальная энергия давления единицы массы газа, - кинетическая энергия единицы массы газа.

Все указанные величины измеряются в .

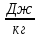После интегрирования (3.13) вдоль струйки тока получаем (q_тр и L_тр равны и, соответственно, сокращаются) :

Q_н – L_тех = g(z₂ – z₁) + U₂ – U₁ + 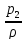-+ (3.14)

Введём в рассмотрение энтальпию газаi = c_pT, гдеc_p–теплоёмкость при постоянном давлении. Из курса термодинамики известно уравнение Майера:

c_p – c_v = R, (3.15)

где c_v – теплоёмкость при постоянном объёме. Далее имеем

c_{v =} с_p – R

U = c_vT = c_pT – RT (3.16)

Используя уравнение состояния (1.1) , запишем уравнение (3.16) в следующем виде:

U = c_pT - 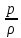=i - 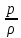(3.17)

Подставляя (3.17) в уравнение энергии (3.14), получаем уравнение энергии в форме энтальпии:

Q_н – L_тех = g(z₂ – z₁) + i₂ – i₁ + (3.18)

Обычно при исследовании процессов в тепловых двигателях изменением потенциальной энергии уровня можно пренебречь. Тогда уравнение энтальпии принимает следующий вид:

Q_н – L_тех = i₂ – i₁ + (3.19)

При отсутствии теплообмена с окружающей средой и технической работы, то есть в случае теплоизолированного течения газа, получаем уравнение энтальпии в следующем виде:

i₂ + = i + (3.20)

откуда следует, что в случае полного торможения потока газа энтальпия достигает максимального значения и обозначается как энтальпия торможения i*, или полная энтальпия:

i* = i + (3.21)

Поскольку i* = c_pT*, то температура T* называется температурой торможения.

Механическая форма уравнения энергии

Запишем уравнение энергии в дифференциальной форме и вычтем из него уравнение первого закона термодинамики:

dQ –dL_тех = dU + gdz + d(pv) + d + dL_тр

-

dQ = dU – pdv

-dL_тех = 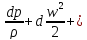gdz + dL_тр (3.22)

[d(pv) – pdv = pdv + vdp – pdv = vdp = ]

Мы получили уравнение энергии в механической форме для элементарной струйки тока. Интегрируя вдоль элементарной струйки, получим уравнение в интегральном виде, которое носит название уравнения Бернулли:

-L_тех = 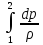++g(z₂ – z₁) + L_тр (3.23)

В Главе второй интеграл Бернулли был нами получен из рассмотрения уравнений Эйлера. В гидравлике и газовой динамике применяется более простая форма уравнения Бернулли, когда техническая работа и работа сил трения равны нулю (L_тех = L_тр = 0). Если рассматривать горизонтальное течение жидкости без потерь, то уравнение (3.23) принимает вид:

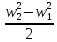+ = 0(3.24)

Если на участке 1 – 2 элементарной струйки плотность жидкости остаётся постоянной, то интеграл в уравнении (3.24) будет равен:

= .

В результате уравнение (3.24) приобретает вид уравнения для идеальной несжимаемой жидкости, полученное Бернулли в 1738 году:

gz₁ + = gz₂ + = const, (3.25)

где gz – напор высоты уровня, – потенциальная энергия уровня (пьезометрический напор), - скоростной напор. Размерность всех членов уравнения (3.25) –

Применение уравнения Бернулли для сжимаемой жидкости связано с вычислением интеграла , которое зависит от вида термодинамического процесса. Предоставляя студенту самостоятельно взять интегралы для изохорического, изобарического и изотермического процессов (что рассматривалось в курсе термодинамики), проведём его вычисление для адиабатического процесса, который имеет наибольшее значение в газовой динамике двигателей. Адиабатический процесс предполагает отсутствие теплообмена с внешней средой.При этом, если имеет место выделение тепла от работы сил трения, то энтропия процесса увеличивается, но сам процесс остаётся адиабатическим. Итак, считаем, что состояние газа изменяется по идеальной адиабате:

= const

Тогда ρ = ρ₁()^1/k

= =^k-1|k-1] (3.26)

Подставляя (3.26) в (3.24), получаем:

–1] + = 0 (3.27)