5.4. Обтекание внешнего тупого угла сверхзвуковым потоком (течение Прандтля - Майера)

Рассмотрим сверхзвуковой поток идеального газа, движущийся вдоль плоской стенки, которая в некоторой точке C делает излом на угол , образуя тупой угол (рис.5.13).

Рис. 5.13. Обтекание тупого угла сверхзвуковым потоком

Вершина угла C является источником слабых возмущений, которые распространяются в сверхзвуковом потоке по прямой линии, наклонённой к направлению потока на угол:

= arc Sin (5.14)

Эта прямая называется характеристикой. Обтекая внешний тупой угол, сверхзвуковой поток расширяется и при этом ускоряется и поворачивается на угол . Этот угол, имеющий конечную величину, можно представить в виде суммы бесконечно малых поворотов. Каждому такому повороту соответствует своя характеристика, наклон которой определяется только числом Маха набегающего потока. В результате образуется семейство характеристик, составляющих сектор с вершиной в точкеC, причём последняя характеристика соответствует скорости повернувшего потока . При повороте сверхзвукового потока около внешнего тупого угла значения скорости, давления и плотности вдоль характеристик остаются постоянными.

При исследовании течения Прандтля – Майера используются полярные координаты, поскольку координатными линиями являются характеристики, выходящие из одной точки C лучами и концентрические окружности с центром в той же точке. Все параметры газа рассматриваются в функции координат Поскольку параметры потока вдоль характеристик не изменяются, то естьа также из-за энергоизолированности течения, когда параметры торможения потока остаются постоянными, задача сводится к определению зависимости λ = λ(). В этом случае параметры потока могут быть определены с помощью газодинамических функций. Поскольку по условию поток является потенциальным безвихревым, то циркуляция скорости по любому замкнутому контуру равна нулю и, в соответствии с теоремой Томсона, не изменяется по времени. Тогда для контура, ограниченного двумя характеристиками и двумя линиями тока (рис. 5.14), можем написать:

Г_ABCD = w_rdr + ()·(r + dr) d= 0

Рис. 5.14. Контур циркуляции скорости

Раскрывая скобки, приводя подобные члены, после сокращения на dr·d получаем:

- = 0 (5.15)

Запишем уравнение энергии в следующем виде:

+ == const (5.16)

Тангенциальная составляющая скорости

(5.17)

Термодинамический процесс обтекания внешнего тупого угла сверхзвуковым потоком считается изоэнтропическим, то есть подчиняющимся уравнению идеальной адиабаты:

= const (5.18)

Уравнения (5.15) – (5.18) составляют систему, к решению которой сводится рассматриваемая задача. Опуская дальнейшие преобразования, приведём искомое решение:

= 1 + (5.19)

Теперь, зная величину коэффициента скорости λ, с помощью таблиц газодинамических функций рассчитать состояние газа на каждой характеристике. Если 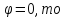λ = 1. По мере увеличения полярного угла скорость газа возрастает, а давление, плотность и температура уменьшаются. Из (5.19) следует, что значение максимальной скорости имеет место в следующем случае:

Sin²() = 1, откуда=(5.20)

Таким образом, для воздуха = 220, а величина

= 130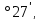так как.

Решение (5.19) получено при условии, что невозмущённый поток движется со скоростью звука (λ_н = 1). Для того, чтобы получить решение для общего случая, когда λ_н 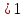, отсчёт углов нужно начинать не от характеристики для λ_н = 1, перпендикулярной к направлению потока, а от некоторой фиктивной характеристики, отстоящей от характеристики данного сверхзвукового потока на фиктивный угол _ф, который определяется из (5.19). Другими словами, считается, что ускорение потока произошло от фиктивной характеристики при _ф = 1, а положение характеристики C – B определяется по формуле (5.14). Соответствующие обозначения показаны на рис. 5.15.

Рис. 5.15. Схема определния характеристик фиктивного потока

После определения характеристики C – B от неё в сторону набегающего потока откладывается угол _ф. Конечный угол _к поворота потока определяется по λ_к.

Физический смысл описанного выше метода расчёта обтекания внешнего тупого угла сверхзвуковым потоком заключается в следующем. Имеется в виду некоторый фиктивный поток со скоростью λ_ф = 1, перпендикулярный характеристике C – A. Этот поток условно разгоняется до скорости λ_н и одновременно поворачивает до горизонтального направления. При этом начальная характеристика поворачивается на угол 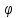_ф. Уравнение линии тока поворачивающегося потока может быть получено, исходя из следующих действий.Общее уравнение линии тока:

=

в полярной системе координат приобретает следующий вид:

=

Опуская вывод, который рекомендуем посмотреть в учебнике Абрамовича, приводим формулу расчёта линии тока в течении Прандтля – Майера в окончательном виде:

r = r₀ (5.21)

Рис. 5.16. Линия тока поворота потока

*Общее название «жидкость» обозначает газ как несжимаемую жидкость и капельную сжимаемую жидкость

Эммиль Микель Викторович

Конспект лекций по курсу «Механика жидкости и газа»

"Газовая динамика"

Подписано в печать Заказ Тираж

Бумага типографская Формат 60´90/16

Машиностроительный университет "МАМИ", Москва, 107023,

Б. Семёновская ул., 38