5.3. Косые скачки уплотнения

Основным отличием косых скачков уплотнения от прямых скачков является расположение фронта скачка, который у косого скачка располагается наклонно к направлению потока. Пересекая фронт косого скачка, поток меняет своё направление. Примерами образования косых скачков уплотнения является обтекание сверхзвуковым потоком клина и конуса.

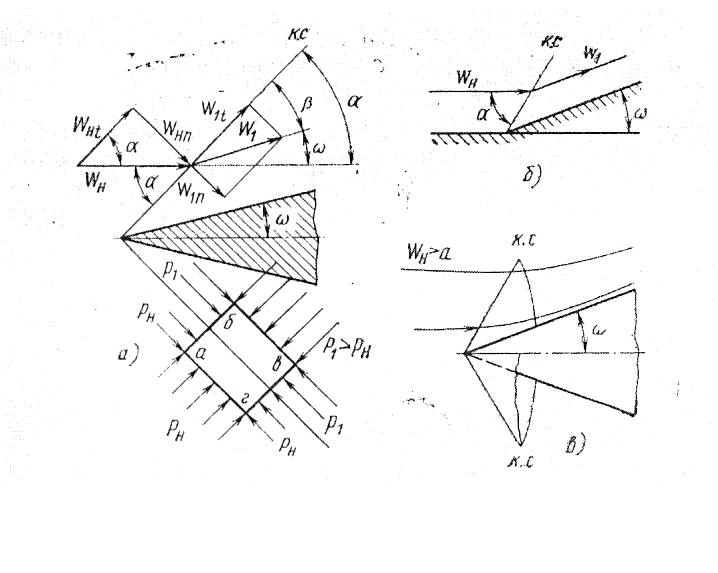
Рис. 5.7. Косой скачок уплотнения; а – схема обтекания клина, б – поворот по тока, в – обтекание конуса

Вектор скорости на рис. 5.7 разложен на две составляющие, направленные по нормали и по касательной к фронту скачка уплотнения. При переходе потока через скачок тангенциальная составляющая скорости остаётся постоянной, а нормальная составляющая уменьшается. Это следует из рассмотрения контура а-б-в-г на рис. 5.7а. Из уравнения количества движения, составленного в проекциях на направление фронта скачка, ввиду равенства давление на поверхностях а-б и г-в следует, что=const. Если же составить уравнение количества движения по нормали к фронту скачка, то ввиду возрастания давления при переходе через скачок (p₁ p_н) нормальная составляющая скорости в косом скачке уменьшается. Таким образом, косой скачок уплотнения сводится к прямому скачку, который сносится вдоль фронта скачка со скоростью w_t.

Косой скачок уплотнения описывается теми же соотношениями, что и прямой скачок, с той лишь разницей, что в индексах скоростей нужно ввести обозначение нормали n, также как и при обозначении температуры торможения. Далее приведём без вывода несколько соотношений для косого скачка уплотнения, поскольку они были получены ранее для прямого скачка уплотнения.

Основное кинематическое соотношение:

= (5.11)

В (5.11) - условная критическая скорость, соответствующая температуре частичного торможения .

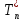В безразмерном виде основное кинематическое соотношение для косого скачка уплотнения имеет вид:

= 1 (5.12)

Основное динамическое соотношение (5.6) и ударная адиабата (5.7) описывают косой скачок уплотнения без каких-либо изменений.

Коэффициент восстановления полного давления описывается по формуле:

= =(5.13)

Отношение статических давлений в косом скачке уплотнения определяется уравнением:

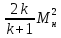= Sin – (5.14)

Как следует из применяемых при расчёте скачков уплотнения выражений (5.9) и (5.14), при одной и той же скорости набегающего потока косой скачок уплотнения всегда слабее прямого скачка. Интенсивность косого скачка уплотнения зависит от угла наклона его фронта к направлению вектора набегающего потока. Здесь имеют место два предельных случая – при косой скачок переходит в прямой, а равенство (5.14) в (5.9). Прикосой скачок вырождается в слабую волну (p_{1 н}), то есть в волну слабых возмущений.

Если в какой-либо точке возникло возмущение, то слабая волна сжатия или разрежения начнёт распространяться из этой точки как из центра во все стороны со скорость звука в данной среде и, таким образом, через определённый промежуток времени t фронт волны будет представлять сферу радиуса ta. Если среда, в которой возникло возмущение, сносится сверхзвуковым потоком со скоростью Образующая конуса называется линией Маха, или характеристикой.

Рис. 5.8. Конус Маха

Угол называетсяуглом слабых возмущений. Из (5.8) следует, что Sin ==.

Таким образом, диапазон изменения угла наклона косого скачка уплотнения определяется следующими пределами:

90≥≥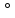

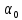
Между углами в косом скачке уплотнения имеется определённая зависимость. Из треугольников скоростей на рис. 5.7 имеем:

=

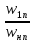Из уравнения неразрывности:

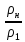= откуда

tg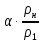= tg = tg(5.9)

Для косого скачка уплотнения известно следующее соотношение:

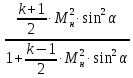= (5.10)

Если теперь подставить (5.10) в (5.9), то получим зависимость между углами

tg (5.11)

Угол отклонения потока в косом скачке уплотнения:

(5.12)

По формулам (5.11) и (5.12) рассчитывается зависимость

(5.13)

На рис.5.9 представлен график этой зависимости, рассчитанный для воздуха (k = 1,4).

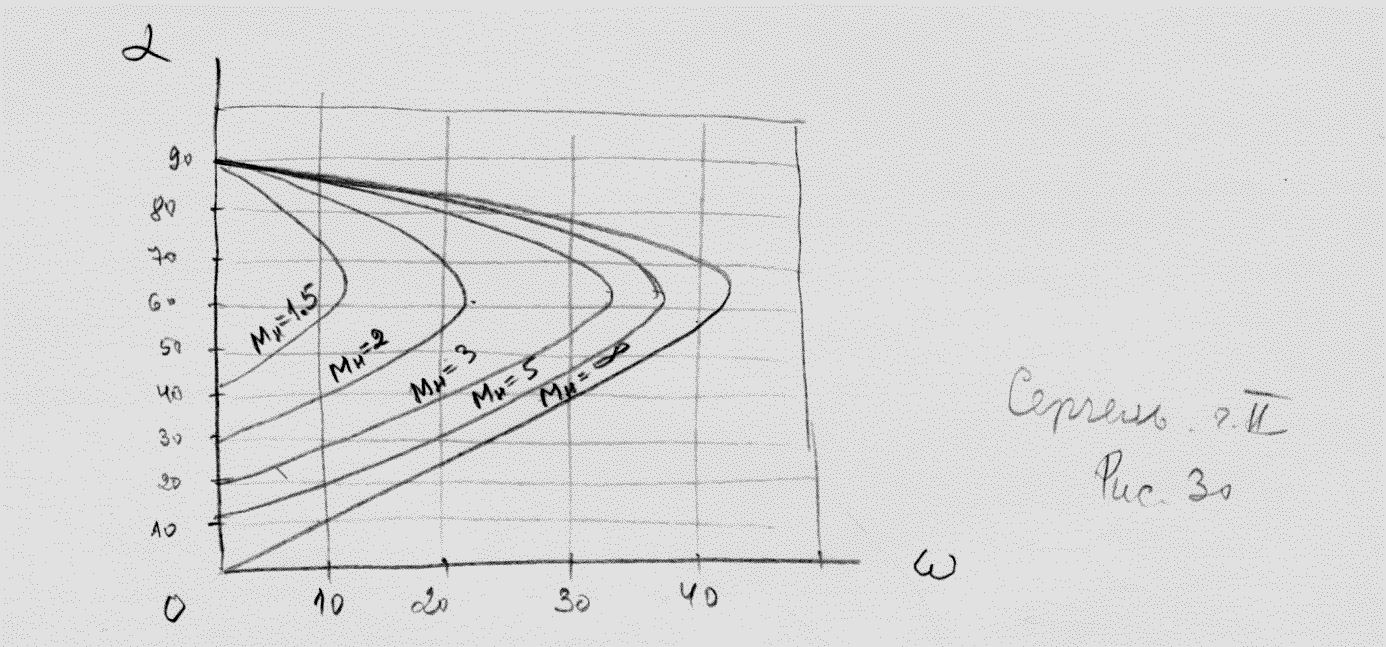
Рис. 5.9. График зависимости

Каждому значению числа Маха набегающего потока соответствует свой предельный угол потока. Например, при числе Маха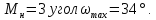При На графике рис.5.9 работают только нижние ветви. После достижения максимального значения угла косые скачки переходят в прямой скачок уплотнения, а все верхние ветви сходятся в точке 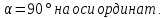Пересечение нижних ветвей с осью ординат соответствует переходу косого скачка уплотнения в слабую волну возмущения, когда угол . Если сверхзвуковой поток обтекает клин с углом, то образуется отошедшая ударная волна, которая в центральной части является прямым скачком уплотнения, а на периферии переходит в косой скачок (рис.5.10).

Скорость за косым скачком уплотнения замедляется, но может оставаться сверхзвуковой. Поворот потока на угол происходит только в дозвуковой зоне. Таким образом, отошедшая головная ударная волна ослабевает от центра к периферии, вырождаясь на периферии в линию слабых возмущений.

Рис. 5.10. Отошедшая головная ударная волна

Решения многих задач на косые скачки уплотнения удобно проводить с помощью ударной поляры. Треугольники скоростей потока с косыми скачками уплотнения (рис. 5.7) можно совместить и построить из одного центра координат. Рассмотрение треугольников скоростей (рис. 5.11) с введением основного кинематического соотношения для косого скачка уплотнения позволяет получить уравнение строфоиды, которая в газовой динамике называется ударной полярой (рис. 5.12).

Рис. 5.11. Треугольники скоростей в косом скачке уплотнения

Рис. 5.12. Ударная поляра

Вектор OB определяет скорость w_н, секущая OCDE пересекает ударную поляру в трёх точках. Отрезок OC соответствует вектору скорости за сильным косым скачком, а отрезок OD – за слабым. Отрезок OE больше отрезка OB и, следовательно, он определял бы скачок разрежения, если бы их существование было возможно. Таким образом, ветви ударной поляры после точки B физического смысла не имеют. Если угол стремится к нулю, то точкаD стремится к точке B, что означает вырождение косого скачка уплотнения в линию слабых возмущений (линию Маха). Если точка C переходит в точку A, то косой скачок превращается в прямой скачок уплотнения (отрезок OA – скорость за прямым скачком). Направление фронта скачка определяется следующим образом. Из точки B через конец вектора w₁ (точки D или C) проводится линия, к которой восстанавливается перпендикуляр из начала координат, который и будет определять фронт скачка уплотнения. Диаграммы ударных поляр имеются в литературе по газовой динамике. Для уменьшения потерь полного давления торможение сверхзвукового потока можно осуществлять в системе косых скачков уплотнения. Этот способ применяется в диффузорах сверхзвуковых самолётов. Профилированная игла в диффузоре обеспечивает возникновение нескольких косых скачков, которые завершаются слабым прямым скачком уже на входе в двигатель. Например, при числе Маха M_н = 2 коэффициент восстановления полного давления 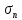= 0,7, то есть потери составляют 30, в то время как реализация системы из двух косых и одного слабого прямого скачков уплотнения обеспечивает всего 4(= 0,96).