5.2. Основное кинематическое и основное динамическое соотношения для прямого скачка уплотнения

Поскольку толщина фронта скачка уплотнения мала, то внешняя механическая работа и вешнее тепло практически не оказывают влияния на процессы внутри фронта скачка. Поэтому течение газа при переходе через скачок уплотнения можно считать энергоизолированным () и, следовательно, можно применять уравнение энергии в форме энтальпии и уравнение импульсов в форме Б.М.Киселёва 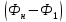. Таким образом, имеем:

Z(λ_н) = Z(λ₁) += λ₁ +

Это уравнение имеет два решения:

1) λ_н = λ₁

2) λ_нλ₁ = 1 (w_нw₁ = )(5.3)

Первое решение не имеет отношения к скачкам уплотнения. Соотношение (5.3) называется основным кинематическим соотношением для прямого скачка уплотнения. Из него следует, что скорость за прямым скачком уплотнения всегда дозвуковая. Очевидно также, что чем больше дозвуковая скорость перед скачком, тем интенсивнее скачок уплотнения.

Связь между параметрами состояния газа перед и за скачком уплотнения устанавливается основным динамическим соотношением, вывод которого даётся ниже.

Умножим правую часть уравнения количества движения (5.1) на комплекс , а левую часть на равную ему величинув соответствии с уравнением неразрывности:

В результате получим следующее уравнение:

(5.4)

Из уравнения энергии имеем:

(5.5)

Приравнивая левые части (5.4) и (5.5), после проведения алгебраических преобразований получим основное динамическое соотношение в следующем виде:

= k (5.6)

Если в (5.6) разделить числитель и знаменатель в левой части на _н, а в правой части на p₁, то после несложных преобразований получим зависимость отношения плотностей от отношения давлений в прямом скачке уплотнения:

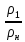= (5.7)

Соотношение (5.7) называется ударной адиабатой. Существенной особенностью ударной адиабаты является то, что при неограниченном возрастании перепада давление в скачке уплотнения увеличение отношения плотностей после и до скачка стремится к пределу, который в соответствии с (5.7) равен:

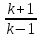= (5.8)

Для воздуха (k = 1,4) эта величина равна 6 (= ). Это означает, что увеличение плотности воздуха в максимально сильном скачке уплотнения не может быть больше, чем в шесть раз. В отличие от ударной адиабаты увеличение плотности потока по идеальной адиабате с ростом давления не имеет предела. На рис. 5.3 показано протекание кривых изменения отношения плотностей после и до скачка уплотнения от перепада давлений на скачке.

Рис. 5.3. Кривые отношений плотностей в зависимости от отношения давлений при сжатии в прямом скачке уплотнения и по идеальной адиабате

Изменение статического давления при переходе через прямой скачок уплотнения можно представить в функциях коэффициента скорости λ и числа Маха M перед скачком. Запишем баланс массовых расходов до и после скачка в следующем виде:

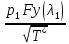G = m = m(5.9)

Учитывая, что величины m, F, при переходе через скачок уплотнения остаются постоянными, получим:

= ==;

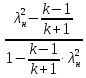Используя формулу связи между числами M и λ, получим в окончательном виде соотношение для отношения статических давлений после и до прямого скачка уплотнения:

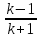= –(5.9)

Для воздуха соотношение (5.9) принимает вид:

= -

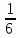
На графиках рис. 5.4 и рис. 5.5 показано протекание кривых ударной адиабаты и изоэнтропы в p –v и T – S координатах.

Рис. 5.4. Кривые ударной и идеальной адиабаты в p – v координатах

Рис. 5.5. Кривые ударной и идеальной адиабаты в T - S координатах

Как уже отмечалось, при бесконечном повышении давления в прямом скачке уплотнения удельный объём уменьшается в 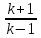раз. Прохождение газа через скачок уплотнения не является изоэнтропическим процессом, поскольку сопровождается необратимым переходом механической энергии в энергию тепловую. Из курса термодинамики известно, что при наличии необратимых процессов энтропия системы возрастает и чем интенсивнее скачок уплотнения, тем больше увеличение энтропии и тем больше потери полного давления при переходе через скачок. Формулу для расчёта потерь полного давления можем получить из баланса расходов до и после скачка уплотнения (5.9), которая имеет следующий вид:

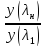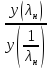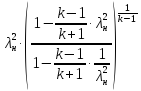= ===(5.10)

Из (5.10) следует, что при λ = 1 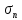= 1, то есть потерь нет посколку нет и скачка уплотнения. График изменения величины коэффициента восстановления полного давления в функции λ_н показан на рис. 5.5. Из этого графика следует, что при небольших сверхзвуковых скоростях потери в прямом скачке уплотнения сравнительно малы, и только после сильно возрастает.

Рис. 5.6. График изменения от величины скорости перед скачком