Fizika_tyazhelykh_ionov

тоны осциллируют в одном направлении, а нейтроны — в противоположном. Эти векторные осцилляции могут возникать при поглощении ядром одного фотона. Более высокие возбуждения включают двойные гигантские дипольные резонансы, а также квадрупольные резонансы, для возбуждения которых требуется поглощение нескольких фотонов. Эти состояния обычно распадаются путем испускания одного или нескольких нейтронов, которые детектируются калориметром «нулевых углов».

9.5.2. Двухфотонные взаимодействия

Двухфотонные процессы интенсивно изучались на e+e− -коллайдерах (LEP, KEK). Поскольку фотоны связаны с зарядами, то измерение выходов мезонов ( qq ), гибридов ( qqg ) и 4- кварковых состояний qqqq позволяет исследовать их кварковое

содержание.

Условие когерентности ограничивает сверху энергии фотонов: 3 ГэВ для RHIC и ~ 150 ГэВ для LHC. Определим дифференциальную светимость

260

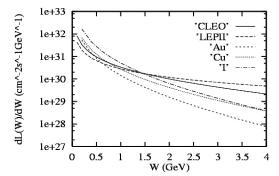
На рис. 9.45 изображены двухфотонные светимости для трех типов ядер, которые предполагается ускорять на RHIC. Как видно, наибольшая светимость для Ι +Ι взаимодействий. Меньший заряд йода по сравнению с золотом компенсируется большей ядерной светимостью и меньшим радиусом.

Рис. 9.45. Двухфотонные светимости для условий RHIC

Для того чтобы вычислить сечение рождения различных частиц в γγ-столкновениях, необходимо знать светимость и сечение образования заданного конечного состояния. Так, сечение образования резонанса массы M R , спина J, полной ширины Γ и двухфотонной

ширины Γγγ :

Формула Брейта–Уиллера для сечения рождения лептонных пар:

261

σ(γγ → e+e− )=

где M — масса лептона.

Сечение образования состояния R в реакции A + A → A + A + R

σ(A + A → A + A + R)= ∫∫F (w,Y )σγγ (w)dwdY . (9.138)

Сечения рождения различных состояний и ожидаемая статистика на год работы ( ~ 107 с) RHIC для различных сталкивающихся ядер представлена в табл. 9.3.

Таблица 9.3

Видно, что для большинства мезонов ожидается статистика в 105 ÷107 событий в год для Au + Au и I + I взаимодействий.

262

9.5.3. Гамма-померонные взаимодействия

Концепция померона существует в физике сильных взаимодействий уже более 30 лет, однако его природа до сих пор неясна. Считается, что померон — бесцветный (в отличие от глюонов) переносчик сильных взаимодействий с вакуумными квантовыми чис-

лами J P = 0++ . В одних процессах (с малыми виртуальностями Q2 ) проявляются свойства «мягкого» померона, в других (при больших Q2 ) — «жесткого» померона. Однако очевидно, что это, скорее

всего, один и тот же объект. «Мягкий» померон связан с поглощательной (неупругой) частью ядерного сечения. При гаммапомеронном взаимодействии фотон можно рассматривать как состояние «голого» фотона плюс различные qq -флуктуации. Когда

ядро поглощает «голый» фотон, qq -флуктуации становятся доминирующими. Пара qq упруго рассеивается на ядре, и образуется

реальный векторный мезон. Эта картина достаточно точно описывает многие реакции, например, упругое pp-рассеяние, гаммапротон взаимодействия на HERA, μN -процессы в Fermilab.

«Жесткий» померон обычно трактуется как состояние двух или более глюонов. Концепция «жесткого» померона используется для описания жестких процессов, например, образование струй с большими поперечными импульсами. В настоящее время непонятно, как соотносятся представления о «мягком» и «жестком» помероне. Так как структура померона не ясна, сечения рождения частиц в γP -взаимодействиях вычислить «из первых принципов» не

удается. Однако можно получить разумные оценки, экстраполируя данные по рождению векторных мезонов в гамма-протонных взаимодействиях на ускорителе HERA. Эти данные интерпретируются

вмодели векторной доминантности: фотон флуктуирует в виртуальный векторный мезон, который упруго рассеивается на протоне. Упругое же рассеяние осуществляется обменом «мягким» помероном.

Сечение рождения векторного мезона слабо зависит от энергии

всистеме центра масс γP-столкновения

263

Для экстраполяции на случай ядро-ядерных взаимодействий сделаем следующие предположения:

а) факторизация вершин взаимодействия (Pp- или Pяд- ро-вершины не зависят от γP-вершины);

б) померон связан со всеми нуклонами ядра, но из-за деструктивной интерференции нет вклада от нуклонов внутри ядра: константа связи померона с ядром пропорциональна числу нуклонов

на поверхности ядра, т. е. ~ А23 ;

в) t-зависимость γP-сечения трактуется как протонный формфактор.

Из-за ядерного форм-фактора нужно рассматривать передачу импульса t между протоном (или ядром) и фотоном. Тогда сече-

где константы AV , b зависят от типа векторного мезона (ρ, ω, φ или J / ψ ). Энергетическая зависимость полного сечения учтена с

264

Величины AV0 и b для различных мезонов приведены в табл. 9.4.

Сечение взаимодействия гамма-ядро получается аналогично, используя ядерный форм-фактор:

Как обычно, ядерный форм-фактор является фу- рье-преобразованием ядерной зарядовой плотности и может быть аппроксимирован следующей функцией:

Тогда ядерное сечение рождения векторного мезона в ультрапе-

ния рождения векторных мезонов в Au+ Au столкновениях при энергиях RHIC, вычисленные по формулам (9.131)–(9.144), содержатся в табл. 9.5.

265

Сечения достаточно велики, учитывая светимость ускорителя, получаем скорость рождения ρ0 , ω, φ соответственно 28, 2.7 и 0.9

Гц. Отметим, что кроме одиночных векторных мезонов, возможно и образование мезонных пар.

Заметим также, что γp -взаимодействия можно выделить на фоне γγ-взаимодействий по быстротному распределению конечных частиц. Константа связи фотона с ядром ~ 1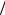K (K — энергия фото-

на), в то время как константа связи померона с ядром не зависит от энергии померона. Поэтому γp -взаимодействия охватывают более

широкий интервал быстрот, чем γγ-взаимодействия.

9.5.4.Померон-померонные взаимодействия

Вкогерентных ядро-ядерных столкновениях возможны и двух-

померонные взаимодействия. Из-за малого размера померона ( ≈1 фм ) эти взаимодействия происходят в узком интервале при-

цельных параметров 2R + 2 > b > 2R . Экспериментальные данные по PP-взаимодействиям в столкновениях α-частиц получены на

ISR.

Сечения PP для αα примерно в 11 раз больше, чем в протонпротонных взаимодействиях при тех же энергиях. В пересчете на полное сечение, сечение PP составляет 0.2%. В случае Au+ Au столкновений доминируют γγ и γp-взаимодействия, в то время как для протон-протонных основным процессом будет поме- рон-померонное взаимодействие. В модели «мягкого» померона трудно объяснить данные по двухпомеронным взаимодействиям, необходимо привлекать представления о «жестком» помероне. Новые данные с ускорителей RHIC и LHC представляют огромный интерес с точки зрения когерентных ядро-ядерных взаимодействий и выяснения природы померона.

266

9.5.5.Интерференционные эффекты

вкогерентных ядро-ядерных взаимодействиях

Как в гамма-гамма, так и в гамма–померонных взаимодействиях начальное состояние одно и то же: два тяжелых ядра. При этом много конечных состояний рождается через более чем одно промежуточное состояние. Как обычно в квантовой механике, возникает возможность интерференции нескольких каналов. Изучение интерференционных эффектов является одной из самых интересных задач физики ультрапериферических столкновений тяжелых ионов.

Примером могут служить процессы γγ → e+e− и γP →V → e+e− ,

где V — векторный мезон. Поскольку γγ- и γp-состояния имеют противоположные C-четности, из-за интерференции конечное состояние будет антисимметричным при замене импульса электрона на импульс позитрона. Интерференция в ρ, ω, φ-мезонах изучалась

в нескольких экспериментах [9.70]. В этих экспериментах пучок фотонов рассеивался на легких (бериллий, углерод) мишенях и измерялось число событий, в зависимости от инвариантной массы конечного состояния в которых электрон имеет больший импульс, чем позитрон. В эксперименте STAR на RHIC будут рассматри-

ваться и другие интерференционные каналы: γγ → π+π− , γp → ρ0 → π+π− , а также γγ → K +K − и γp → φ → K +K − . Как показано в работе [9.71], интерференционные эффекты подавляют выход e+e− - или π+π− -пар в области очень малых значений поперечного импульса пары (p ≤10 ÷20МэВ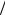с). Очевидно, требуется

очень прецизионная техника детектирования событий с малыми

p .

В заключение этого раздела отметим, что изучение когерентных ультрапериферических столкновений ядер предполагает отбор событий, в которых ядра остаются в основном состоянии или испытывают возбуждения, не приводящие к развалу ядер. Такой отбор осуществляется специальными триггерами, например, в эксперименте STAR на RHIC — c ощью калориметра нулевых углов и центрального баррельного калориметра.

267

CПИСОК ЛИТЕРАТУРЫ

9.1.Chodos A. et al. // Phys. Rev. D. 1974. V. 9. P. 3471.

9.2.Landau L., Lifshitz E. // Statistical Physics, Pergamon Press, 1986.

9.3.Morley P., Kislinger M. // Phys. Rep. 1979. V. 51. P. 65.

9.4.Belavin A. et al. // Phys. Lett. B. 1975. V. 59. P. 85.

9.5.Shuryak E. // Nucl. Phys. B. 1982. V. 203. P.160.

9.6.Shifman M., Vainshtein A., Zakharov V. // Nucl. Phys. B. 1979. V. 147. P. 385.

9.7.Bochkarev A., Shaposhnikov M. // JETP Lett. 1984. V. 39. P. 488.

9.8.Bochkarev A., Shaposhnikov M. // Nucl. Phys. B. 1986. V. 268. P. 220.

9.9.McLerran L, Svetitsky B. // Phys. Rev. D. 1983. V. 24. P. 237.

9.10.Kajantie K. et al. // Z. Phys. C. 1981. V. 9. P. 253.

9.11.Banks T., Ukawa A. // Nucl. Phys. B. 1983. V. 225. P. 145.

9.12.Karsch F. // arXiv:0711.0661 [hep-lat]

9.13.Cheng M. et al. // 0710.0354v1 [hep-lat]

9.14.DeTar C., Gupta R. // PoS (LATTICE2007). P. 179.

9.15.Karsch F. // Nucl. Phys. B. 2000. V. 83–84. P. 14

9.16.De Forcrand Ph. et al. // Phys. Rev. D. 2001. V. 63. P. 054501

9.17.Karsch F. et al. // Nucl. Phys. A. 2003. V. 715. P. 701.

9.18.Karsch F. // Lecture Notes Phys. 2002. V. 583. P. 209

9.19.Fodor Z. et al. // J. High En. Phys. 2002. V. 203. P. 14.

9.20.Iancu E., Leonidov A., McLerran L. // Nucl. Phys. A. 2001. V. 692. P. 583.

9.21.Schildknecht D., Surrow B. // Phys. Lett. B. 2001. V. 499. P. 116; Stasto A. et al.

// Phys. Rev. Lett. 2001. V. 86. P. 596.

9.22.Cleymans J., Gavai G., Suhonen J. // Phys. Rep. 1986. V. 102. P. 140.

9.23.Bjorken J. // Phys. Rev. D. 1983. V. 27. P. 140.

9.24.Hwa R., Kajantie K. // Phys. Rev. D. 1985. V. 32. P. 1109.

9.25.McLerran L., Toimela T. // Phys. Rev. D. 1985. V. 31. P. 545.

9.26.De Forcrand P., Philipsen O. // Nucl. Phys. B. 2002. V. 642. P. 290.

9.27.Stock R. // Phys. Lett. B. 1999. V. 456. P. 277.

9.28.Schmidt M. et al. // Z. Phys. C. 1988. V. 38. P. 109.

9.29.Combridge B. // Nucl. Phys. B. 1979. V. 151. P. 429.

9.30.Eskola K., Kajantie K. // Z. Phys. C. 1997. V. 75. P. 515.

9.31.Емельянов В., Ходинов А. и др. // Ядерная Физика. 1999. Т. 62. С. 62.

9.32.Adler C. et al. // Nucl. Instrum. Meth. A. 2001. V. 470. P. 488

9.33.Adcox K. et al. // Phys. Rev. Lett. 2001. V. 86. P. 3500.

9.34.Van Hove L. // Z. Phys. C. 1983. V. 21. P. 93.

9.35.Ruuskanen P. // Nucl. Phys. A. 1991. V. 525. P. 255c.

9.36.Gale C., Lichard P. // Phys. Rev. D. 1994. V. 49. P. 3348.

9.37.Song C., Ko C., Gale C. // Phys. Rev. D. 1994. V. 50. P. 1827.

9.38.Lichard P. // Phys. Rev. D. 1994. V. 49. P. 5812.

9.39.Matsui T., Satz H. // Phys. Lett. B. 1986. V. 178. P. 446.

9.40.Geiss J. et al. // Phys. Lett. B. 1999. V. 447. P. 31; Spieles C. et al. // Phys. Rev. C. 1999. V. 60. P. 054901; Arwesto N. et al. // Phys. Rev. C. 1999. V. 59. P. 395.

9.41.Pisarski R. // Phys. Lett. B. 1982. V. 110. P. 155.

9.42.Rapp R., Wambach J. // Adv. Nucl. Phys. 2000. V. 25. P. 1.

268

9.43.Gale C., Kapusta J. // Phys. Rev. C. 1989. V. 40. P. 2397.

9.44.Agakichiev G. et al. // Nucl. Phys. A. 1999. V. 661. P. 23c.

9.45.Acton P. D. et al. // Z.Phys. C 56 (1992), 521; Buskulic D. et al. // Z.Phys. C 69 (1996), 379.

9.46.Aguilar-Benitez M. et al. // Z. Phys. C. 1991. V. 50. P. 405.

9.47.Adams J. et al. // Phys. Rev. Lett. 2004. V. 92. P. 092301.

9.48.Reygers K. // nucl-ex/0608043.

9.49.Muller B. // Lect. Notes in Phys. 1985. V. 225. P. 1.

9.50.Meyer-Ortmanns H. // Rev. Mod. Phys. 1996. V. 68. P. 512.

9.51.Rafelski J., Muller B. // Phys. Rev. Lett. 1983. V. 48. P. 1006.

9.52.Datta S., Karsch F. et al. // hep-lat/0208012.

9.53.Shuryak E., Zahed I. // hep-ph/0307267.

9.54.Elze H., Greiner W. // Phys. Lett. B. 1986. V. 131. P. 385.

9.55.Koch P., Muller B., Rafelski J. // Phys. Rep. 1986. V. 142. P. 167.

9.56.Emelyanov V. // Pisma Zh. Eksp. Teor. Fiz. 1988. V. 47 No. 1. P. 491.

9.57.Busching H. // Eur. Phys. J. C. 2005. V. 43. P. 303; Adams J. et al. // Phys. Rev. Lett. 2003. V. 91. P. 172302; Adler S. S. et al. // nucl-ex/0503003

9.58.Adams J. et al. // Phys. Rev. Lett. 2003. V. 91. P. 072304

9.59.Schnederman E. at el. // Phys. Rev. D. 1993. V. 48. P. 2462.

9.60.Voloshin S. and Zhand Y. // Z. Phys. C. 1996. V. 70. P. 665.

9.61.Barrette J. et al. // Phys. Rev. C. 1994. V. 49. P. 1669.

9.62.Cugnon J., Hote D. // Nucl. Phys. A. 1986. V. 452. P. 138.

9.63.Danielewicz P. // Phys. Rev. C. 1995. V. 51. P. 716.

9.64.Siemens P., Rassmussen J. // Phys. Rev. Lett. 1979. V. 42. P. 880.

9.65.Shuryak E., Zhirov O. // Sov. J. Nucl. Phys. 1978. V. 28. P. 485.

9.66.Adler S.S. et al. // Phys. Rev. Lett. 2006. V. 96. P. 032302; Adams J. et al. // Phys. Rev. Lett. 2004. V. 92. P. 052302; Adams J. et al. // Phys. Rev. Lett. 2005. V. 95. P. 122301.

9.67.Lacey R. A., Taranenko A. // nucl-ex/0610029v3

9.68.Kovtun P., Son D. T., Starinets A.O. // Phys. Rev. Lett. 2005. V. 94. P. 111601.

9.69.Drees M., Ellis J., Zeppenfeld D. // Phys. Lett. B. 1989. V. 223. P. 454.

9.70.Bauer T. H. et al. // Rev. Mod. Phys. 1978. V. 50. P. 261.

9.71.Klein S., Nystrand J. // Phys. Rev. Lett. 2000. V. 84. P. 2330.

269