2.3. Геометрическое изображение линейной функции (градиент и линии уровня)

Зафиксируем значение , получим уравнениепервой степени с двумя переменными, которое геометрически задает прямую. В каждой точке данной прямой функция принимает одно и то же значениеи являетсялинией уровня. Придавая различные значения, например,, ... , получим множество линий уровня, которые образуютсовокупность параллельных прямых.

Для линейной функции градиент – это вектор , координаты которого равны частным производным функциипои по(значениям коэффициентов при переменных в целевой функции). Данный вектор перпендикулярен каждой прямой (линии уровня)и показывает направление возрастания целевой функции.

Пример 4. Построить линии уровня и градиент функции .

Линии уровня при ,,- это прямые,,,параллельные друг другу.

Градиент – это вектор , перпендикулярный каждой линии уровня.

2.4. Графическое нахождение наибольшего и наименьшего значений линейной функции в области

Геометрическая постановка задачи. Найти в области решений системы линейных неравенств точку, через которую проходит линия уровня, соответствующая наибольшему (наименьшему) значению линейной функции с двумя переменными.

Последовательность действий:

1. Построить область допустимых решений системы линейных неравенств Если область непустая, то можно говорить о целесообразности нахождения в ней наибольшего и наименьшего значений функции.

В

A

2. Построить градиент и одну из линий уровня функции .

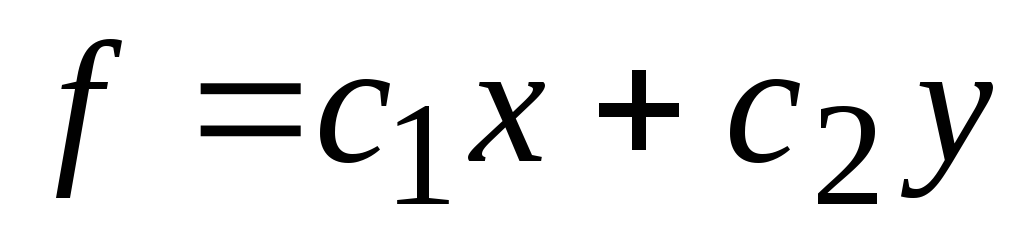3. Параллельным перемещением прямой в направлении векторагеометрически найти две точки:

• точку А «входа» в область. Эта точка определяет точку наименьшего значения функции ;

• точку В «выхода» из области. Эта точка определяет точку наибольшего значения функции .

4. Найти координаты точки А, решая систему уравнений прямых, пересекающихся в точке А. Вычислить наименьшее значение функции . Аналогично - для точки В и наибольшего значения функции.

Пример 5. Найти наибольшее и наименьшее значения функции

в области решений системы линейных неравенств

Решение

1. Построим область решений системы линейных неравенств.

у

1

О 2 x

Прямая (), точки для построенияи. Так какверно, то полуплоскость обращена в сторону точки.

Прямую ()строим по точками; неравенствоверное, полуплоскость направлена к началу координат.

Прямая ()построена по точками; полуплоскость обращена в сторону.

Неравенства ипоказывают, что искомая область (пересечение всех полуплоскостей) находится в первой координатной четверти.

2. Построим градиент функции . Это вектор с координатамис началом в точке. Перпендикулярно градиенту построимодну из линий уровня.

3. Параллельным движением линии уровня в направлении градиента найдем точку «входа» линии уровня в область – это точка О(0,0). Вычислим значение функции в этой точке: .

4. Продолжая движение линии уровня в направлении градиента , найдемточку «выхода» линии уровня из области – это точка А. Для определения ее координат решим систему уравнений прямых и:Решение системы уравненийи. Вычислимзначение функции в точке :.

Ответ: ,.