3. Частные производные

Ограничимся случаем функции двух переменных (для большего числа переменных аналогично).

• Пусть функция определена в окрестности точки. Придадим переменной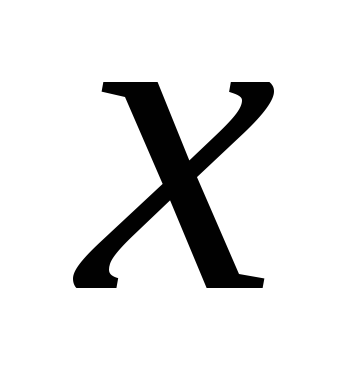в точкеприращение, оставляя значение переменнойнеизменным. Соответствующее приращение функции

называется частным приращением функции по переменной в точке.

Аналогично определяется частное приращение функции по переменной :.

• Частной производной функции двух переменных по переменнойв точке называется конечный предел отношения частного приращения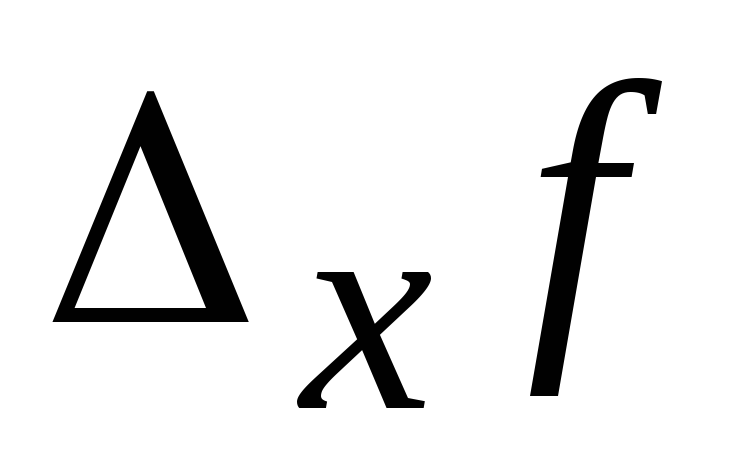функции по переменной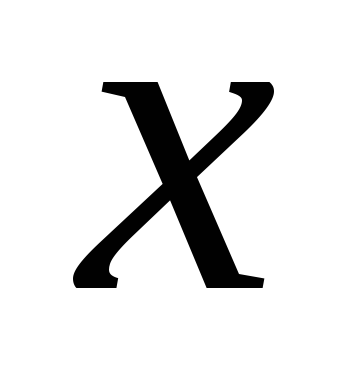к приращению этой переменнойпри стремлении к нулю приращения: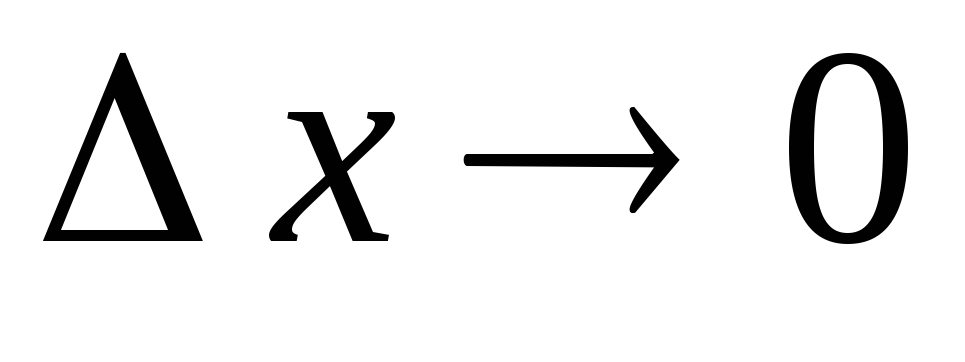

.

Обозначается частная производная по символами:,,,.

• Частной производной функции по переменнойназывается предел:

.

Обозначения: ,,,.

Частные производные можно рассматривать как скорости изменения функции относительно одной из переменных (в направлении соответствующей оси координат). Для нахождения частной производной по переменнойиспользуются правила дифференцирования функции одной переменной,считая переменную постоянной.. Аналогично, для нахождения частной производной по переменнойпостоянной считается переменная .

Пример 4. Для функции найти частные производные,и вычислить их значения в точке.

Решение

Частная производная функции по переменнойнаходится в предположении, чтопостоянна:

.

Найдем частную производную функции по , считая постоянной:

.

Вычислим значения частных производных при ,:

; .

4. Частные производные высших порядков

Введем понятие частных производных высших порядков.

Пусть функция имеет частные производные ив точкеи в каждой точке окрестности точки.

• Частными производными второго порядка функции нескольких переменных называются частные производные от частных производных первого порядка.

Запишем для все частные производные второго порядка:

; ;

; .

Аналогично определяются и обозначаются частные производные третьего порядка, например:

; и т.д.

• Производные, взятые последовательно по разным переменным, называются смешанными частными производными. Для функции двух переменных смешанные частные производные есть ,.

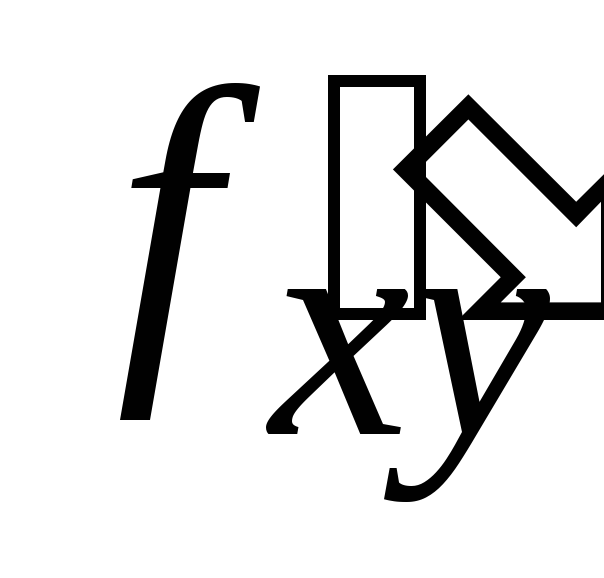• Теорема. Если смешанные частные производные функции нескольких переменных непрерывны в некоторой точке , то они равны между собой в этой точке.

Для функции двух переменных значения смешанных частных производных не зависят от порядка дифференцирования:

.

Пример 5. Для функции найти частные производные второго порядкаи.

Смешанная частная производная находится последовательным дифференцированием сначала функциипо(считаяпостоянным), затем дифференцированием производнойпо(считаяпостоянным).

=

Производная находится дифференцированием функциисначала по, затем производнойпо.

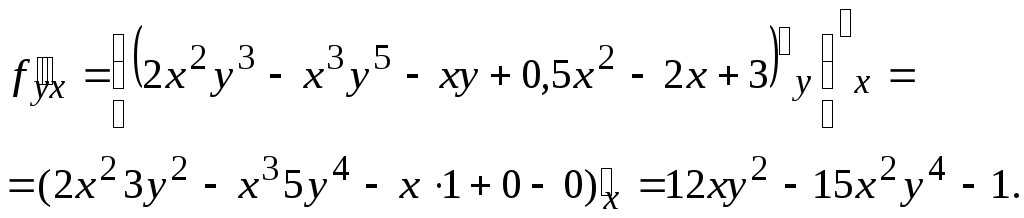
Смешанные частные производные равны между собой: .

5. Дифференциал функции двух переменных и его применение

Рассмотрим функцию двух переменных . Пусть каждый аргумент,получил приращениеии стал равными, т.е. точка«перешла» в точку.

• Приращение функции 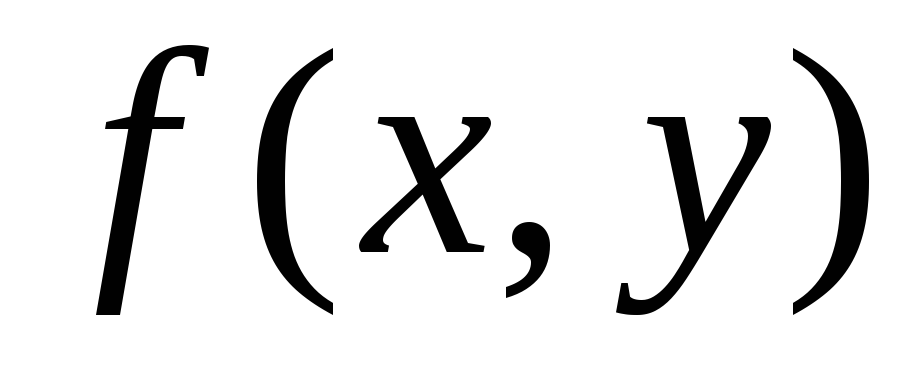по переменными

называется полным приращением функции в точке .

Пример 1. Для функции полное приращение:

Таким образом, в полном приращении функции можно выделить слагаемые, линейные относительно приращений аргументов и:

.

Нетрудно видеть, что коэффициенты при приращениях иесть частные производные функциипои по:

, .

• Часть полного приращения функции, линейная относительно приращений аргументов и, называется полным дифференциалом функции и обозначается : .

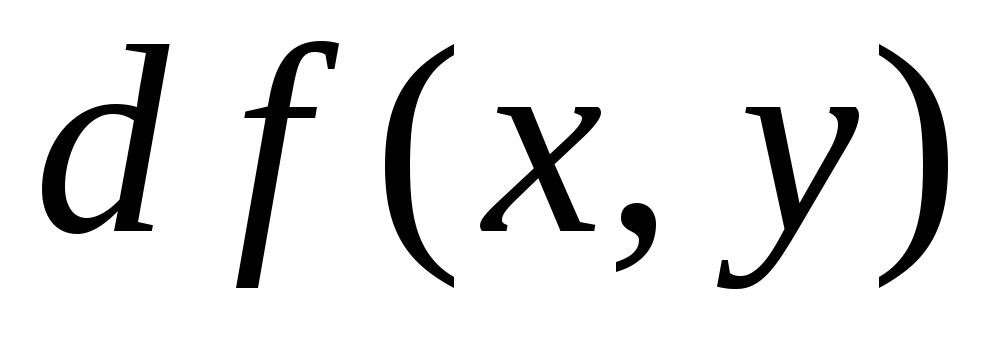Так как для независимых переменных иих дифференциалы равны приращениям,, тополный дифференциал функции равен .

Дифференциал функции равен.

• Функция , имеющая дифференциал в точке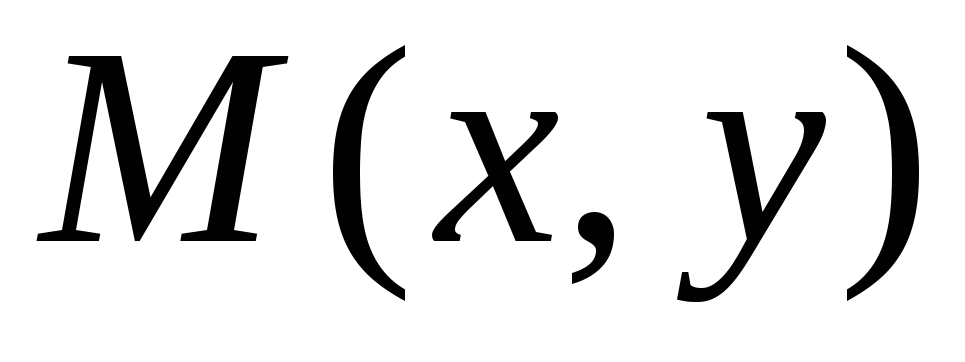, называетсядифференцируемой в данной точке .

Итак, если функция дифференцируема в точке , то она имеет частные производные в этой точке

Пример 2. Полный дифференциал для равен.

Рассмотрим применение полного дифференциала для приближенных вычислений. При малых приращениях аргументов ,полное приращение функции приближенно равно полному дифференциалу:

, или .

Выразим значение функции:

.

Формула «полных приращений» позволяет приближенно вычислить значение функции в точке, если известны значения функции и ее частных производных в ближайшей точке.

Пример 3. Вычислить .

Воспользуемся функцией и вычислим ее значение в точке. Ближайшей точкой является точка, то есть,. Приращение аргументови.

Найдем значения функции и частных производных в точке :

;

; тогда ;

; тогда .

Подставим найденные значения в формулу полных приращений, получим .