Тема 3. Наибольшее и наименьшее значения функции двух переменных в области

Содержание

1. Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой ограниченной области

2. * Нахождение наибольшего (наименьшего) значений линейной функции в области, заданной линейными ограничениями

2.1. Постановка задачи

2.2. Графическое решение системы линейных неравенств

2.3. Геометрическое изображение линейной функции

2.4. Графическое нахождение наибольшего и наименьшего значений линейной функции в области

1. Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой ограниченной области

Постановка задачи. Пусть на плоскости замкнутая ограниченная областьзадается системой неравенств вида. Требуется найтив области точки, в которых функция принимаетнаибольшее и наименьшее значения (глобальный экстремум).

Решение данной задачи опирается на следующую теорему.

Теорема. Пусть функция непрерывна в замкнутой ограниченной области , граница которой является кусочно гладкой (состоит из кусков «гладких на ощупь» кривых или прямых). Тогда в областифункция достигает своего наибольшего и наименьшегозначений.

Порядок нахождения наибольшего и наименьшего значений функции в замкнутой ограниченной области .

1. Строим область ; выделяем все части границы области и находим все «угловые» точки границы.

2. Находим стационарные точки внутри из условия.

3. Найти стационарные точки на каждой границе области .

4. и вычислить значения функции в стационарных точках внутри и на границе области ,

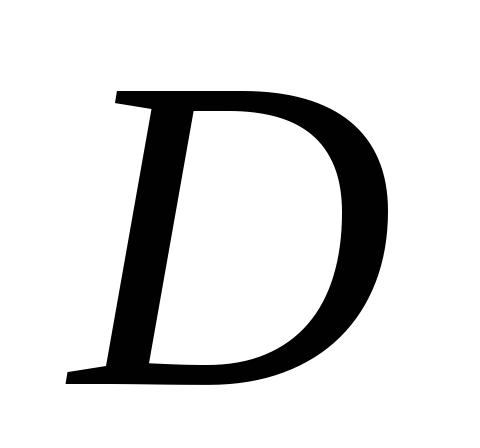5. Вычисляем значения функции во всех стационарных и угловых точках, а затем выбираем наибольшее и наименьшее значения.

Пример 1. Найти наименьшее и наибольшее значения функции в замкнутой области, заданной системой неравенств,,. Сделать чертеж.

Решение

Найдем критические точки, решая систему уравнений . Отсюда

Построим область . Данная область– треугольник. Стационарная точкалежит внутри области.

y

3

()

()

0 () 3x

Найдем критические точки на каждой границе области.

А) Из уравнения прямой выразими подставим в функцию. Получим

.

Критическая точка находится из условия . Отсюда, тогда. Стационарная точкалежит на границе области.

Б) На границе функция принимает вид. Стационарная точка находится из условия. Отсюдаи стационарная точкалежит на границе области.

В) На границе функция принимает вид. Стационарная точка находится из условия. Отсюдаи стационарная точкалежит на границе области.

Итак, имеем стационарные точки: ,,,. Отметим их в области.

Вычислим значения функции в стационарных точках:

;

;

;

.

Выберем среди них наибольшее и наименьшее значения:

; .

2*. Нахождение наибольшего (наименьшего) значений линейной функции в области, заданной линейными ограничениями

2.1. Постановка задачи

Важной является задача нахождения экстремума, математическая модель которой содержит линейные ограничения (уравнения, неравенства) и линейную функцию .

Постановка задачи. Найти наибольшее и наименьшее значения функции (2.1)

при ограничениях

(2.2)

. (2.3)

Поскольку для линейной функции двух переменных нет критических точек внутри области , то оптимальное решение, доставляющее целевой функции экстремум, достигается толькона границе области. Для области, заданной линейными ограничениями, точками возможного экстремума являются угловые точки. Это позволяет рассматривать решение задачи графическим методом.