6. Дифференциал второго порядка

• Дифференциалом второго порядка функции называется дифференциал от дифференциала первого порядка:

.

Пример 4. Для функции найти дифференциал второго порядка.

Найдем частные производные первого и второго порядка:

; ;

; ;;

Дифференциал второго порядка равен

.

7. Градиент функции двух переменных

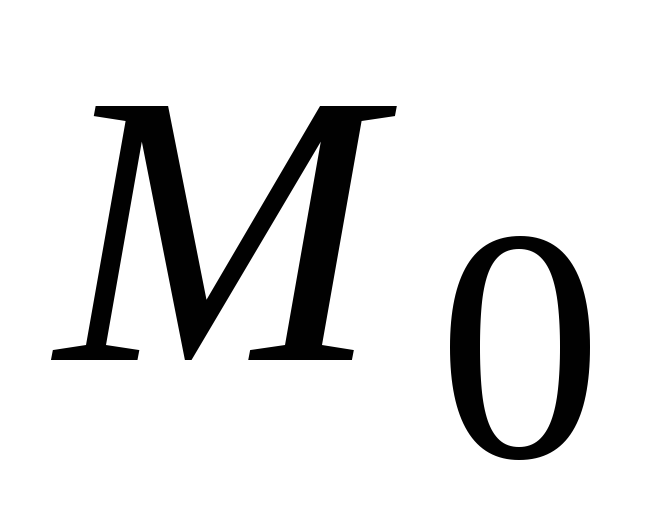• Градиентом функции в точке называется вектор, начало которого – в точке , а координаты равны значениям частных производных в точке: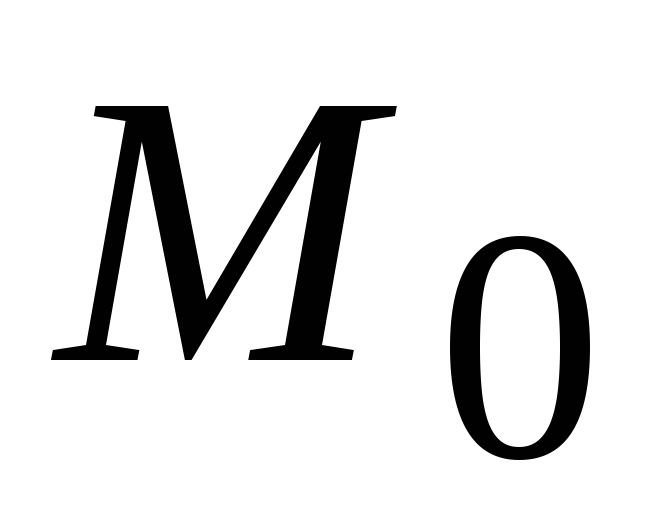

.

Свойства градиента

1. Градиент показывает направление наибольшего возрастания значений функции.

2. Длина вектора градиента равен максимальной скорости изменения функции в направлении градиента.

3. Для функции градиент перпендикулярен линии уровня, проходящей через точку .

Пример 5. Дана функция . Найти градиентв точкеи построить его.

Найдем координаты градиента – частные производные.

.

В точке градиент равен . Начало векторав точке, а конец - в точке.

5

1

0 2 4

Аналогично определяется градиент функции трех переменных :

Контрольные вопросы

1. Дайте определение функции двух переменных .

2. Что является областью определения функции ?

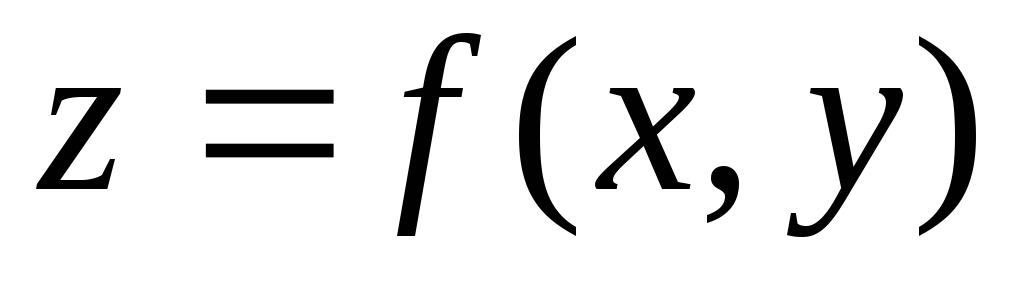3. Что является графиком функции двух переменных ?

4. Графиком какой функции двух переменных является плоскость?

5. Что называется линией уровня функции ?

6. Как расположены линии уровня линейной функции ?

7. Как расположены линии уровня функции ?

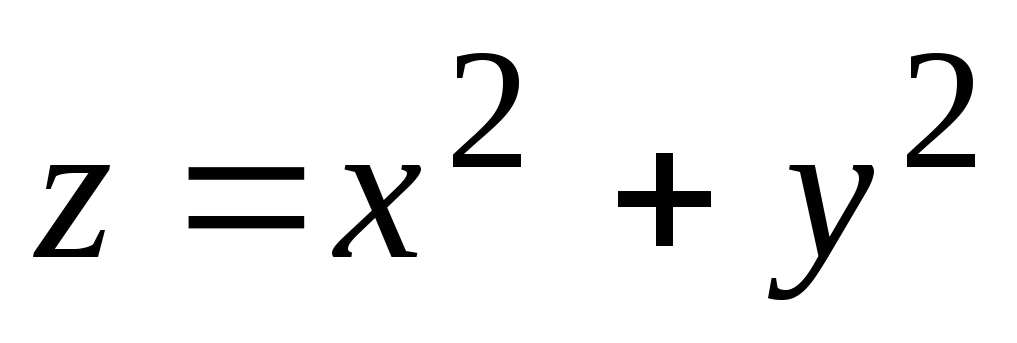8. Запишите частное приращение функции двух переменных по переменной .

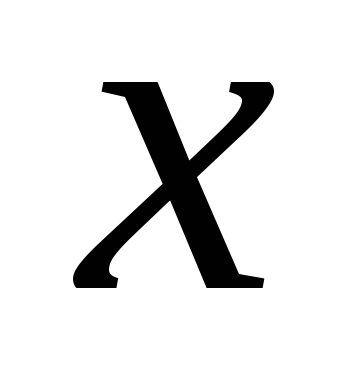9. Как определяется частная производная функции 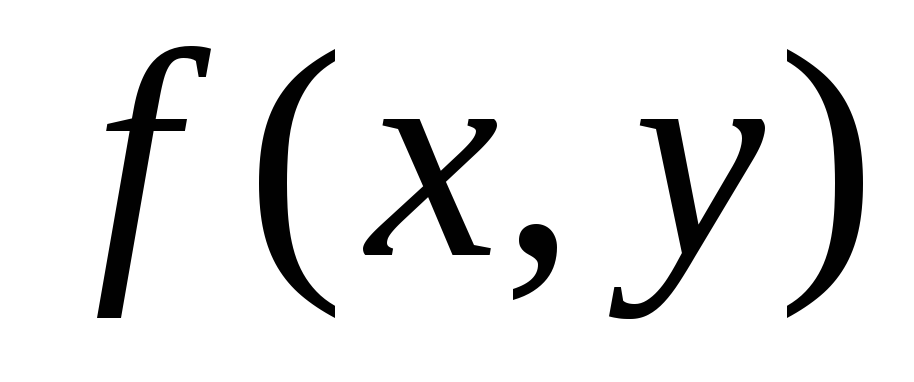по переменной? По переменной?

10. Как вычисляются частные производные?

11. Дайте определение частных производных второго порядка, третьего, 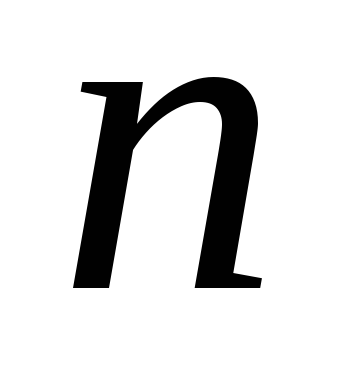-го порядка функции.

12. Что означает символическая запись ?

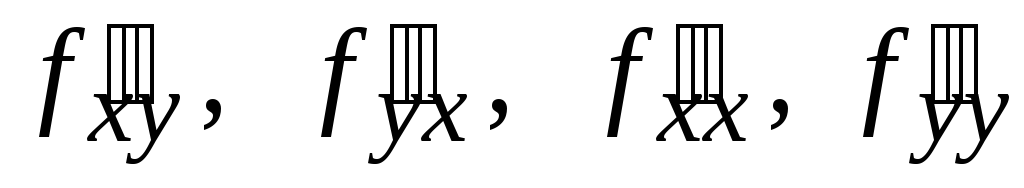13. Сформулируйте свойство смешанных частных производных функций двух переменных.

14. Запишите полное приращение для функций двух переменных.

15. Что называется полным дифференциалом функции ?

16. Как найти полный дифференциал функции ?

17. Запишите формулу для нахождения дифференциала второго порядка функции .

18. Какова связь между полным дифференциалом функции нескольких переменных и ее полным приращением?

19. Сформулируйте свойства градиента.

20. Как расположен градиент функции относительно линий уровня?

Тема 2. Экстремум функции двух переменных

Содержание

1. Локальный экстремум

2. Условный экстремум функции двух переменных

1. Локальный экстремум

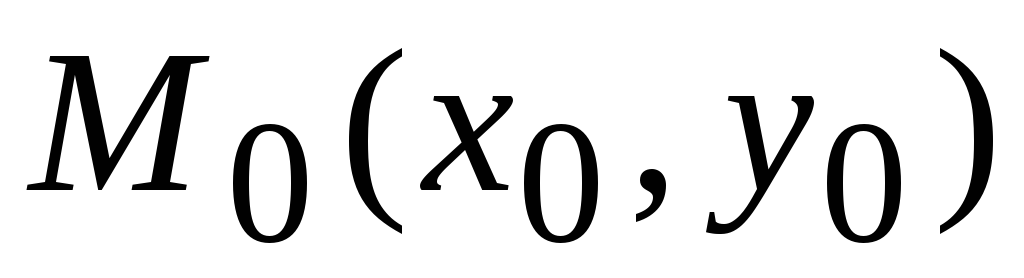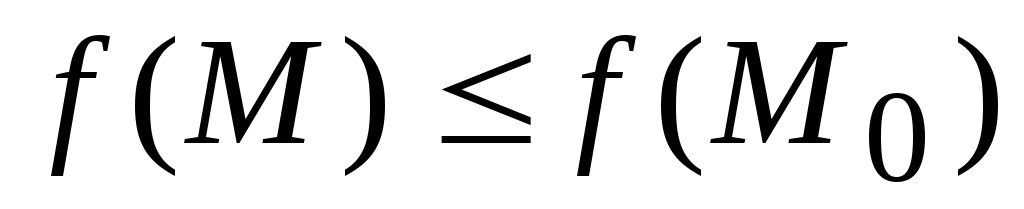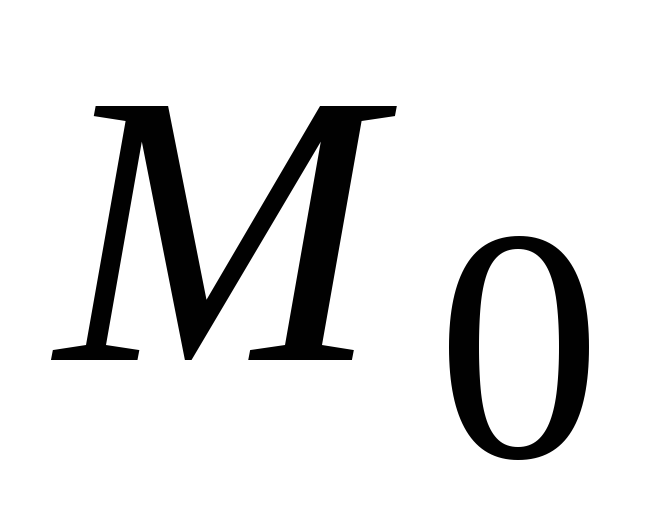• Значение называетсямаксимумом функции двух переменных , если оно является наибольшим в некоторой окрестности точки , т.е. в этой окрестности выполняется неравенство . Точканазываетсяточкой максимума.

• Для минимума функции: .

• Максимумы и минимумы функции называются экстремумами функции.

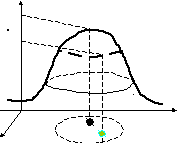
На рисунке точка является точкой максимума функции.

• Точка 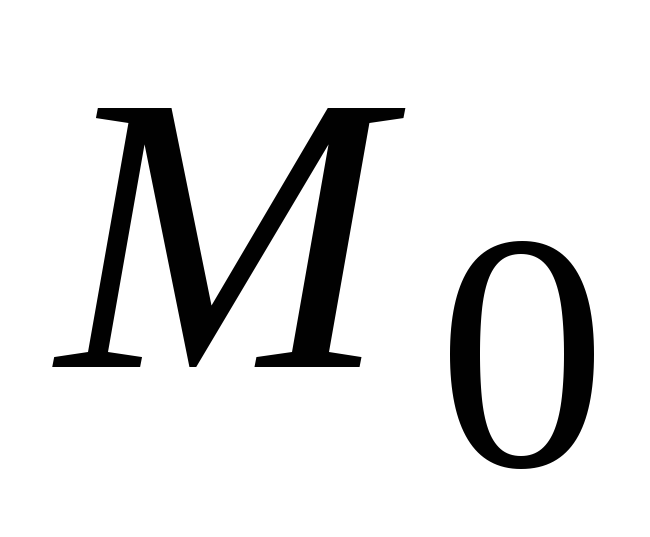называетсястационарной точкой функции , если она является внутренней точкой области определения функции и все частные производные первого порядка в ней равны нулю.

• Точка , в которой частные производные равны нулю или не существуют, называетсякритической точкой функции .

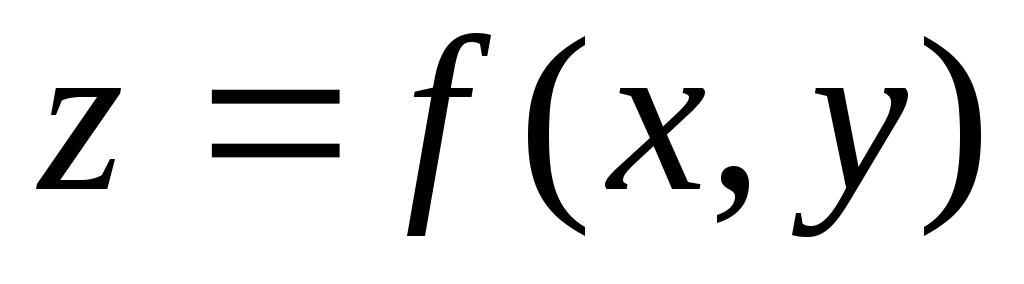Таким образом, точки экстремума следует искать среди ее критических точек.