
Пособие по математической статистике
.pdf
Задача 5
Х генеральная совокупность (дискретная случайная величина)
Получено следующее статистическое распределение
|
Xi |
-4 |
-2 |
|
0 |
|
2 |
3 |
|
ni |
8+n |
3+n |
|
1+n |
|
2 |
3+n |
1. |
Найти область допустимых значений для параметра «n» |
|
|
|||||
2. |
Найти выборочное среднее ̅ |
( ) (функция аргумента n) |
|
|||||
3.Найти предельное значение ̅ при неограниченном увеличении объёма
выборки.
Может ли при большом объёме выборки а) ̅=-2; б) ̅=1?
4.Пусть ̅ . Найти значение параметра n.
5.Для найденного n найти 1)статистический ряд; 2)полигон относительных частот;3)выборочную функцию распределения F*(x); 4)выборочную
дисперсию D*x и выборочное среднее квадратичное отклонение *х;
5)исправленную дисперсию S2и S; 6) p{-1,5≤X≤2}
Решение
1.Область допустимых значений параметра «n»
n>-1 n {0;1;2;…}
{
2.Выборочное среднее
̅= |
∑ |
|
N объём выборки N= |
∑ |
8+n+3+n+1+n+2+3+n=4*n+17 |
|
|
 =4*n+17
=4*n+17
̅= ( ) ( ) ( )=
3.Предельное значение выборочного среднего.
(N ∞ n ∞)
̅=

 = --3/4(предельное значение для выборочного
= --3/4(предельное значение для выборочного
среднего)
Покажем схему графика данной функции ,если n {0;1;2;…}
Стр. 21
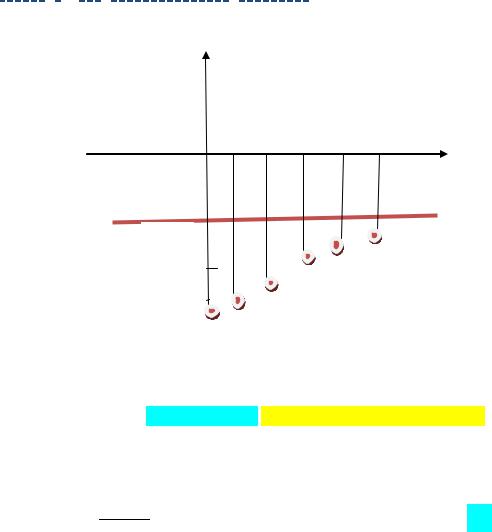
̅(0)=- ≈ , ; ̅( )=-4/3≈-1,3; ̅( ) -31/25=-1,25; ̅( )= -34/29≈-1,17;
̅( )= -37/33≈-1,12; ̅( )= -55/56≈-0,96; ̅(100)= -325/417≈-0,78
Прямая ̅= -3/4 горизонтальная асимптота
̅
n
-3/4
Как видно из построенного графика , множество значений данной функции находится в интервале [-25/17; -0,75) выборочное среднее ̅≠-2; ̅≠1.
4.Нахождение параметра «n»по заданному значению выборочного среднего.
̅=-31/25 = - 25*(-3*n-25)=-31*(4n+17) 49*n=98 n=2
(Заметим, что это значение мы получили раньше при вычислении значения функции в точке n=2)
1)Статистический ряд при n=2
|
Xi |
-4 |
|
-2 |
|
|
0 |
|
2 |
3 |
|
|
ni |
10 |
|
5 |
|
|
3 |
|
|
2 |
5 |
|
|
0,4 |
|
0,2 |
|
|
0,12 |
|
0,08 |
0,2 |
|
|
|
|
|
|
|
|
|
||||
|
Объём выборки N=25 |
|
Контроль: |
∑ |
=1 |
|
|
|
|
||
Стр. 22
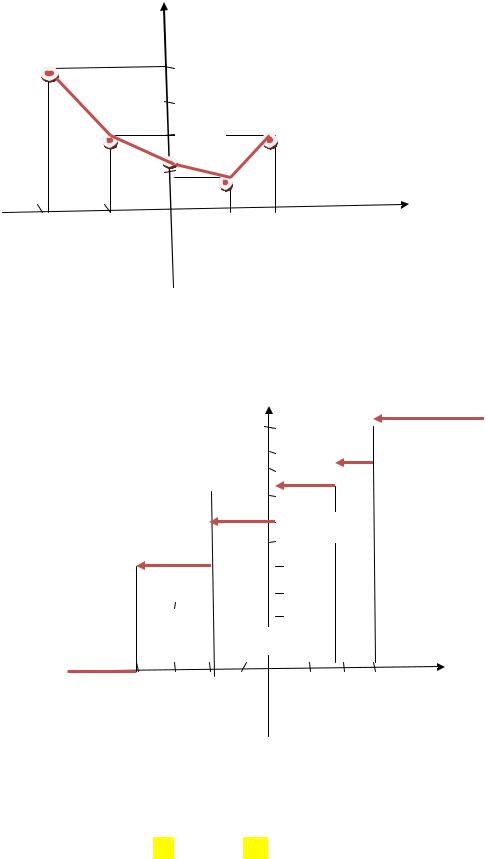
2)Полигон относительных частот
0,4
0,2
-4 |
-2 |
2 |
3 |
х |
|
|
3)Выборочная функция распределения
F*(x)
, |
1 |
F*(x)= ,,
,
[ |
0,6 |
|
|
|
0,1 |
x |
-4 |
-2 |
2 |
3 |
|
|
4)Выборочная дисперсия и выборочное среднее квадратическое отклонение
По условию ̅= -31/25=-1,24
Стр. 23

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Dx*= |
̅̅̅̅ |
-( |
̅ |
) |
2 |
; |
̅̅̅̅ |
=∑ |
|
=9,32 |
|
|
D*x=7,7824; |
|
*x= |
√ |
|
|
≈ ,79 |
|
|||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Отв т: |
D*x=7,7824; |
|
*x≈ |
,79 |
|
|
|
|
|
|
|
|
|||
5)Ис ав |
|
ая с с я |
с |
ав |
с |
|
|
ква |
ат ч ск |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
тк |
. |
|
|
|
|
|
|
|
|
|
||||
S2= *DX* S2= *7,7824≈8,107; S=√ ≈2,847
*DX* S2= *7,7824≈8,107; S=√ ≈2,847
Ответ: S2≈8,107; S≈2,847
6) p{-1,5≤X≤2}=p{X=0}+p{X=2}=0,12+0,08=0,2
Задача 6
Х номер учебного модуля в течении которого студенты успешно (без «допсы»)изучали математическую дисциплину. (Объём выборки n=50)
Пусть известна выборочная функция распределения.
,
F*(x)= ,,
,5
[ 5
1)Составить статистический ряд
2)Сколько студентов успешно сдали экзамен по математике во 2-ом и 3-ем модулях?
3)Построить полигон относительных частот
4)Вычислить следующие выборочные характеристики:mod; med; D*x; *x; S2; S.
5)Найти выборочное среднее и выборочную дисперсию для случайной величины У=5-4Х
Решение
1)Статистический ряд
Заметим, что n=50; ni=
xi |
1 |
2 |
3 |
4 |
5 |
|
|
0,1 |
0,16 |
0,2 |
|
0,34 |
0,2 |
|
5 |
8 |
10 |
17 |
10 |
|
2)Количество студентов успешно сдавших экзамен по математике во 2-ом и 3-
ем модулях определяем из таблицы: 8+10=18
Ответ 18 студентов.
Стр. 24
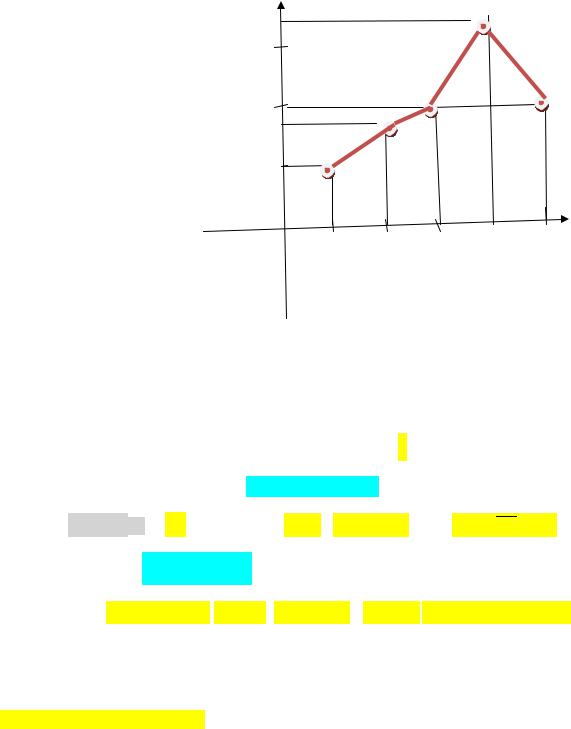
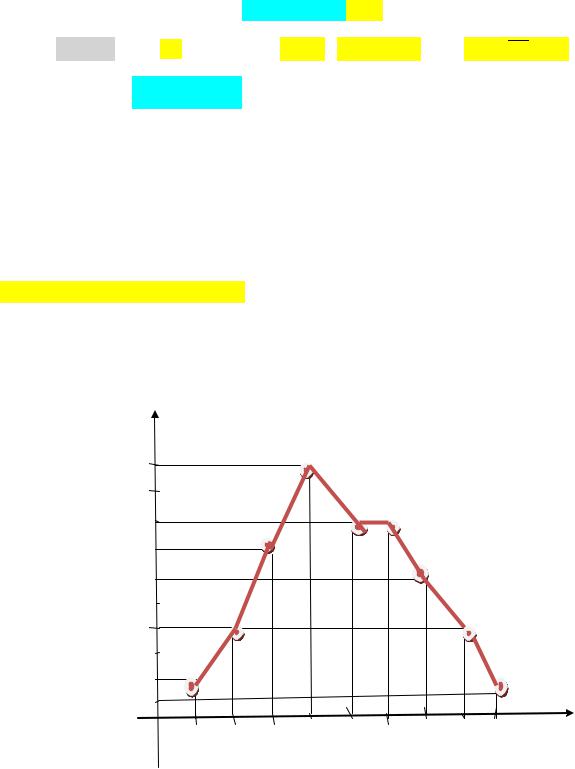
3)Полигон относительных частот
0,3
0,2
0,1
x
1 |
2 |
3 |
|
4 |
|
5 |
|
|
|
|
|
4)Выборочные характеристики
mod=4;med= |
|
= |
|
=4 |
|
|
|||
|
|
|
|
|
̅=∑



 =3,38
=3,38
Dx*=̅̅̅̅-(̅) ; ̅̅̅̅=∑ |
=12,98; Dx*=1.5556 |
*x=√ |
≈ , |
S2= *DX* S2= *12,98≈13,245; S≈3,64.
*DX* S2= *12,98≈13,245; S≈3,64.
Ответ: mod=4;med=3;̅ =3,38; Dx*=1.5556 ; *x≈ , S2≈13,245; S≈3,64.
5) Выборочное среднее и выборочная дисперсия для случайной величины У=5-4Х
̅=̅̅̅̅̅̅̅̅̅̅̅̅=5-4*̅=5-4*3,38= -8,52; D*Y=D*[5-4*X]=16*D*x=16*1,5556=24,8896.
Ответ:̅= -8,52; D*Y=24,8896
Задача 7.
Пусть Х генеральная совокупность (непрерывная случайная величина).
Стр. 25
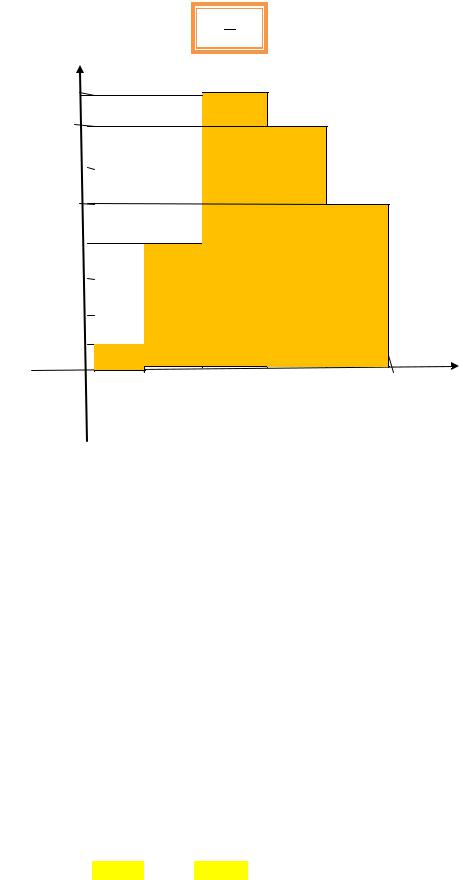
По выборке объёма n=50 построена гистограмма. |
|
||||
|
|
hi= ∆ |
|
|
|
f*(x) |
|
|
|
|
|
0.08 |
|
|
|
|
|
0,07 |
|
|
|
|
|
0,06 |
|
|
|
|
|
0,05 |
|
|
|
|
|
0,04 |
|
|
|
|
|
0,03 |
|
|
|
|
|
0,02 |
|
|
|
|
|
0,01 |
|
|
|
|
|
1 |
9 |
13 |
17 |
21 |
x |
5 |
|
||||
Найти: 1) статистический ряд;
2)сколько значений случайной величины Х попали в интервал(5;13) 3)полигон относительных частот
4)выборочную функцию распределения
5)выборочные числовые характеристики: ̅; D*X; *X; S2; S
6)выборочное среднее и выборочную дисперсию случайной величины
У=7-9*Х
Решение:
1)Статистический ряд
Найдём середины интервалов zi и относительные частоты и абсолютные частоты для каждого интервала: рi*=hi.∆ (∆=4); ni=pi*.n; n=50
Стр. 26
Zi |
3 |
7 |
11 |
15 |
19 |
|
hi |
0,01 |
0,04 |
0,08 |
|
0,07 |
0,05 |
|
0,04 |
0,16 |
0,32 |
0,28 |
0,2 |
|
ni |
2 |
8 |
16 |
|
14 |
10 |
2)Найдём число значений случайной величины Х, которые попали в интервал(5;13)
В этот интервал попадают два значения 7 и 11.
Сумма соответствующих абсолютных частот 8+16=24 ответ на данный вопрос.
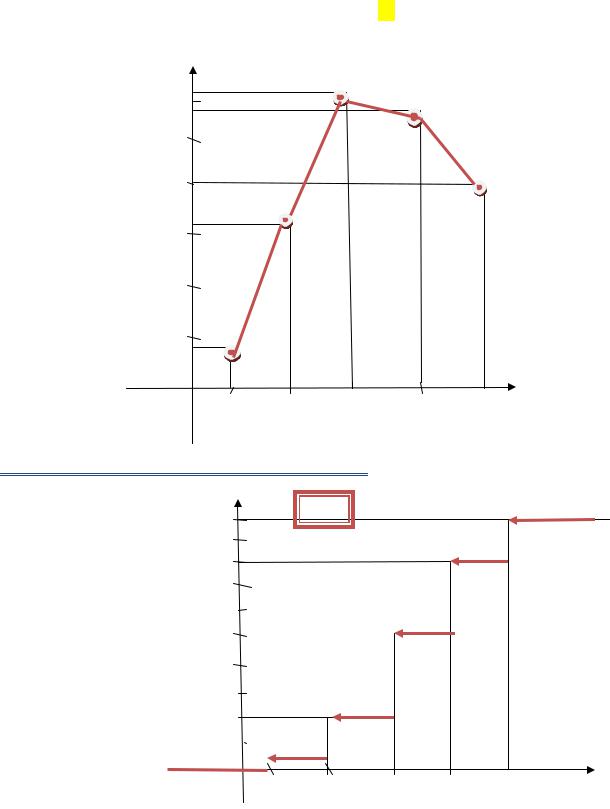
3)Полигон относительных частот
0,3
0,25
0,2
0,15
0,1
0,05
[
3 |
7 |
11 |
15 |
|
|
19 |
|||
|
||||
|
|
|
|
4)Выборочная функция распределения
|
|
1 |
F*(x) |
|
, |
7 |
|
|
|
||
F*(x)= , |
, |
5 |
|
, |
|
9 |
|
[ |
|
9 |
|
0,2
0,1
3 |
7 |
11 |
15 |
19 |
x |
|
|
|
|
|
Стр. 27 |
5)Выборочные числовые характеристики: ̅; D*X; *X; S2; S
̅=∑



 =12,76
=12,76
* |
= |
̅̅̅̅ |
- (̅) |
̅̅̅̅ |
∑ |
* |
=19,3024 |
* |
≈ . ; |
Dx |
|
|
= |
=182,12; Dx |
x=√ |
S2= *DX*S2= *19,3024≈19,696; S≈4,43.
*DX*S2= *19,3024≈19,696; S≈4,43.
Ответ: |
̅ |
=12,76; |
|
Dx*=19,3024 |
*x= |
√ |
|
|
≈ . S2≈19,696; S≈ ,43. |
|
|
|
|||||||
|
|
|
6)Выборочное среднее и выборочную дисперсию случайной величины У=7-9*Х
̅=̅̅̅̅̅̅̅̅̅̅̅̅=7-9*̅=7-9*12,76=-107,84; D*Y=D*[7-9*X]=81*D*x=1563,4944
Ответ:̅= -107,84; D*Y=1563,4944
Задача 8.
При выборочном обследовании 50 членов семей рабочих и служащих некоторого предприятия составлен полигон относительных частот.
0,20
0,18
0,16
0,14
0,12
0,10
0,08
0,06
0,04
0,02
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
x |
|
1)Составить статистический ряд
2)Сколько семей имеют более 5 членов в своей семье?
Стр. 28
3)Найти статистическую функцию распределения
4)Найти выборочные характеристики: mod;med; ̅; D*X; *x; S2; S.
5)Найти выборочное среднее и выборочную дисперсию случайной величины У=0,5-0,1*Х.
Решение:
1)Статистический ряд
Zi |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0,04 |
0,08 |
0,14 |
0,2 |
0,16 |
0,16 |
|
0,12 |
0,08 |
0,02 |
ni |
2 |
4 |
7 |
10 |
8 |
8 |
6 |
4 |
1 |
|
n=50;ni= . n
. n
2)Число семей, которые имеют более 5 членов семьи , соответствуют числам 6;7;8;9, сумма соответствующих частот: 8+6+4+1=19
Ответ 19
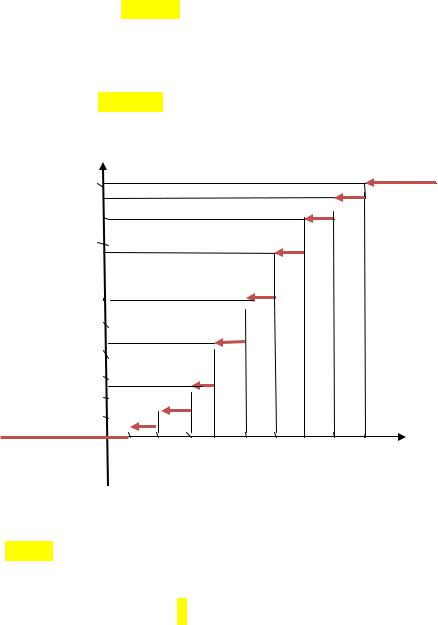
3)Статистическая функция распределения
|
|
, |
|
F*(x) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
, |
|
|
|
|
|
* |
|
, |
5 |
|
|
|
|
F |
(x)= |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
7 |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
9 |
|
|
|
|
|
|
[ |
9 |
|
|
|
|
0,1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
x |
4)Выборочные характеристики
Выборочная мода: mod=4 (на полигоне относительных частот это точка
максимума)
med= |
|
= |
|
=8 |
|
|
|||
|
|
|
|
|
Стр. 29

Выборочное среднее:̅= |
|
∑ |
(n=50) или ̅=∑ |
̅ |
=4,84 |
|
|||||
|
|
|
|
|
|
* |
̅̅̅̅ |
̅ |
̅̅̅̅ |
∑ |
* |
=3,7744 |
* |
≈ .94; |
|
Dx |
= |
-( |
); |
|
= |
=27,2; Dx |
x=√ |
||
S2= *DX* S2= *3,7744≈ ,8514; S≈ ,96.
*DX* S2= *3,7744≈ ,8514; S≈ ,96.
Ответ: mod=4; med=8; ̅=4,84; Dx*=3,7744; *x≈ .9 S2≈ ,8514; S≈ ,96
5)Выборочное среднее и выборочная дисперсия случайной величины У=0,5-0,1*Х
̅=̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅, , =0,5-0,1̅=0,5-0.1*4,84=0,016
D*Y=D*[0,5-0,1X]=0,01D*X=0,01*3,7744=0,037744
Отв т:̅=0,016; D*Y=0,037744
Стр. 30
