Пособие по математической статистике

Высшая школа экономики

теория вероятностей и математическая статистика

Анисимова Н.П. Ванина Е.А. Веретённик Е.

14

Оглавление

Глава 1 Описательная статистика

§1 Основные понятия и формулы.

§2 Решение типовых задач.

§3. Задачи для самостоятельного решения.

Глава 2. Точечное оценивание числовых характеристик и параметров распределения генеральной совокупности.

§1 Основные понятия и формулы.

§2 Решение типовых задач.

§3. Задачи для самостоятельного решения.

Глава 3.Интервальное оценивание числовых характеристик и параметров распределения генеральной совокупности.

§1 Основные понятия и формулы.

§2 Решение типовых задач.

§3. Задачи для самостоятельного решения....................................................................................

Глава 4. Проверка статистических гипотез. Критерий значимости.

§1 Основные понятия и формулы.

§2 Решение типовых задач .......................................................................................................

§3. Задачи для самостоятельного решения....................................................................................

Глава 5. Проверка гипотезы о законе распределения генеральной совокупности (критерий согласия).

§1 Основные понятия и формулы.................................................................................................

§2 Решение типовых задач .......................................................................................................

§3. Задачи для самостоятельного решения....................................................................................

Приложения

Стр. 2

Предисловие.

Настоящее пособие является продолжением «Практикум I» по дисциплине «Теория вероятностей и математическая статистика» для студентов факультета менеджмента, но может быть использовано и на других факультетах, где читается аналогичный курс. Цель данного пособия состоит в освещении возможностей практического применения методов теории вероятностей и математической статистики, освоении методики решения типовых задач.

Отличительной особенностью данного пособия являются краткий обзор основных теоретических понятий и формул. В сборнике подробно разбирается решение типовых задач, а все задачи для самостоятельного решения снабжены указаниями и ответами.

При успешном выполнении домашних заданий студенты гарантировано будут подготовлены к итоговому экзаменационному тесту.

Данное пособие поможет и преподавателям, ведущим этот курс.

Авторы надеются, что данное пособие будет активно использовано в учебном процессе, а также будут благодарны, если в пособии будут отмечены опечатки или ошибки.

Стр. 3

Глава 1. Описательная статистика.

§1Основные понятия и формулы.

Генеральная совокупность. Выборка. Выбор.

Определение. Генеральной совокупностью называется множество возможных

значений изучаемой случайной величины Х с приписанным этому множеству законом распределения F(x).

Числа, составляющие генеральную совокупность, называются её элементами. Закон распределения F(x) называется генеральным законом распределения, а числовые характеристики случайной величины Х называются генеральными характеристиками.

Выборкой называется множество измеренных значений x1;x2;…;xn случайной величины Х.

Пусть проводится серия из «n» опытов. Наблюдающиеся значения хi случайной величины Х называют так же вариантами.

Результаты опытов занесём в таблицу.

Выборочной совокупностью или случайной выборкой называют

«n» мерную случайную величину Y=(X1;X2;…;Xn)

Выборка объёма «n» -это значение выборочной совокупности или «n»-мерная точка y=(x1;x2;…;xn)

Стр. 4

Замети, что ( )варианта в «j» серии в «i»опыте.

Xiслучайная величина (значение генеральной совокупности Х в «i» опыте в серии испытаний).

Это важно!

Компоненты выборочной совокупности X1;X2;..;Xn

1)независимые в совокупности случайные величины; 2)имеют такое же распределение , как генеральная совокупность Х;

Процесс составления выборки называется выбором.

Простым случайным выбором называется выбор, удовлетворяющий следующим требованиям:

1. Выбор является случайным.

Случайный выбор объективен, гарантирует от пропуска скрытых закономерностей в генеральной совокупности.

2.Каждый элемент генеральной совокупности может быть выбран.

3.Каждый элемент выбирается независимо от остальных.

4.Все элементы выборки получаются в равных условиях.

Это свойство можно выразить, введя случайную величину , принимающую выборочные значения x1;x2;…;xn с одной и той же вероятностью .

Дискретное равномерное распределение с законом , заданным формулой P{X*=xk}= , k=1;2;…;n называется выборочным

распределением, а его числовые характеристики выборочными числовыми характеристиками.

В реальных условиях простой случайный выбор не всегда осуществим

Виды реальных выборов.

1.Механический выбор. В этом случае элементы генеральной совокупности выбираются по какой-либо закономерности. Например, измерения производятся через равные промежутки времени, контролируется каждая десятая деталь, сходящая с

Стр. 5

конвейера, каждый пятый человек по списку. Применяется для автоматизированного контроля.

2.Серийный выбор. Элементы в этом случае выбираются не по одному, а сериями. Например, контролю подвергается не одна таблетка лекарства, а упаковка, не один человек из какой-либо группы, а вся группа. Диктуется условиями производства и обследования.

3.Типический выбор. В этом случае генеральная совокупность делится на непересекающиеся части. Из каждой части выбираются элементы в количестве, пропорциональном объёму каждой части. Так можно получить сведения о средней зарплате в отрасли, об урожайности поля, о политических предпочтениях людей. Характерен для экономических и социологических исследований.

4.Субъективный выбор на основе какого-либо субъективного принципа. Например, домашнее задание проверяется не у всех студентов, а только у тех , которые не вызывают доверия у преподавателя.

5.Выбор с помощью случайных независимых измерений (температура среды, величина тока, загрязнённость реки). Характерен для инженерных и естественнонаучных исследований.

Все типы выборов могут комбинироваться между собой.

В математической статистике рассматривается только простой случайный выбор.

К выборкам, как и к выбору, предъявляется ряд требований.

Важнейшим из них является требования: 1) репрезентативности (представительности). Это требование означает, что выборка должна хорошо представлять всю генеральную совокупность.

2)однородности выборки. Это означает, что условия проведения экспериментов для получения выборки не должны меняться.

Будем различать малые и большие выборки, так как они отличаются методами обработки. Для обработки большой выборки привлекаются асимптотические методы, основанные на центральной предельной теореме. В статистической

практике принято считать выборку с объёмом n>30 большой.

Вариационный и статистические ряды.

Выборка является труднообозримым множеством. Для дальнейшего изучения выборку подвергают перегруппировке.

Стр. 6

Определение1. Вариационным рядом называется последовательность всех элементов выборки, расположенных в неубывающем порядке. Одинаковые элементы повторяются.

Запись вариационного ряда: х(1);х(2);…;х(n); xmin=x(1); xmax=x(n)

Разность между максимальным и минимальным элементами называется размахом или широтой выборки: R=xmax-xmin

Определение 2. Средний элемент вариационного ряда, если «n» нечётное, или полусумма двух средних элементов , если «n» чётное, называется медианой выборки и обозначается med:

( )

med=[ ( ) ( )

Определение 3. Элементы вариационного ряда, на четверть отстоящие от краёв, называются соответственно нижней и верхней квартилями и обозначаются и .

Математически точно квартили определяются по формулам:

наибольшее целое число, не превосходящее а)

.=x(n-i+1)

Числа xmin;; med;; xmax дают сжатую информацию о выборке и,

следовательно, о генеральной совокупности.

Они могут быть изображены в виде так называемого ящика с усами.

Xmax

xmin

Стр. 7

Определение4. Статистическим рядом называется последовательность различных элементов zi вариационного ряда

(z1 z2 .. zk) с указанием частот ni повторения элементов.

n1+n2+…+nk=n

Рассмотрим относительную частоту для значения zi: pi*=.

Если рассмотреть некоторую фиктивную случайную дискретную случайную величину Х* , которая задаётся рядом распределения:

Определение 5. Полигон частот (относительных частот) это ломаная с вершинами в точках (zi;ni) или (zi; )

Если плотность распределения генеральной совокупности Х является достаточно гладкой функцией, то полигон относительных частот является достаточно хорошим приближением функции плотности f(x)

Определение 6.Выборочная мода это наиболее часто встречающийся элемент статистического ряда, который обозначается mod.

(Обычно сначала изучают спрос и выявляется мода наиболее часто встречающаяся варианта)

Стр. 8

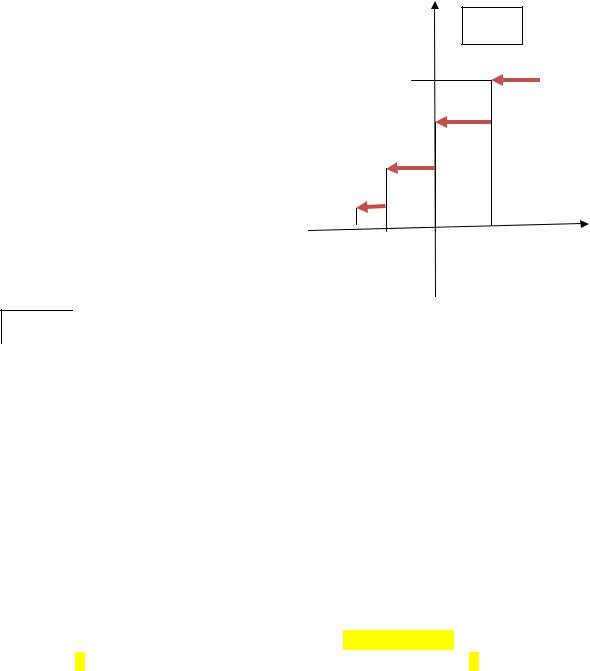
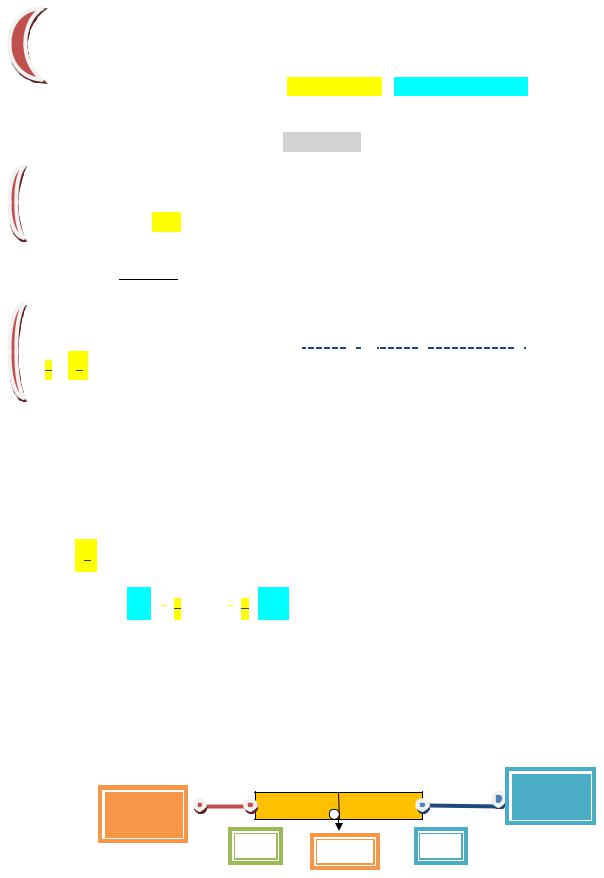
Определение 7. Выборочной (эмпирической) функцией распределения называется относительная частота события Х х, полученная по выборке.

F(x)

F*(x)=

[

Группированный статистический ряд. Гистограмма.

Если выборка получена из непрерывной генеральной совокупности и объём её большой, то вариационный и статистические ряды, как и сама выборка, будут трудно обозримыми множествами. Действительно, в этом случае при достаточно точном измерении практически не будет равных элементов выборки, ибо вероятность равенства значений непрерывной случайной величины равна нулю. Тогда прибегают к другому способу группирования выборки.

1.Промежуток [xmin;xmax] делится на некоторое число «к» равных по длине промежутков. Обозначим эти промежутки слева направо через ∆1;∆2;…;∆к. Если точки, разделяющие промежутки , обозначить а0;а1;…;ак, то ∆1=[xmin;a1];

∆2=[a1;a2];…;∆i=[ai-1;ai];…;∆k=[ak-1;xmax]. Здесь а0=xmin; ak=xmax.

2.Пусть ni число элементов выборки, попавших в промежуток ∆i. Числа n1;n2;…;nk называются частотами попадания элементов выборки в рассматриваемые промежутки.

Примечание

Для определения «к» можно рекомендовать полуэмпирическую формулу

Стр. 9

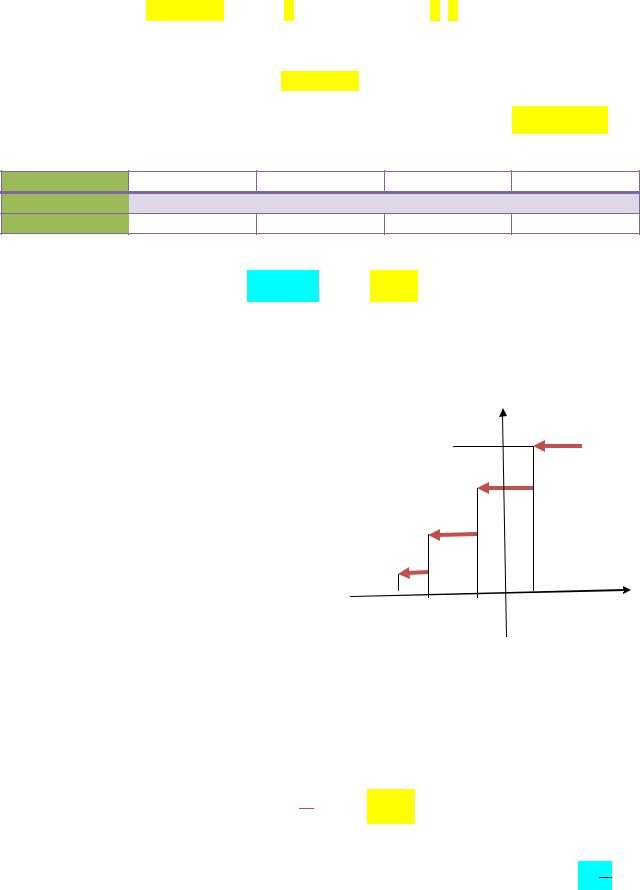
к=1,72*n1/3 (Здесь nобъём выборки; 30≤n≤1000)

Применяется также формула Старджесса

к=1+3,3lgn

3.Длина промежутков ∆1;∆2;…;∆к определяется по формуле: ∆==

4.Составляем статистический ряд для группированной выборки:

Здесь ziсередина промежутка ∆i

zi= pi*=.

4.Выборочная (эмпирическая) функция распределения

F*(x)=

[

x

5.Гистограмма выборки

Определение: Гистограмма выборки это кусочно-постоянная функция

( ) = ∆ x ∆I (pi*=.)

(В некоторых случаях, гистограммой выборки называют так же ступенчатую

фигуру, образованную прямоугольниками с основаниями ∆i и высотами hi= ∆ )

Заметим, что площадь ступенчатой фигуры равна 1.

Стр. 10