
Пособие по математической статистике
.pdf
Задача 18
Известно, что заработная плата некоторого работника подчиняется закону распределения Парето. Минимальная заработная плата составляет 4 тысячи рублей. Для определения попадания заработной платы в интервал от 4 до 12 тысяч была составлена статистическая таблица, по которой найдена точечная оценка параметра распределения*=1,76. Необходимо проверить выполнение гипотезы  на уровне значимости =0,05:
на уровне значимости =0,05:
Х – заработная плата подчиняется закону Парето.
(Ответ: гипотезу 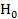 отвергаем на данном уровне значимости).
отвергаем на данном уровне значимости).
xi |
4 |
7 |
9 |
12 |
16 |
|
|
|
|
|
|
ni |
6 |
3 |
4 |
2 |
5 |
|
|
|
|
|
|
Задача 19
Наблюдалось следующее распределение по минутам числа появлений охранника в дверях ювелирного магазина, имеющего по должностной инструкции 6-минутный интервал
появления. Проверить гипотезу о равномерном распределении на основании данной выборки, уровень значимости =0,05.
|
|
|
|
|
|
|
1/6 |
f(x) |
|||
|
|
|
|
|
|
|
|
|
|||
|
1 |
, x (0;6) |
|
|
|
|
|||||
f (x) |
|
|
|
|
6 |
||||||
|
|
|
|
|
|||||||
6 |
|
|
|
|
|
|
|
||||
: |
0, x (0;6) |
|
|
F(x) |
|||||||
0, x |
0 |
1 |
|||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
F (x) |
|
x |
,0 |
x 6 |
|
|
|
|
|||
|
|
|
6 |
||||||||
|
|
|
|
||||||||
6 |
|
|
|||||||||
|
1, x 6 |
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
Интервал в минутах |
|
ni |
|
|
|
|
|||||
[0;1) |
|
|
|
|
|
28 |
|
|
|
|
|
[1;2) |
|
|
|
|
|
25 |
|
|
|
|
|
[2;3) |
|
|
|
|
|
30 |
|
|
|
|
|
[3;4) |
|
|
|
|
|
29 |
|
|
|
|
|
[4;5) |
|
|
|
|
|
32 |
|
|
|
|
|
[5;6) |
|
|
|
|
|
26 |
|
|
|
|
|
(Ответ: нет оснований отвергнуть гипотезу 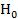 ).
).
Задача 20
Время обслуживания продавцом покупателя в бакалейной лавке – это случайная величина Х. Выдвигается гипотеза 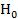 : Х exp(а) . Для нахождения точечной оценки
: Х exp(а) . Для нахождения точечной оценки
параметра была составлена группированная выборка ( ni - число продавцов). N=30.
Стр. 161

№Границы zi - середины ni интервалов интервалов
1 |
[0;0,5) |
0,25 |
8 |
|
|
|
|
2 |
[0,5;1) |
0,75 |
8 |
|
|
|
|
3 |
[1;1,5) |
1,25 |
6 |
|
|
|
|
4 |
[1,5;2) |
1,75 |
4 |
|
|
|
|
5 |
[2;2,5) |
2,25 |
3 |
|
|
|
|
6 |
[2,5;3) |
2,75 |
1 |
|
|
|
|
Используйте метод моментов для нахождения точечной оценки . Затем проверьте
гипотезу 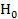 о показательном распределении СВ Х при доверительной вероятности
о показательном распределении СВ Х при доверительной вероятности
=0,05
|
|
(Ответ: а* 0,93 , нет оснований отвергнуть гипотезу |
|
). |
|
|
|
|||||||||||||
|
|
|
|
|
|
Задача 21 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
и 2 . |
||||||||
|
Х имеет распределение, заданное таблицей. Неизвестные параметры 1 |
|||||||||||||||||||
Точечные оценки: * 0,14 |
|
* 0,2 (n=24). |
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
хi |
|
-2 |
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
|
2 2 1 |
|
|
0,2 |
|
|
|
|
|
|
4 1 |
|
3 |
|
|
|
1 5 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,25 |
|
|
0,2 |
|
|
|
|
|
|
0,3 |
|
|
|
|
0,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ni |
|
|
6 |
|
|
5 |
|
|
|
|
|
|
7 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
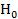 : Х – имеет данное распределение. Проверить данную гипотезу на уровне значимости =0,1, используя критерий согласия 2 Пирсона
: Х – имеет данное распределение. Проверить данную гипотезу на уровне значимости =0,1, используя критерий согласия 2 Пирсона
(Ответ: нет оснований отвергнуть гипотезу 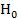 ).
).
Задача 22
В мешке 60 шаров трех цветов (синий/белый/красный). Фокусник может вытащить только 1 шар. Можно ли утверждать, что фокусник с равной вероятностью вытащит шар любого цвета, т.е. необходимо проверить гипотезу 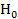 : СВ Х (тип шара) – распределена по дискретному равномерному закону на уровне значимости =0,1 (Ответ: гипотезу
: СВ Х (тип шара) – распределена по дискретному равномерному закону на уровне значимости =0,1 (Ответ: гипотезу
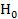 принимаем на данном уровне значимости).
принимаем на данном уровне значимости).
№ |
хi |
pi |
ni |
|
|
|
|
1 |
Белый шар |
1/3 |
24 |
|
|
|
|
2 |
Синий шар |
1/3 |
15 |
|
|
|
|
3 |
Красный шар |
1/3 |
21 |
|
|
|
|
Стр. 162

Задача 23
Время ожидания своей очереди на подключение к Интернету – это СВ Х. В течение нескольких месяцев работники компании, предоставляющей услуги по подключению, составляли статистику по клиентам. Была составлена следующая группированная выборка:
№ |
Границы |
zi - середины |
ni |
|
|
интервалов |
интервалов |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
[0;0;1) |
0,05 |
18 |
|
|
|
|
|
|
2 |
[0;1;0;2) |
0,15 |
10 |
|
|
|
|
|
|
3 |
[0;2;0;3) |
0.25 |
8 |
|
|
|
|
|
|
|
|
|
|
|
4 |
[0;3;0;4) |
0,35 |
6 |
|
|
|
|
|
|
5 |
[0;4;0;5] |
0,45 |
4 |
|
|
|
|
|
|
7 |
[0;5;0;6) |
0,55 |
2 |
|
|
|
|
|
|
|
|
|
|
|
8 |
[0;6;0;7] |
0,65 |
2 |
|
|
|
|
|
|
Выдвигается гипотеза:  : Х Ехр(а).
: Х Ехр(а).
Т.к. параметр неизвестен, то необходимо найти его точечную оценку по методу моментов, а затем проверить выполнение гипотезы на уровне значимости =0,05
(Ответ: а*=4,67, гипотезу  принимаем).
принимаем).
Задача 24
Комиссия по проверке качества на заводе по сборке швейных машинок должна проверить 50 машинок. Х – число возможных неисправностей а одной швейной машинке имеет распределение Пуассона с неизвестным параметром . После проверки была составлена сводная статистическая таблица ( xi - количество неисправностей в одной
машинке). |
P{X k} |
k |
|
|
|
|
|
|
|
|
|
|
|||||
e , для n=50. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
||
|
xi |
|
0 |
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
|
|
|
ni |
|
12 |
|
15 |
|
10 |
|
7 |
|
|
4 |
|
2 |
|
|
|
|
pi |
|
е |
|
* е |
|
2 е |
|
3 |
е |
4 |
е |
5 |
е |
|
||
|
|
|
|
|
|
|
|
2! |
|
3! |
|
|
4! |
|
5! |
|
|
Была получена точечная оценка параметра : |
при n=50 (неизвестен один параметр, т.е. |
||||||||||||||||
l=1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
: на уровне значимости =0,05 проверить гипотезу о том, что Х – имеет |
|||||||||||||||
распределение Пуассона. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(Ответ: нет оснований отвергнуть гипотезу |
). |
|
|
|
|
|
|
||||||||
Стр. 163

Краткий обзор.
Определение. Генеральной совокупностью называется множество возможных значений изучаемой случайной величины Х с приписанным этому множеству законом распределения F(x).
Числа, составляющие генеральную совокупность, называются её элементами. Закон распределения F(x) называется генеральным законом распределения, а числовые характеристики случайной величины Х называются генеральными характеристиками.
Выборкой называется множество измеренных значений x1;x2;…;xn случайной величины Х.
Пусть проводится серия из «n» опытов. Наблюдающиеся значения хi случайной величины Х называют так же вариантами.
Выборочной совокупностью или случайной выборкой называют
«n» мерную случайную величину Y=(X1;X2;…;Xn)
Выборка объёма «n» -это значение выборочной совокупности или «n»-мерная точка y=(x1;x2;…;xn)
Определение1. Вариационным рядом называется последовательность всех элементов выборки, расположенных в неубывающем порядке. Одинаковые элементы повторяются.
Запись вариационного ряда: х(1);х(2);…;х(n); xmin=x(1); xmax=x(n)
Разность между максимальным и минимальным элементами называется размахом или широтой выборки: R=xmax-xmin
Определение 2. Средний элемент вариационного ряда, если «n» нечётное, или полусумма двух средних элементов , если «n» чётное, называется медианой выборки
и обозначается med:
( )
med=[ ( ) ( )
Определение3 Статистическим рядом называется последовательность различных элементов zi вариационного ряда
(z1 z2 .. zk) с указанием частот ni повторения элементов.
Стр. 164
n1+n2+…+nk=n
удобно называть такой ряд статистическим рядом.
Заметим, что |
∑ |
=1 |
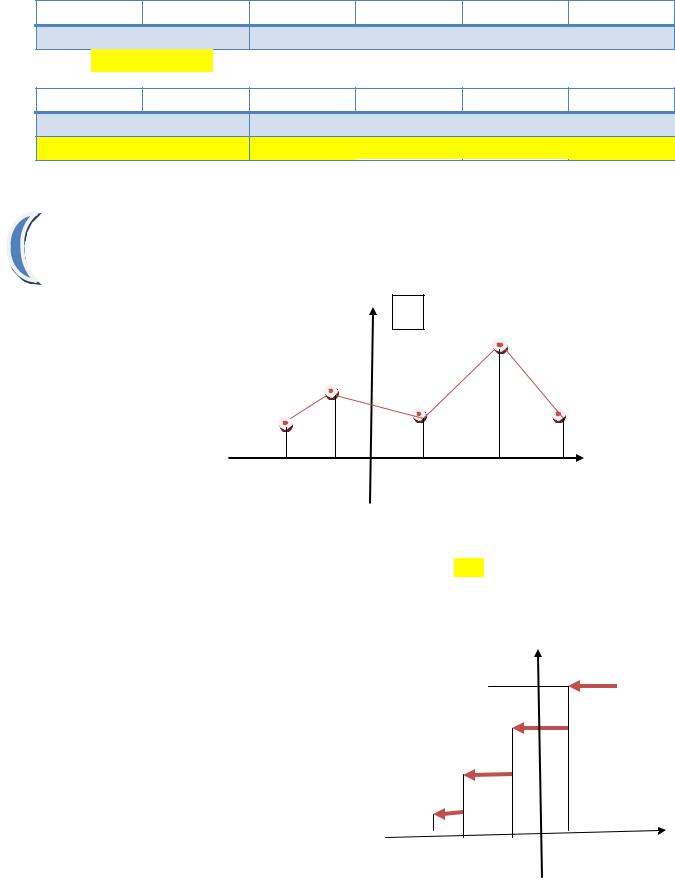
Определение 4. Полигон частот (относительных частот) это ломаная с вершинами в точках (zi;ni) или (zi; )
z1 |
zi |
mod |
zk |
x |
|
|
|
|
|
|
|
|
|
|
Определение 5. Выборочная мода это наиболее часто встречающийся
элемент статистического ряда, который обозначается mod.
Выборочная (эмпирическая) функция распределения
F*(x)=P{X* x}=∑ |
= |
|
∑ |
|
|
||||
|
|
|
|
1 |
F*(x)=
[
x
.Гистограмма выборки
Стр. 165

Определение: Гистограмма выборки это кусочно-постоянная функция
( ) = ∆ x ∆I (pi*= .)
.)
Определение: Статистикой называется любая функция выборочной совокупности, которая является случайной величиной.
Определение: Точечной статистической оценкой неизвестной числовой характеристики или параметра распределения называется функция выборочной
совокупности
̃= ( X1;X2:…;Xn); значение этой случайной величины для конкретной выборки
*= (х1;x2;…;xn) принимается за приближённое значение параметра .( *≈)
Критерии качества точечных оценок.
Состоятельность
Оценка ̃n=̃n(X1;X2;…;Xn) называется состоятельной оценкой , если она стремится
p
по вероятности к с ростом n: ̃n . Это означает, что для любого >0 n ∞
выполняется соотношение |
|
̃ |
|
) |
|
( |
|||
|
|
|
|
Несмещённость
Оценка n называется несмещённой оценкой параметра , если математическое
ожидание оценки равно : M[̃n]=
В противном случае оценка называется смещённой.
Разность =M[̃n]- называется смещением оценки.
>0 смещение вправо
0 с щ в в
Для несмещённых оценок систематическая ошибка равна нулю ( =0)
Эффективность
Оценка ̃n*числовой характеристики или параметра распределения
называется эффективной в рассматриваемом классе Т состоятельных и несмещённых оценок, если она имеет в этом классе минимальную дисперсию.
D̃n*=minD̃n
T
Стр. 166
Из двух оценок ̃1n |
и ̃2n |
одной и той же числовой характеристики или параметра |
|||||||||
распределения в классе Т состоятельных и несмещённых оценок более |
|
||||||||||
эффективной считается та, дисперсия которой меньше. |
|
||||||||||
Если имеет место неравенство: |
D̃1n D̃2n ,то оценка ̃1n более эффективная |
||||||||||
|
|
оценка , чем оценка ̃2n. |
|
|
|
|
|
||||
Отношение D̃1n |
/D̃2n |
называется относительной эффективностью оценки ̃2n |
|||||||||
|
|
относительно оценки ̃1n |
|
|
|
|
|
||||
Краткий обзор основных точечных оценок для генерального математического |
|||||||||||
|
|
ожидания и дисперсии. |
|
|
|
|
|
||||
Генеральное |
Точечная оценка |
|
Свойства |
|
|
При n>30 |
|
||||
математическое |
статистика |
|
|
1)состоятельная |
|
|
|||||
|
|
|
асимптотически |
||||||||
ожидание |
|
̅= ∑ |
|
|
оценка |
|
|
||||
|
|
|
|
|
приближается к |
||||||
M[X]=m |
|
|
|
̅ m |
|
|
|||||
Выборочное |
|
|
|
нормальному |
|||||||
|
|
|
n ∞ |
|
|
||||||
|
|
|
|
|
распределению |
||||||
|
|
среднее |
|
|
2)несмещённая |
|
|||||
|
|
|
|
|
̅ N(m; /√ |
|
|||||
|
|
|
|
|
|
) |
|||||
|
|
|
|
|
оценка |
|
|
||||
|
|
|
|
|
|
|
|
2=D[X] |
|
||
|
|
|
|
|
M[̅ =m |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Генеральная дисперсия |
Точечная оценка |
|
|
|
Свойства |
|
|||||
D[X]= 2 |
|
Статистика |
|
1)состоятельная оценка |
|||||||
|
|
̃X= |
∑ |
( |
̅) |
|
|
|
̃X D[X] |
|
|
|
|
Выборочная дисперсия |
|
|
n ∞ |
|
|||||
|
|
2)смещённая оценка |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
M[̃X]= D[X] |
|
||
|
|
|
|
|
|
|
величина смещения |
||||
|
|
|
|
|
|
|
|
|
= - |
|
|
|
|
Точечная оценка |
|
|
|
Свойства |
|
||||
|
|
Статистика |
|
1)состоятельная оценка |
|||||||
|
|
̃= |
∑ |
( |
̅) |
|
|
|
̃ D[X] |
|
|
|
|
Исправленная дисперсия |
|
|
n ∞ |
|
|||||
|
|
2)несмещённая оценка |
|||||||||
|
|
|
̃= |
|
̃X |
|
|||||
|
|
|
|
|
|
|
M[̃]=D[X] |
|
|||
|
|
Точечная оценка |
|
|
|
Свойства |
|
||||
|
|
Статистика |
|
1)состоятельная оценка |
|||||||
|
|
̃ = |
∑ |
( |
) ; |
|
|
|
̃ D[X] |
|
|
|
|
Центрированная |
|
|
|
n ∞ |
|
||||
|
|
|
дисперсия |
|
2) |
с |
щё |
ая |
ка |
||
|
|
|
|
|
|
|
|
M[̃ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Стр. 167 |
|
Свойства выборочного среднего
|
1 |
|
|
|
|
|
|
|
̅=С |
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
̅̅̅̅̅̅̅̅ |
|
̅ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
к |
с=к +с |
|
|
|
|
|
||||||
|
3 |
|
|
|
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅ |
=к |
̅ |
к |
̅ |
||||||||||
|
|
|
|
к |
|
|
|
к |
|
|
|
|
|
||||||
|
4 |
|
|
|
Y= (X) |
̅= |
|
|
∑ |
|
( ) |
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
N |
|
Выборочная дисперсия |
|
|
|
Выборочное среднее квадратичное |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отклонение |
|
||||
1 |
|
|
|
|
D*[C]=0 |
|
|
|
|
|
|
|
|
|
*[C]=0 |
|
|||
2 |
|
D*[kX+C]=k2D*[X] |
|
|
|
|
|
|
|
*[kX+C]= k *[X] |
|||||||||
3 |
|
Х и У независимые случайные |
|
|
Х и У независимые случайные величины |
|
|||||||||||||
|
|
|
|
|
величины |
|
|
|
*[k1X+k2Y+C]=√ |
|
|
|
|||||||
|
|
D*[k1X+k2Y+C]= D*[X]+ D*[Y] |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
К атк й |
з |
т ч ч ы |
|
к а а |
т |
в |
я |
с |
в ы |
ас |
й. |
|
Название |
|
Определение |
|
|
|
|
|
Точечные оценки |
||||
|
|
|
|
|
|
|
|
|
|
параметров |
||
Биномиальное |
|
Х число появлений события А |
|
̃= ̅ |
точечная |
|||||||
(оценивается |
в «m» испытаниях |
|
Х {0;1;2;…;m} |
|
|
оценка параметра Р |
||||||
параметр |
|
Имеем выборку объёма «n»: |
|
|
||||||||
|
|
|
|
|
P*= ̅≈p |
|||||||
р=р(А)) |
|
(X1;X2;…;Xn); Хi {0;1;2;…;m} |
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
|
|
P{X=Xi}= |
* |
*( |
|
|
) |
|
|
|
|
|
Распределение |
|
Имеем выборку объёма «n»: |
|
|
̃ |
̅ точечная |
||||||
|
|
|
|
|||||||||
Пуассона |
|
(X1;X2;…;Xn); Хi {0;1;2;…} |
|
|
оценка параметра |
|||||||
(Оценивается |
|
P{X=Xi}= |
*е- |
|
|
|
|
|
*=̅≈ |
|||
параметр ) |
|
|
|
|
|
|
|
|
|
|
|
|
Геометрическое |
Имеем выборку объёма «n»: |
|
|
|
|
̃ |
̅ |
|
||
распределение |
(X1;X2;…;Xn); Хi {1;2;…} |
|
|
точечная оценка |
|
|||||
(оценивается |
P{X=Xi}=( |
) |
* p |
|
|
параметра Р |
|
|||
параметр |
|
|
|
|
|
|
|
* |
=̅≈р |
|
р=р(А)) |
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
Равномерное |
f(x)=[ |
|
|
{ |
̃ |
̅ |
|
√ |
̃ |
|
распределение |
|
̃ |
̅ |
|
√ |
̃ |
|
|||
на отрезке |
̅ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
̅ |
√ |
|
|
X R[a;b] |
|
|
|
|
|
|
{ |
; |
||
1/b-a |
|
|
|
|
|
̅ |
√ |
|||
(оцениваются |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
*=√ |
|
|
||
параметры |
|
|
|
|
|
|
|
|
||
a |
|
|
|
|
|
|
|
|
|
|
а и b) |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Стр. 168
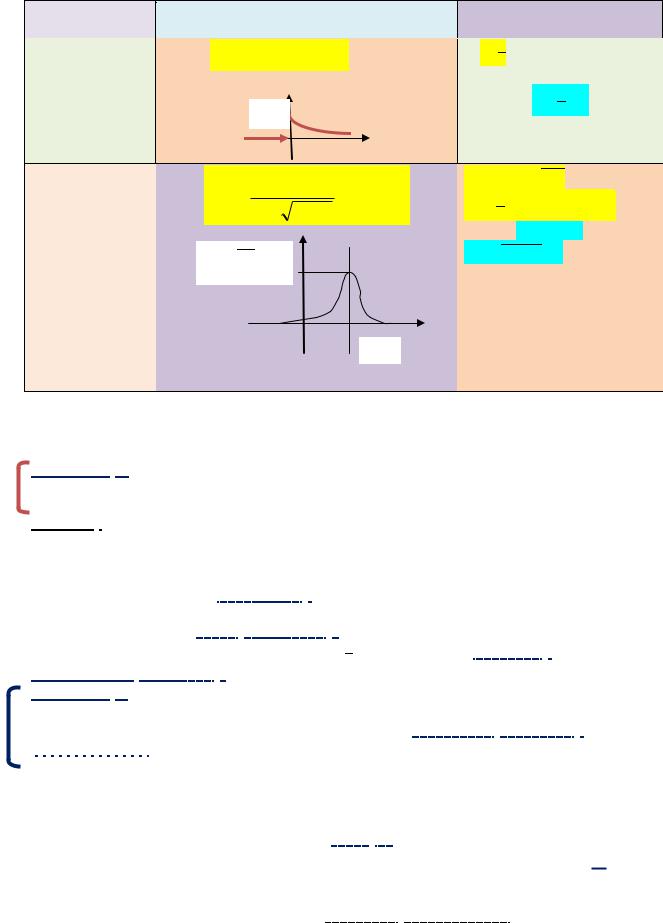
Показательное |
f(x)=[ |
|
|
|
|
̃=̅ точечная оценка |
||||
распределение |
|
|
|
|
||||||
|
|
|
|
|
|
параметра «а» |
||||
Х ехр(а) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
а*=̅≈а |
|
||
(оценивается |
a |
|
|
|
|
|
|
|
||
параметр «а») |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормальное |
|
|
|
( x m)2 |
|
̅ |
̃= |
√̃ |
; |
|
распределение |
|
1 |
e |
2 2 |
m= ; |
|
|
|||
fx(x)= |
̃X= |
∑ |
( |
|
̅) |
|||||
X N(m; ) |
2 |
|
|
|
||||||
(оцениваются |
|
|
|
|
|
|
m*=̅≈m; |
|
||
Параметры |
1/σ√ |
|
|
|
* |
=√ |
|
≈ |
|
|
m и ) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
m
Интервальные оценки.
Опрелеление.1. Если выполняется соотношение : p{ 1< < 2}= , то интервал
( 1; 2)называется доверительным интервалом., который покрывает неизвестную
генеральную характеристику с доверительной вероятностью . Замечание. 1= 1(х1;х2; .;xn) и 2= 2(х1;х2; .;xn)—известные функции выборочной
совокупности, т.е. статистики. В данной выборке это числовые значения.
Статистики 1 и 2 являются точечными оценками . Одна даёт левую, а другая —правую границы, между которыми содержится с вероятностью .
Число называется также надёжностью, с которой доверительный интервал накрывает
.
Число =1- называется уровнем значимости.
Половину длины доверительного интервала = ( 2- 1) называют точностью
доверительного оценивания.
Определение 2.Пусть известна одна точечная оценка ̂ генеральной числовой характеристики или параметра распределения .
Если выполняется соотношение: P{| -̂|< }= , то число называется точностью, а число—надёжностью оценки ̂ генеральной числовой характеристики .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К атк й з |
т ва ь ы |
к а а т в я с в ы ас |
й. |
|||||||
Задача 1
(Доверительный интервал для математического ожидания при известном )
Дано:
o Генеральная совокупность X имеет нормальное распределение, причем известна:
N (m, )
Стр. 169

o (X1, X2 , X3 ,.., Xu ) - выборка
|
По доверительной вероятности |
построить доверительный интервал для |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
математического ожидания |
P{m ( 1; 2 )} 1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
U |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ответ: P{m (X |
; X )} 1 |
; |
|
n |
|
|
1 2 |
|
; где |
1 |
2 |
- квантиль порядка |
|
2 , |
||||
Задача 2
(Построение доверительного интервала для математического ожидания при неизвестном σ)
Дано:
X 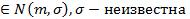 ;
;
По доверительной вероятности построить доверительный интервал для математического ожидания P{m ( 1; 2 )} 1
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
(k) |
|
|
t |
|
(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
||
|
Ответ: |
P{m (X ; X )} 1 , где |
|
2 |
S |
; где |
2 |
- квантиль |
||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
порядка |
2 ; распределение Стьюдента с k степенями свободы; k=n-1; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
̂ √̂; ̂= |
|
|
∑ ( |
̅) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Задача 3
(Построение доверительного интервала σ2 при известном параметре m) Дано:
o X N(m, )
o |
m (математическое ожидание)- известно; |
|
|
|
|
|
|
||||||||||||||||||||
o |
( X1, X 2 , X u ,...) |
- выборка; |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
o |
– уровень значимости. |
|
|
|
|
|
|
|
|
||||||||||||||||||
Найти: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
o |
доверительный интервал для 2 ( и для ): |
P{ 2 ( 1, 2 )} 1 |
|||||||||||||||||||||||||
P{ ( 1, 2 )} 1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
доверительный |
|
интервал |
|
|
для |
2 ( ): |
|||||
|
P{ 2 ( |
|
nS02 |
|
, |
|
|
nS02 |
)} 1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(n) |
|
(n) |
|
|
|
1 n |
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
S02 |
|
( X i |
m)2 |
|
(n) |
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
; |
n i 1 |
|
; где |
|
2 |
|
– квантиль |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
P{ ( |
|
|
|
nS0 |
|
|
, |
|
nS0 |
)} 1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
(n) |
|
|
|
2 (n) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
|||||
|
порядка |
2 |
распределения 2 с n степенями свободы; |
1 |
2 |
– квантиль |
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
порядка |
|
2 |
распределения 2 с n степенями свободы |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стр. 170 |
|
