
Пособие по математической статистике
.pdf
Правило принятия решения : Если zвыб (zкр1 ; zкр 2 ) , то гипотезу Но
на уровне значимости принимаем на уровне значимости . Если zвыб (zкр1 ; zкр 2 ) , то гипотезу Но отвергаем в пользу
альтернативной.
В общем случае: если Zвыб Vкр , то гипотеза Но отвергается, так как в
результате одного лишь испытания, получения выборки произошло практически невозможное событие: Zвыб Vкр с вероятностью . Если Zвыб
(V \ Vкр ), то гипотеза Но принимается.
Ошибки первого (I) и второго (II) рода
Суждения о принятии или отвержении выдвинутой статистической гипотезы не являются абсолютными, а носят лишь вероятностный характер, т.е. являются правдоподобными. Принимая или отвергая гипотезу, мы можем совершить ошибку.
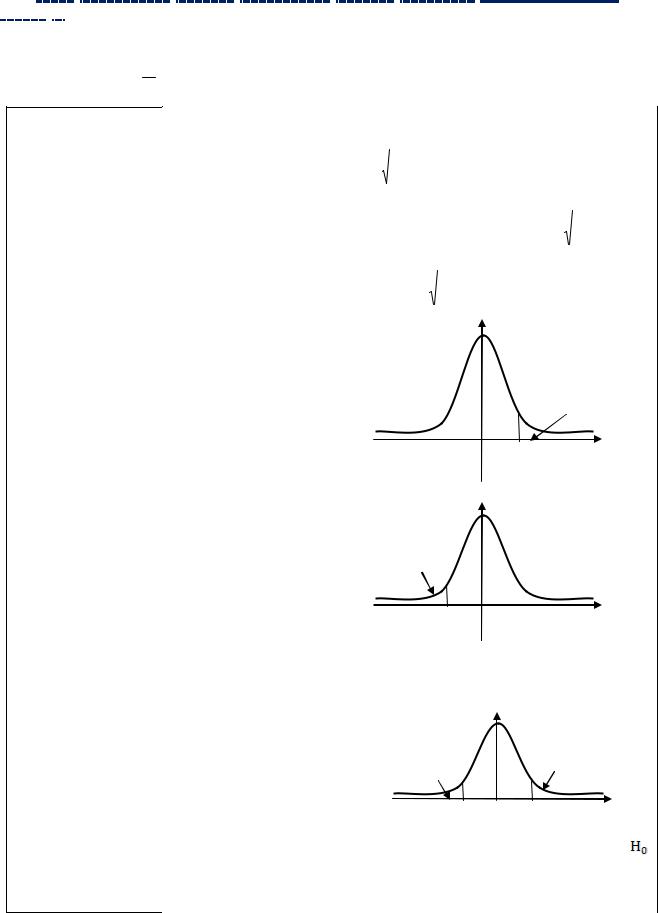
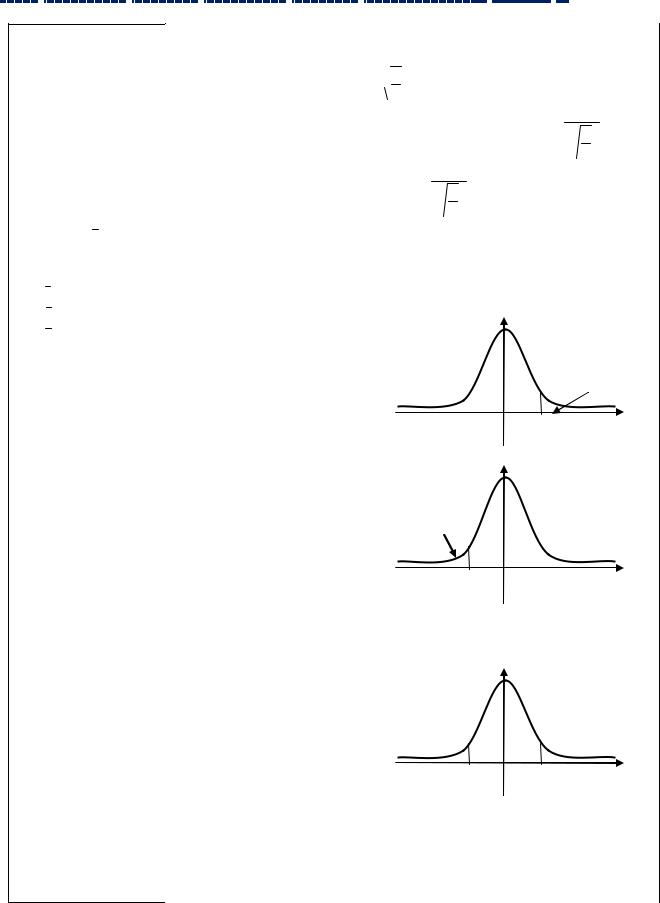
Ошибкой I рода называется ситуация, когда была принята альтернативная гипотеза, хотя была справедлива гипотеза Но (нулевая). Вероятность совершения ошибки I рода: P(H1/ Ho) P{Zвыб Vкр / Но} . Эта формула означает, что
гипотеза Но отвергается с вероятностью , хотя она была верна.
Ошибкой II рода называется ситуация, когда была верна альтернативная гипотеза, а приняли гипотезу Но (нулевую).Вероятность совершения ошибки II рода:
P(Hо / H1) P{Zвыб ОПР/ Н1} . |
Эта формула означает, |
что принимается |
|||||||||||||||||||||||||||||||||||||
гипотеза Но с вероятностью , хотя верна гипотеза Н1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Замечание: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
o |
Значение вероятности задается (достаточно малое),а значение |
|||||||||||||||||||||||||||||||||||||
|
|
вероятности необходимо находить. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
o |
Принято обозначение : |
(k) 1 - мощность критерия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
o |
Вероятность |
того, |
что |
|
|
ошибка |
I |
рода |
не |
|
|
|
|
совершена: |
||||||||||||||||||||||||
|
|
P(Ho / Ho) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
Вероятность |
того, |
что |
|
ошибка |
II |
рода |
не |
|
|
|
|
совершена: |
|||||||||||||||||||||||||
|
|
P(H1/ H1) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
oВ обоих случаях принято, что под чертой в скобках указывается верная гипотеза.
Связь между ошибками I и II рода
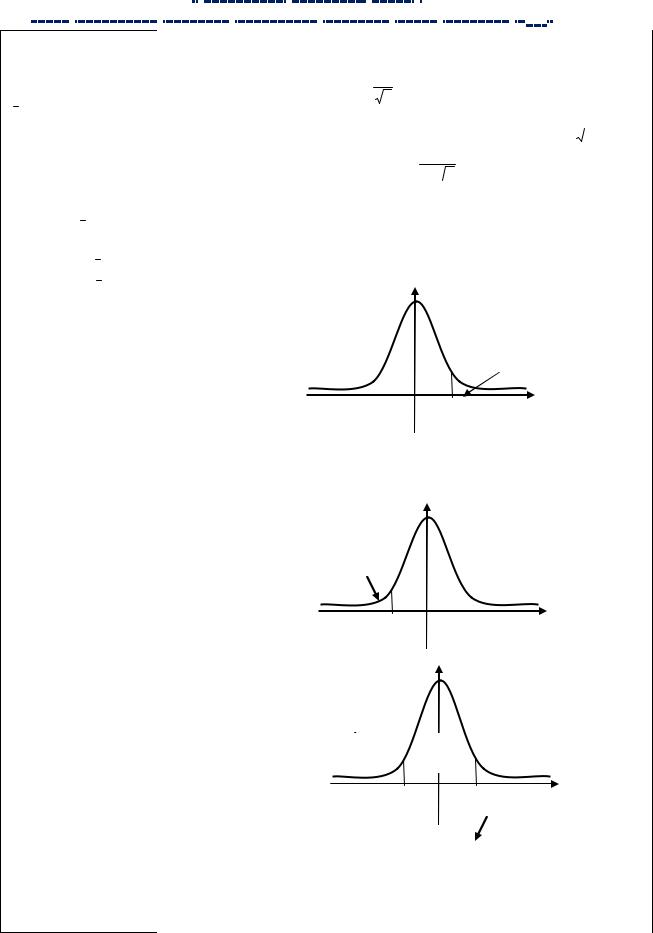
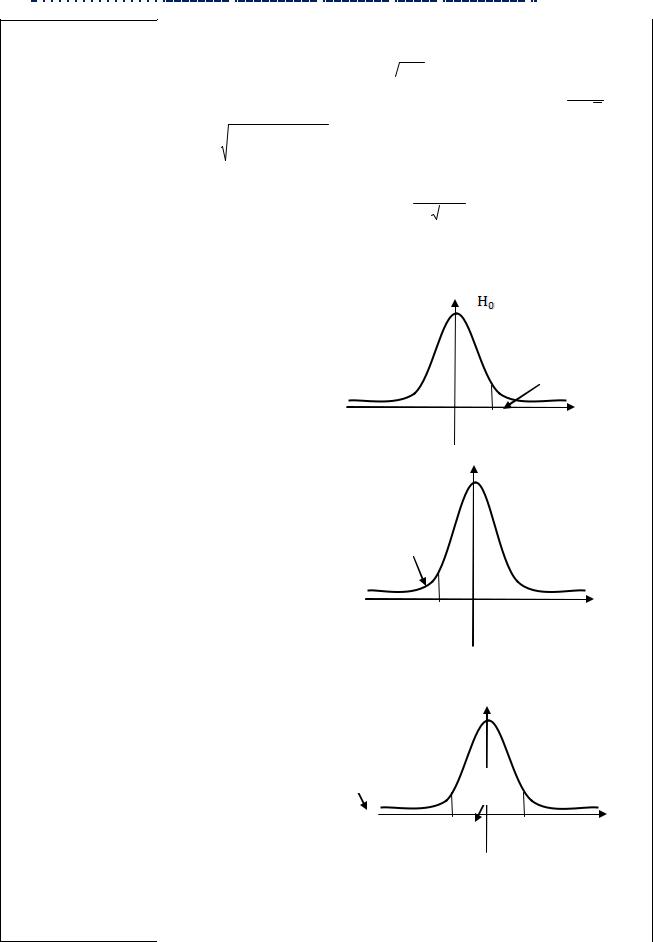
Для того, чтобы проверяемая гипотеза была достаточно обоснованно отвергнута, уровень значимости выбирают достаточно малым; в практике: 0,01; 0,001. Напротив, если делается вывод о принятии гипотезы, то уровень значимости не должен быть очень малым, т.к. в этом случае расширяется область допустимых значений V \ Vкр , и даже при неверной гипотезе статистика Z критерия может
попасть в эту область за счет случайных колебаний. Будет совершена ошибка второго рода. Уровень значимости в этом случае можно взять равным 0,5; 0,1. Чем меньше уровень значимости, тем меньше вероятность забраковать верную гипотезу,
Стр. 121
т.е. совершить ошибку первого рода, но при этом увеличивается вероятность принятия неверной гипотезы, т.е. совершения ошибки второго рода.
|
Нулевая гипотеза |
Результаты решения относительно |
|||
|
H0 |
нулевой гипотезы |
|||
|
|
Н0 |
|||
|
|
|
|||
|
|
|
|
|
|
|
|
Отклонена |
|
|
Принята |
|
Верна |
Ошибка 1-го рода, |
|
|
Правильное решение, |
|
|
её вероятность |
|
|
его вероятность |
|
|
Р(Н1/ Н0)= |
|
|
Р(Н0/ Н0)=1- |
|
Неверна |
Правильное решение, |
|
|
Ошибка 2-го рода, |
|
|
его вероятность |
|
|
её вероятность |
|
|
Р(Н1/ Н1)=1- |
|
|
Р(Н0/ Н1)= |
Стр. 122

Задача 7
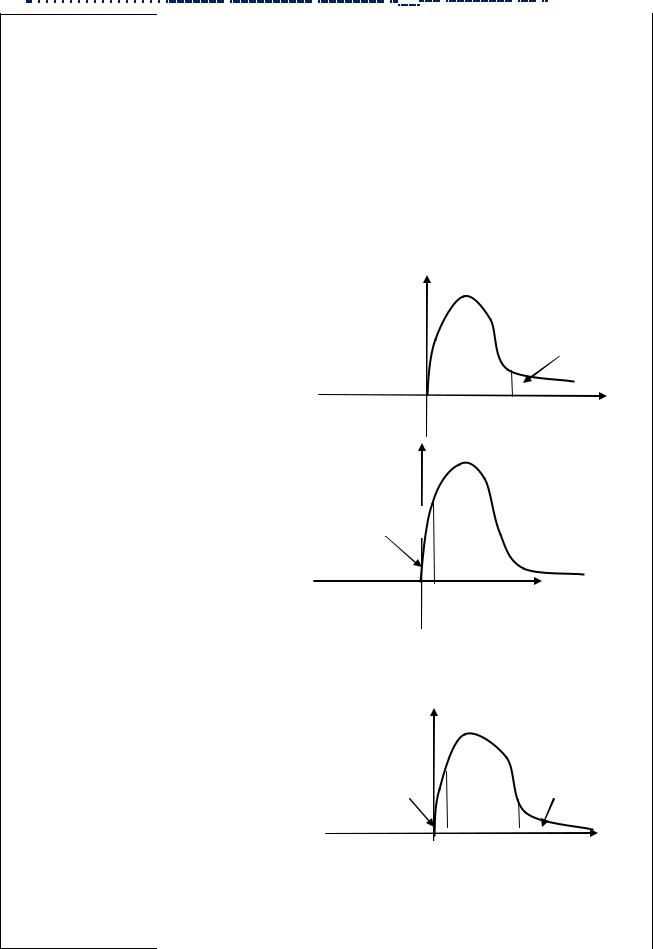
Магазин хочет закупить большую партию мобильных телефонов. Поставщик данной фирмы утверждает, что доля бракованных телефонов составляет 5%. По некоторым «разведанным» данным директор предполагает, что доля дефектных телефонов составит 10%. Между поставщиком и магазином было составлено следующее соглашение: случайным образом отбирают и проверяют 10 телефонов. Магазин закупит партию, если при проверке будет обнаружено не более одного бракованного телефона, в противном случае цена закупки будет снижена, либо партия не будет закуплена.
Вопросы:
1.Сформулируйте эту задачу в терминах теории проверки статистических гипотез.
2.Какова статистика критерия, область значений, критическая область, какое распределение этой статистики?
3.В чем состоят проверяемая и альтернативная гипотезы?
4.В чем состоят ошибки первого и второго рода и каковы их вероятности
|
Решение |
|
1. Х- число бракованных телефонов (распределение Бернулли). |
||
o |
Событие A - телефон бракованный. |
P( A) P0 |
|
||
o |
H0 : P0 0,05 , H0 - гипотеза поставщика, которую мы проверяем. |
|
oH1 : P0 0,1 H1 - гипотеза директора магазина (альтернативная гипотеза).
2.Pk P{X k} Cmk pk qm k ( q 1 p )
o V {0,1, 2,..,10}- область ограничений статистики Х
o
X i |
|
|
0 |
|
1 |
|
2 |
|
… |
k |
… |
|
|
… |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pi |
|
|
q10 |
|
10q9 p |
|
… |
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Ошибка 1 рода: P(H1 / Ho ) |
|
|
|
|
|
|
|
|
||||||||
|
Партия закуплена на условиях магазина, в то время, как верно утверждение |
|||||||||||||||
поставщика. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Это |
значит, |
что |
p 0, 05 ( q 0,95 ) |
и при |
проверке оказалось |
более |
одного |
||||||||
бракованного телефона. |
|
|
|
|
|
|
|
|
|
|
|
|||||
P(H / H |
) P P ... P 1 P P 1 (0,95)10 10(0,95)9 0, 05 0, 086 |
|
|
|
||||||||||||
1 |
0 |
2 |
|
3 |
10 |
0 |
|
1 |
|
|
|
|
|
|
|
|
Ответ: 0, 086 – вероятность ошибки 1 рода.
4. Ошибка 2 рода: P(H0 / H1)
Партия закуплена магазином на условиях поставщика, в то время, как верно утверждение директора магазина.
Выборочное значение попало в область принятия решений, то есть число бракованных телефонов не превысило одного.
p 0,1 |
P(H |
0 |
/ H ) P{X 0} P{X 1} (0,9)10 |
10(0,9)9 0,1 0,349 0,387 0, 736 |
|
|
1 |
|
|
q 0, 9 |
0, 736 |
|
||
Стр. 129

Задача 8 (самостоятельно)
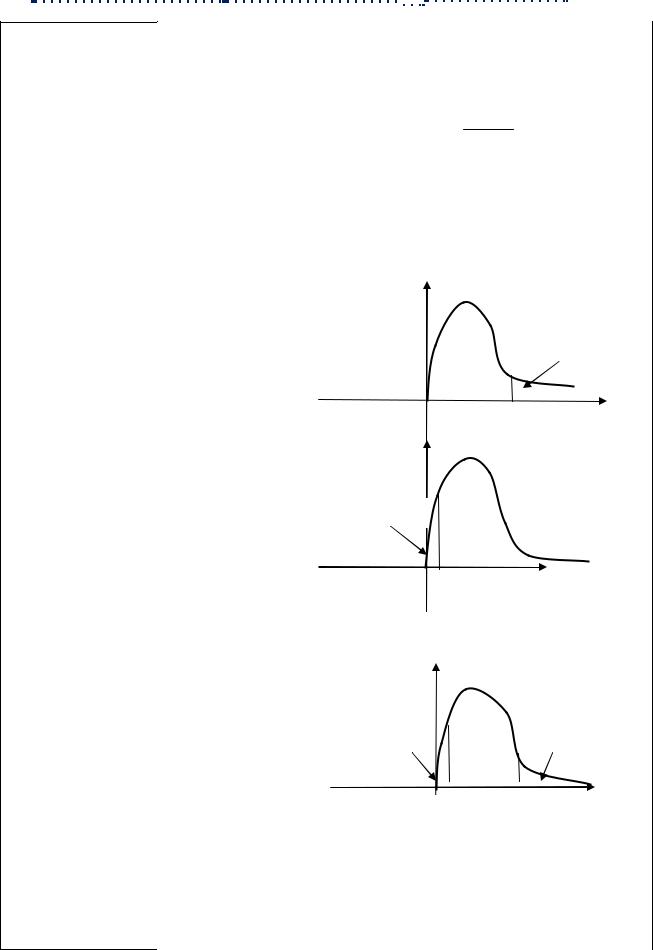
Проверка функционирования устройства оценивается специальным тестом. Если устройство функционирует правильно, то вероятность прохождения теста равна 0,99; в противном случае вероятность прохождения теста равна 0,4. Устройство допускается к работе, если тест проходит 5 раз подряд. В предположении, что число прохождений теста подчиняется биномиальному распределению, ответить на вопросы:
1.Какова область изменения и критическая область статистики критерия? Какое распределение имеет статистика критерия?
2.Как сформулировать нулевую гипотезу, если ошибка первого рода состоит в отклонении правильно функционирующего устройства?
3.Какова альтернативная гипотеза и в чем состоит ошибка второго рода?
4.Чему равны вероятности ошибок первого и второго рода.
Решение
1. Биномиальное распределение |
P{X k} Ck |
pk qm k , m 5 |
m |
|
|
|
|
|
A -тест прошел, P( A) p |
|
|
H0 - устройство функционирует правильно, p 0,99
H1 - устройство функционирует неправильно, p 0, 4
2.Ошибка 2 рода - принятие неправильного функционирующего устройства.
V {0,1, 2,3, 4,5}
3.Vкр {0,1, 2,3, 4}
Ответ:
Стр. 130


 n
n 



 n
n n
n