
- •34. Несжимаемая жидкость. Уравнение непрерывности для несжимаемой жидкости.
- •35.Уравнение Бернулли. Какой из законов сохранения выражает уравнение Бернулли?
- •36. Макроскопическая система. Что называется молем вещества? Молярная масса, число Авогадро, его величина и размерность.
- •37. Тепловое равновесие.
- •38. Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа.
- •39. Связь средней кинетической энергии молекул газа с его температурой.
- •40. Постоянная Больцмана, ее величина, размерность, физический смысл.
- •41. Уравнение Клапейрона - Менделеева. Физический смысл универсальной газовой постоянной.
- •42. Давление и температура с точки зрения молекулярно кинетической теории.
- •43.Среднеквадратичная скорость молекул газа.
- •44.Уравнение изобарного процесса. Его график в координатах pv, pt, vt.
- •45.Уравнение изохорного процесса. Его график в координатах pv, pt, vt.
- •46.Уравнение изотермического процесса. Его график в координатах pv, pt, vt.
- •48.Внутренняя энергия.
- •49. Формула работы для элементарного квазистационарного процесса. Геометрическое изображение работы в координатах pv.
- •50. Адиабатический процесс. Уравнение Пуассона.
- •51.Первое начало термодинамики. Теплоемкость тела, её единицы измерения. Молярная и удельная теплоемкости.
- •52.Первый закон термодинамики для изохорного процесса. Внутренняя энергия идеального газа.
- •53. Первый закон термодинамики для изобарного процесса.
- •54. Формула Майера для теплоемкостей.
- •55.Первый закон термодинамики для изотермического и для адиабатического процессов.
- •56.Второе начало термодинамики.
- •57. Энтропия. Обратимые и необратимые процессы. Изменение энтропии замкнутой системы при необратимом процессе.
- •Обратимый цикл Карно
- •Необратимый цикл Карно
- •58. Циклические процессы.
- •59.Функция распределения физической величины. Распределение Максвелла для скоростей молекул газа.
- •60. Изменение распределения Максвелла при изменении температуры газа. Вид распределения Максвелла в зависимости от молекулярной массы газа.
- •61. Среднеквадратичная скорость. Наиболее вероятная скорость молекул.
- •62. Распределение Больцмана
- •63. Барометрическая формула
- •64. Закон сохранения электрического заряда. Элементарный электрический заряд.
- •65. Закон Кулона (в системе си).
- •66. Напряженность электрического поля, единицы измерения. Напряженность поля точечного заряда.
- •67. Силовые линии (линии напряженности) электрического поля. Однородное поле
53. Первый закон термодинамики для изобарного процесса.
В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением
|
A = p(V2 – V1) = pΔV. |
Первый закон термодинамики для изобарного процесса дает:
Q = U(T2) – U(T1) + p(V2 – V1) = ΔU + pΔV.
|
|
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.
54. Формула Майера для теплоемкостей.
Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула справедлива для любого процесса.
Для
произвольной идеальной массы газа:
![]()
При
изобарическом процессе, кроме увеличения
внутренней энергии, происходит совершение
работы газом:
![]()
![]()
Из основного уравнения
молекулярно-кинетической теории ![]() .
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
.
При изобарическом процессе Р = const.
Следовательно, из (4.2.7) получим:
![]()
Это уравнение Майера для одного моля газа.
Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.
Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
Полезно знать формулу Майера для удельных теплоёмкостей:
|
|
|
|
|
55.Первый закон термодинамики для изотермического и для адиабатического процессов.
Изотермический
процесс
Первый
закон термодинамики для изотермического
процесса выражается соотношением:
Q=A
Количество
теплоты Q, полученной газом в процессе
изотермического расширения, превращается
в работу над внешними телами. При
изотермическом сжатии работа внешних
сил, произведенная над газом, превращается
в тепло, которое передается окружающим
телам.
Наряду
с изохорным, изобарным и изотермическим
процессами в термодинамике часто
рассматриваются процессы, протекающие
в отсутствие теплообмена с окружающими
телами. Сосуды с теплонепроницаемыми
стенками называютсяадиабатическими
оболочками, а процессы расширения или
сжатия газа в таких сосудах
называются адиабатическими.
Работа
в изотермическом процессе ![]() .
Интегрируя, получим,
.
Интегрируя, получим,

![]() .
Адиабатный
процесс
В адиабатическом
процессе Q = 0; поэтому первый
закон термодинамики принимает вид:
A = –ΔU,
.
Адиабатный
процесс
В адиабатическом
процессе Q = 0; поэтому первый
закон термодинамики принимает вид:
A = –ΔU,
 т. е.
газ совершает работу за счет убыли его
внутренней энергии.
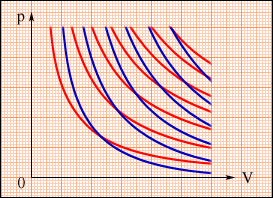
На
плоскости (p, V) процесс адиабатического
расширения (или сжатия) газа изображается
кривой, которая называется адиабатой.
При адиабатическом расширении газ
совершает положительную работу (A > 0);
поэтому его внутренняя энергия уменьшается
(ΔU < 0). Это приводит к понижению
температуры газа. Вследствие этого
давление газа при адиабатическом
расширении убывает быстрее, чем при
изотермическом расширении.
т. е.
газ совершает работу за счет убыли его
внутренней энергии.
На
плоскости (p, V) процесс адиабатического
расширения (или сжатия) газа изображается
кривой, которая называется адиабатой.
При адиабатическом расширении газ
совершает положительную работу (A > 0);
поэтому его внутренняя энергия уменьшается
(ΔU < 0). Это приводит к понижению
температуры газа. Вследствие этого
давление газа при адиабатическом
расширении убывает быстрее, чем при
изотермическом расширении.
В термодинамике выводится уравнение адиабатического процесса для идеального газа. В координатах (p, V) это уравнение имеет вид: pVγ = const.
Это
соотношение называют уравнением
Пуассона. Здесь γ = Cp / CV –
показатель адиабаты, Cp и CV –
теплоемкости газа в процессах с постоянным
давлением и с постоянным объемом. Для
одноатомного газа 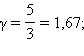 для
двухатомного
для
двухатомного для
многоатомного
для
многоатомного![]() Работа
газа в адиабатическом процессе просто
выражается через температуры T1 и T2 начального
и конечного состояний:
A = CV(T2 – T1).
в)
Работа в адиабатном процессе
Работа
газа в адиабатическом процессе просто
выражается через температуры T1 и T2 начального
и конечного состояний:
A = CV(T2 – T1).
в)
Работа в адиабатном процессе ![]()
![]() .
Интегрируя, получим:
.
Интегрируя, получим:
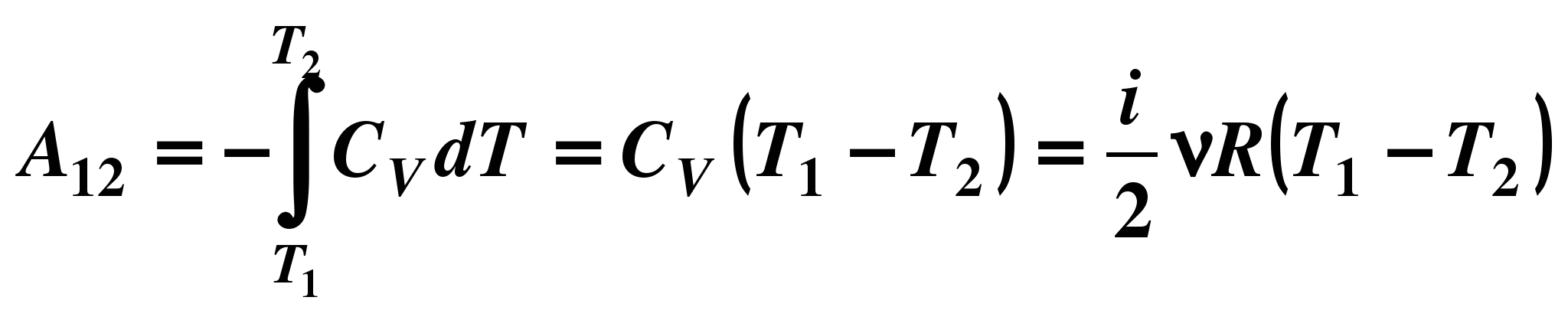 .
.
