
Econometrics1_enie_aaee_iia_
.pdfRлевая R Rправая
6.Все расчеты выполняются в MS Excel. Отчет готовиться в MS Word с описанием основных шагов выполнения данной лабораторной работы и интерпретацией полученных результатов.
7.Подготовленный отчет сдается через электронную систему обучения ГОУ ВПО КГТЭИ.
1.4.Лабораторная работа № 2
На основе данных таблицы данных (см. Приложение) для соответствующего варианта :
1.Построить линейное и нелинейное (экспонентциальное) уравнения регрессии по любой паре экономических показателей, анализируемых в 1 лабораторной работе.
2.Проверить значимость уравнений регрессии и отдельных коэффициентов линейного уравнения.
3.Определить лучшее уравнение регрессии на основе средней ошибки аппроксимации.
4.Построить интервальный прогноз для значения x = xmax для линейного уравнения регрессии.
5.Определить средний коэффициент эластичности.
Краткие указания к выполнению лабораторной работы с помощью программных средств MS Excel
1. Для оценки неизвестных параметров регрессии необходимо воспользоваться двумя метода, имеющимися в MS Еxcel:
А) Случай линейной регрессии. В главном меню выбирается: Сервис Анализ данных Регрессия. В качестве входного интервала Y указывается диапазон всех значений y (соответствующий столбец) исходной таблицы, входного интервала X – все значения выбранного х (Рис. 1.6.)
21
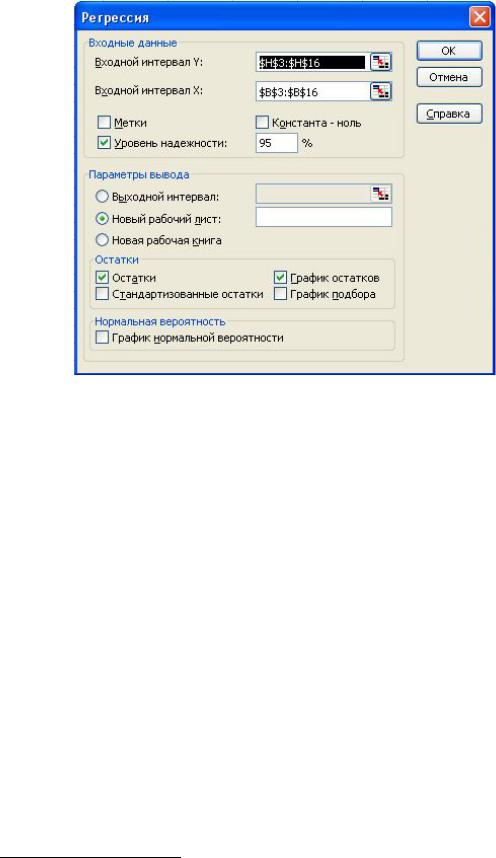
Рис. 1.6. Использования сервисного метода "Регрессия" в MS Excel
При этом, выделяются опции "Остатки" и "График остатков". После выделения всех необходимых опций на новом рабочем листе будут указаны расчетные оценки коэффициентов регрессии, статистик качества регрессии (см. п. 1.1.), таблица значений предсказанного yˆ , остатков регрессии и график остатков (Рис. 1.7).
В примере (Рис. 1.7.) оценки коэффициентов регрессии a и b равны, соответственно, 7,193 и 0,0734.
Б) Случай нелинейной (экспоненциальной) регрессии. Для построения экспоненциальной регрессии вида y a1ea2x необходимо к исходной таблице добавить столбец значений предсказанного yˆ , которые находиться по следующей формуле MS Excel: =а1*exp(a2*x), задать начальные значения a1, a2 в соответствующих ячейках рабочего листа1, добавить столбец значений ошибок, рассчитанных по формуле (y yˆ)2 (в MS Excel: =(y- yˆ )^2), а также подсчитать сумму значений остатков в соответствующей ячейке (Рис. 1.8).
1 Начальное значение для a2 выбирается досточно малым числом. Например: 0,001
22
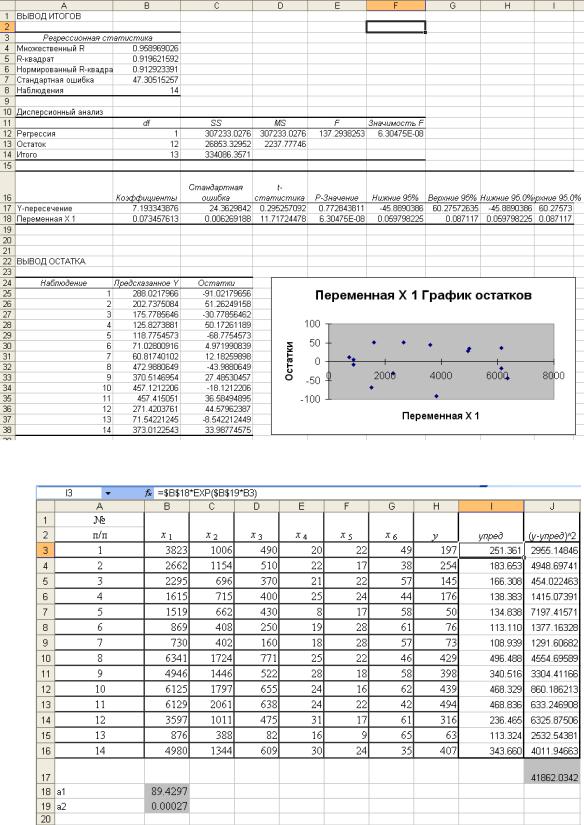
Рис. 1.7. Лист вывода итогов после выполнения линейной парной регрессии в
MS Excel
Рис. 1.8. Пример оформления рабочего листа для экспоненциальной регрессии
23
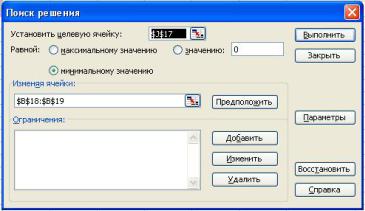
После этого этапа предварительной подготовки, в главном меню выбирается: Сервис Поиск решения (Рис. 1.9). В качестве целевой ячейки указывается ссылка на ячейку, где подсчитана сумма остатков. При этом, это значение необходимо минимизировать, т.е. необходимо выделить соответствующую опцию (Рис. 1.9). Далее, необходимо провести оптимизацию, изменяя ячейки в которых указаны значения коэффициентов регрессии a1, a2 (Рис.1.9). Фактически, на этом этапе проводится оценка коэффициентов регрессии, минимизирующих суммарную ошибку регрессии на базе метода наименьших квадратов.
Рис. 1.9. Пример использования процедуры "Поиска решения" для нахождения оценок коэффициентов нелинейной регрессии.
2.Для случая линейной регрессии необходимо воспользоваться расчетными данными рабочего листа вывода итогов. Для случая нелинейной регрессии необходимо рассчитать все характеристики, используя возможности MS Excel, вручную. После этого, применить F-критерий Фишера и t-критерий Стьюдента
(см. п.1.1).
3.Рассчитать среднюю ошибку аппроксимации для обоих случаев и сравнить значения.
4.Построить интервальный прогноз для значения x = xmax для линейного уравнения регрессии.
5.Рассчитать средний коэффициент эластичности для обоих уравнений и проинтерпретировать эти значения.
6.Подготовить отчет в MS Word с описанием основных шагов выполнения данной лабораторной работы и интерпретацией полученных результатов.
7.Подготовленный отчет сдается через электронную систему обучения ГОУ ВПО КГТЭИ
24
Глава 2. Множественные корреляции и регрессии
2.1. Теоретические основы
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии
Множественная регрессия - уравнение связи с несколькими независимыми переменными:
|
y = f(x1, x2,...,xp), |
где |
у - зависимая переменная (результативный признак); |
x1, x2,...,xp - независимые переменные (факторы).
Для построения уравнения множественной регрессии чаще используются следующие функции:
•линейная - у = a + b1∙x1+b2∙x2+…+bp∙xp+ε;
•степенная - у= а ∙x1b1 x2b2 ... xbpp ,
•экспонента - у = a∙ea b1 x1 b2 x2 ... bp xp ;
• гипербола - у = |
1 |
. |
|
a b1 x1 b2 x2 ... bp xp
Можно использовать и другие функции, приводимые к линейному виду.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то емунужно придать количественную определенность.
25
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Отбор факторов производится на основе качественного теоретикоэкономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии.
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если rxixj 0,7. Если факторы явно коллинеарны, то они
дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов (см. соответствующий критерий ниже).
Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.
При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено,
26
то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F -критерий меньше табличного значения.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
y na b1 x1 b2 x2 |
... bp xp, |
|
|
|
|||||||
|
yx a x b x2 |
b x x |
|
|
b |
x |
|
x , |
|||
|
2 |
p |
|||||||||
1 |
1 1 1 |
2 |
1 |
|
p |
|
1 |
||||
.......................................................................................... |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
a x |
|
b x x |
|
b x |
|
x |
|
|
b |
x |
2 |
. |
|
|
p |
p |
p |
2 |
p |
p |
||||||||||
|
|
1 1 |
2 |
|
|
p |
|
|
||||||||
Для ее решения может быть применён метод определителей:
a |
a |
, b |
b |
b |
|
|
bp |
, |
|
|
1 |
,..., |
p |
|
|
||||
|
|
|
|||||||
|
1 |
|
|
|
|
||||
|
n |
|
x1 |
|
|
x2 ... |
xp |
|
|
|
|
|||||||
|
x |
|
x2 |
|
|
x |
2 |
x ... |
x |
p |
x |
|
||||||
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
||||
где |
x |
2 |
x x |
2 |
|
x2 ... |
x |
p |
|
x |
2 |
определитель матрицы |
||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
||||||
|
........................................ |
|
|
|
||||||||||||||
|
x |
p |
x x |
p |
x |
2 |
x |
p |
... |
x |
2 |
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
p |
|
|
||||||
Δa1, Δb1… ,Δbp - частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Другой вид уравнения множественной регрессии - уравнение регрессии в стандартизованном масштабе:
ty=β1tx1 + β2tx2 +…+βptxp ,
27

где ty |
|
y |
y |
, tx |
|
|
xl |
x |
l |
стандартизованные переменные; |
|
|
|
x |
|||||||
|
|
y |
l |
|
|
|||||
|
|
|
|
|
|
|
l |
|
||
βl - стандартизованные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β- коэффициенты) определяются из следующей системы уравнений:
r |
|
|
|
r |
r |
... |
|
r , |
|||
|
yx1 |
|
1 |
|
2 x2x1 |
3 x3x1 |
|
|
p xpx1 |
||
ryx2 |
1rx2x1 |
2 |
3rx3x2 |
... |
prxpx2 , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
.................................................................. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
r |
|
r |
r |
... |
|
p |
. |
|||
|
yxp |
|
1 xpx1 |
|
2 xpx2 |
3 x3xp |
|
|
|
||
Связь коэффициентов множественной регрессии b, со стандартизованными коэффициентами β, описывается соотношением
bl l y ,
xl
Параметр а определяется как а = y b1x1 b2x2 ... bpxp.
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле
|
|
|
b |
|
|
x |
j |
. |
||
Э |
|
|
|
|||||||
|
yxj |
j |
|
|
|
|
||||
|
|
|
y |
|||||||
|
|
|
|
|
|
|||||
Частные уравнения регрессии - это уравнения регрессии, которые связывают результативный признак с соответствующим фактором xi при закреплении остальных факторов на среднем уровне. В развернутом виде систему можно переписать в виде:
28

yx x ,x ,...,x |
m |
a b1x1 |
b2 |
x |
2 |
b3 |
x3 |
... |
bm |
x |
m , |
|||||||||
|
1 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx2 x1,x3 ,...,xm |
a b1 |
x1 |
b2x2 |
b3 |
x3 |
... |
bm |
x |
m , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
........................................................................ |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
xm x1,x2 |
,...,xm 1 |
a b |
x |
b |
x |
b |
x |
.. |
. b x . |
||||||||||
|
1 |
|
1 2 |
|
2 3 |
|
3 |
|
m m |
|||||||||||
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем
yx1 x2 ,x3 ,...,xm A1 b1x1,
yx2 x1,x3 ,...,xm A2 b2x2,
................................
yxm x1,x2 ,...,xm 1 Am bmxm,
где
A1 a b2 |
x |
2 b3 |
x3 |
... bm |
x |
m, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
...a b1x1 b3x3 |
bmxm |
, |
|
|
|
||||||||||||||
.............................................. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A a b |
x |
b |
x |
b |
x |
... |
b |
x |
m 1 |
. |
||||||||||
m |
1 1 2 2 |
3 3 |
|
|
|
|
m 1 |
|
|
|||||||||||
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
Эyx |
bi |
|
|
xi |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|||
|
i |
yx x x |
x |
|
,x |
, |
,x |
|
|
|
|
|
i 1 |
p |
|||||||
|
|
i |
1, 2, |
, |
i 1 |
|
|
|||
где bi – коэффициент регрессии для фактора xi в уравнении множественной регрессии,
yxi x1,x2,...xi 1,xi 1,...,xm – частное уравнение регрессии.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
29
|
|
|
|
|
|
2 |
|
|
R yx |
1 |
x |
2 |
, |
x p |
1 |
yост |
|
|
||||||||
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
|
|
y |
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
Ryx1x2 , ,xp ryx1 |
i |
|
. |
1, p |
Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде
Ryx x |
, |
,x |
p |
irxy |
. |
1 2 |
|
|
|
i |
При линейной зависимости коэффициент множественной корреляции
можно определить через матрицу парных коэффициентов корреляции:
Ryx x |
|
|
1 |
r |
|
, |
x |
|
|
||||
rx ,...,x |
|
|||||
1 2, |
, |
p |
|
|
|
|
|
|
|
|
p |
||
|
|
|
1 |
|||
где
|
1 |
|
ryx |
ryx |
2 |
|
. |
ryx |
p |
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
ryx |
|
1 |
|
|
rx x |
|
... |
rx x |
p |
|
|||
|
1 |
|
|
|
1 |
2 |
|
1 |
|
|
|
|||
r |
ryx |
2 |
rx x |
1 |
|
|
... |
rx |
x |
p |
|
|||
|
|
|
2 |
1 |
|
|
|
|
2 |
|
|
|
||
|
............................................ |
|
||||||||||||
|
ryx |
p |
rx |
p |
x |
rx |
p |
x |
... |
1 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|||
определитель матрицы парных коэффициентов корреляции;
30
