
Econometrics1_enie_aaee_iia_
.pdf
наиболее часто используемых типов уравнений регрессии:
Таблица 1.1 Формулы расчета средних коэффициентов для наиболее часто встречающихся
уравнений регрессий
Вид функции, y |
|
|
|
Первая |
|
|
Средний |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
коэффициент |
|
|
Линеаризация |
|||||||||||||||||||||||||||||||||||
производная, y |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
эластичности, Ý |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y a b x |
|
|
|
|
b |
|
|
|
|
|
b |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|||||||||||||||
|
|
|
|
|
|
|
a b |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y a b x c x2 |
|
|
|
b 2c x |
|
b 2c |
x |
|
x |
|
|
|
Х1=х, Х2=х2 |
|||||||||||||||||||||||||||||
|
|
|
a b |
x |
c |
x |
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
y a |
b |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
Х=1/х,Y=y |
||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
a |
x |
b |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
y a xb |
|
|
|
a b xb 1 |
|
|
|
|
|
|
|
b |
|
Х=lnх,Y=lny |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y a bx |
|
|
a lnb bx |
|
|
|
|
|
x |
lnb |
|
Х=х,Y=lny |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
y a b ln x |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
b |
|
|
Х=lnх,Y=y |
||||||||||||||||||||||||
|
|
|
|
x |
|
|
a b ln |
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
y ea bx |
|
|
|
bea bx |
|
|
|
|
|
x |
b |
|
Х=х,Y=lny |
|||||||||||||||||||||||||||||
y |
|
a |
|
a b c e c x |
|
|
|
|
b c |
x |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
1 b e c x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 b e c x |
|
|
|
|
|
|
|
b ec |
x |
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y a b x |
|
|
a b x 2 |
|
|
a b |
x |
|
|
|
|
|
|
|
|
Х=х,Y=1/y |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
(y y )2 (yx y)2 (y yx )2 ,
где (y y)2 - общая сумма квадратов отклонений;
y y 2 - сумма квадратов отклонений, обусловленная регрессией
11

(«объясненная»
или «факторная»);
y yx 2 - остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации
R2
R2 yx y 2 .
y y 2
Коэффициент детерминации - квадрат коэффициента или индекса корреляции.
F-mecm - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя
тесноты связи. Для этого |
выполняется сравнение фактического Fфакт и |
|||
критического |
(табличного) |
Fтабл значений |
F-критерия |
Фишера. |
Fфакт определяется из соотношения значений факторной и остаточной дисперсий,
рассчитанных на одну степень свободы:
F |
y |
y |
2 /m |
|
rxy2 |
(n 2), |
|
y y 2 /(n m 1) |
1 rxy2 |
||||||
факт |
|
|
|||||
где п - число единиц совокупности;
т - число параметров при переменных х.
Fтабл - это максимально возможное значение критерия под влиянием
случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то Н0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости
12
коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
t |
b |
|
b |
;t |
a |
|
a |
;t |
r |
|
r |
. |
|
|
|
||||||||||
|
|
m |
|
m |
|
m |
||||||
|
|
|
b |
|
|
a |
|
|
r |
|||
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y yx 2 / n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
m |
|
|
|
|
|
|
|
|
|
|
Sост2 |
|
|
Sост |
|
|
|
|
; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
2 |
|
|
x |
|
2 |
|
|
|
|
|
|||||||||||||||||||||||
b |
|
|
|
x |
|
|
|
|
x |
|
x n |
|
||||||||||||||||||||||||
|
|
y yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
m |
|
|
|
x2 |
|
|
S |
2 |
|
x2 |
|
S |
|
|
|
|
x2 |
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a |
|
n 2 |
n x |
x |
2 |
|
|
|
|
|
ост n2 x2 |
|
|
|
ост |
n x |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
m |
|
|
xy |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
rxy |
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Сравнивая фактическое и критическое (табличное) значения t-статистики -
tта6л и tфакт - принимаем или отвергаем гипотезу Н0 о равенстве нулю соотвествующих коэффициентов регрессии.
Для проверки значимости коэффициента корреляции необходимо возпрользоваться следующим алгоритмом.
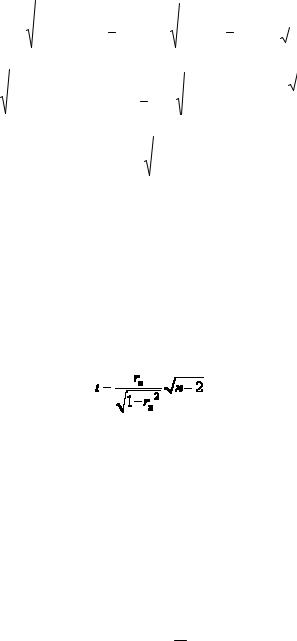
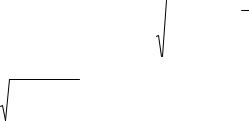
Собственное распределение величины r (коэффициента корреляции) довольно сложное, поэтому необходимо применить преобразование:
При нулевой гипотезе о равентсве нулю коэффициента корреляции выборочное распределение статистики t есть распределение Стьюдента с n-2 степенями свободы. Если tфакт, полученное по формуле, указанной выше, меньше tтабл, тогда нулевая гипотеза принимается. Иначе нулевая гипотеза отвергается и принимается альтернативная гипотеза о неравенстве нулю коэффициента корреляции.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:
tr2 tb2 
 F
F
13

Если tта6л < tфакт то H0 отклоняется, т.е. а, b и rху не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tта6л > tфакт, то гипотеза H0 не отклоняется и признается случайная природа формирования a, b или rху.
Для расчета доверительного интервала определяем предельную ошибкудля каждого показателя:
a tтаблma, b tтаблmb
Формулы для расчета доверительных интервалов имеют следующий вид:
a a a; amin a a; amax a a;b b b; bmin b b; bmax b b.
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
В случае построения доверительных границ для коэффициента корреляции необходимо воспользоваться z-преобразованием Фишера. А именно:
1. Рассчитать фактическое значение z по следующей формуле:
1 1 r
zфакт 2 ln1 r
2. Рассчитать среднюю ошибку z:
mz |
|
|
1 |
|
|
|
|||
n 3 |
||||
|
|
|
3. Построить доверительный интервал для z, а именно:
zфакт tтабmz Z zфакт tтабmz
или
Zлевая Z Zправая
4. Левую и правую границу этого интервала преобразовать по формуле:
R |
|
|
e2Zлевая 1 |
;R |
|
e2Zправая 1 |
|
|
левая |
|
e2z 1 |
правая |
|
e2z 1 |
|
5. Окончательно, с вероятностью P=1- можно утверждать, что истинное значение коэффиицента корреляции будет лежать в пределах:
14
Rлевая R Rправая
Чтобы регрессионный анализ, основанный на обычном МНК, давал наилучшие результаты, случайный член должен удовлетворять четырем условиям Гаусса — Маркова.
Математическое ожидание случайного члена равняется нулю, т.е. он является несмещенным. Если уравнение регрессии включает постоянное слагаемое, то естественно считать выполненным такое требование, поскольку это постоянное слагаемое и должно учитывать любую систематическую тенденцию в значениях переменной у, которую, напротив, не должны содержать объясняющие переменные уравнения регрессии.
Дисперсия случайного члена постоянна для всех наблюдений.
Ковариация значений случайных величин, образующих выборку, должна быть равна нулю, т.е. отсутствует систематическая связь между значениями случайного члена в любых двух конкретных наблюдениях. Случайные члены должны быть независимы друг от друга.
Закон распределения случайного члена должен быть независим от объясняющих переменных. Более того, во многих применениях объясняющие переменные не являются стохастическими, т.е. не имеют случайной составляющей. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.
Вместе с указанными условиями Гаусса— Маркова предполагают также, что случайный член имеет нормальное распределение. Оно справедливо при весьма широких условиях и основывается на так называемой центральной предельной теореме (ЦПТ). Суть этой теоремы в том, что если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не оказывает преобладающего влияния на общий результат, то такая результирующая случайная величина будет описываться приблизительно нормальным распределением. Эта близость к нормальному распределению позволяет использовать для получения оценок нормальное распределение и являющееся, в известном смысле, его обобщением распределение Стьюдента, которое заметно отличается от нормального, главным образом, на так называемых «хвостах», т.е. при малых значениях объема выборки. Важно также, что если случайный член будет распределен нормально, то и коэффициенты регрессии также будут распределены по нормальному закону.
15
Установленная регрессионная кривая (уравнение регрессии) позволяет решить задачу так называемого точечного прогноза. В таких расчетах берется некоторое значение х вне исследованного интервала наблюдений и подставляется в правую часть уравнения регрессии (процедура экстраполяции). Поскольку уже известны оценки для коэффициентов регрессии, то можно рассчитать соответствующее взятому значению величины х значение объясняемой переменной у. Естественно, что в соответствии со смыслом предсказания (прогноза) расчеты проводятся вперед (в область будущих значений).
Прогнозное значение ур определяется путем подстановки в уравнение
регрессии |
yx a b xсоответствующего (прогнозного) значения |
хр. |
Вычисляется |
средняя стандартная ошибка прогноза myp |
|
myp = ост |
|
1 |
|
xp |
x |
2 |
|
|
, |
||
|
|
|
|
|
|
2 |
|||||
n |
|
x x |
|||||||||
|
|
|
|
|
|
||||||
y yˆ 2
где ост ; n m 1
и строится доверительный интервал прогноза:
y |
yp |
y |
; y |
pmin |
yp |
y |
; y |
pmax |
yp |
max |
y , |
p |
|
p |
|
|
p |
|
|
p |
|||
|
где yp |
tтабл |
myp . |
|
|
|
|
|
|
||
1.2Вопросы по главе
1.Что понимается под парной регрессией?
2.Какие задачи решаются при построении уравнения регрессии?
3.Какие методы применяются для выбора вида модели регрессии?
4.Какие функции чаще всего используются для построения уравнения парной регрессии?
5.Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?
6.По какой формуле вычисляется линейный коэффициент парной корреляции?
16
7.Как строится доверительный интервал для линейного коэффициента парной корреляции?
8.Как вычисляется индекс корреляции?
9.Как вычисляется и что показывает коэффициент детерминации?
10.Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
11.Для чего необходим критерий Фишера (F-критерий) в случаи парной регрессии?
12.Как строится доверительный интервал прогноза в случае линейной регрессии?
13.Как вычисляются и что показывают коэффициент эластичности, средний коэффициент эластичности?
1.3. Лабораторная работа № 1
На основе данных таблицы данных (см. Приложение) для соответствующего варианта :
1.Вычислить линейные коэффициенты парной корреляции для всех пар (x,y).
2.Выбрать два наибольших коэффициента корреляции и соответствующие пары экономических показателей (x,y).
3.Построить графики корреляционных полей (на основе точечной диаграммы).
4.Проверить значимость выбранных коэффициентов парной корреляции.
5.Построить доверительный интервал для линейного коэффициента парной корреляции.
Краткие указания к выполнению лабораторной работы с помощью программных средств MS Excel
1. Для расчета коэффициента линейной корреляции Пирсона необходимо использовать два способа:
А) Через встроенную функцию Коррел(), которая является стандартной для пакета MS Excel. Для этого, к исходной таблице данных добавляется новая
17
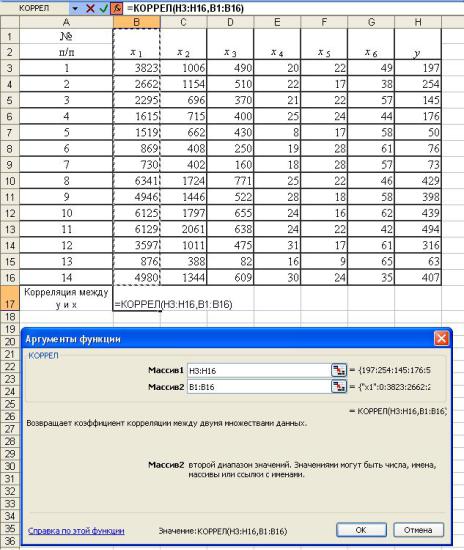
строка – "Корреляция между у и х", которая заполняется путем расчета значений корреляции между зависимой переменной y и соответствующей независимой переменной х. На рисунке 1.3 представлен пример расчета коэффциента корреляции между у и х1. Расчет проводится последовательно для всех пар (у, xi)
Б) При помощи пакета анализа данных MS Excel на основе расчета матрицы линейных корреляций Пирсона (см. Рис. 1.4). Для этого, в главном меню выбирается: Сервис Анализ данных Корреляция. В качестве входного интервала указывается весь диапазон данных исходной таблицы (Рис. 1.4). В полученной матрице корреляций рассматривается последняя строка, где указываются искомые значений корреляций между у и всеми независимыми переменными.
Рис. 1.3 Расчет коэффициентов корреляции между результативным признаком y и независимыми переменными x
18
Рис. 1.4. Расчет матрицы коэффициентов корреляции на основе пакета анализа данных MS Excel
2. Из полученного набора значений выбираются два наибольших и указываются те независимые переменные, которые наиболее сильно коррелированны с зависимой у.
3.Графики корреляционных полей строятся на основе точечной диаграммы, где в качестве оси абсцисс выбираются значения соответствующей негасимой переменной x, в качестве оси ординат – диапазон значений у (Рис. 1.5)
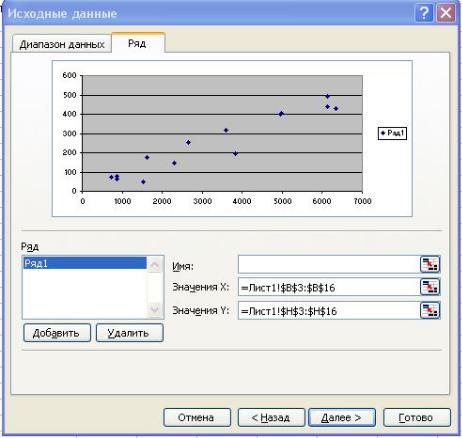 ).
).
Рис. 1.5. Использования точечной диаграммы для построения корреляционного поля
19

4. Проверка значимости коэффициентов корреляции проводится на основе t-критерия Стьюдента (см. п.1.1 теоретические основы этого раздела). А, именно, собственное распределение величины r (коэффициента корреляции) довольно сложное, поэтому необходимо применить преобразование:
При нулевой гипотезе о равентсве нулю коэффициента корреляции выборочное распределение статистики t есть распределение Стьюдента с n-2 степенями свободы. Если tфакт, полученное по формуле, указанной выше, меньше tтабл, тогда нулевая гипотеза принимается. Иначе нулевая гипотеза отвергается и принимается альтернативная гипотеза о неравенстве нулю коэффициента корреляции.
Для получения критических (или табличных) значений tтабл используется таблица
значений Стьюдента, приведенная в приложении для уровней значимости =0,05
и0,01.
5.Расчет доверительных интервалов для коэффициентов корреляции проводится по формулам указанным в данной главе. А именно:
1. Рассчитать фактическое значение z по следующей формуле:
1 1 r
zфакт 2 ln1 r
2. Рассчитать среднюю ошибку z:
mz |
|
|
1 |
|
|
|
|||
n 3 |
||||
|
|
|
3. Построить доверительный интервал для z, а именно:
zфакт tтабmz Z zфакт tтабmz
или
Zлевая Z Zправая
4. Левую и правую границу этого интервала преобразовать по формуле:
R |
|
|
e2Zлевая 1 |
;R |
|
e2Zправая 1 |
|
|
левая |
|
e2z 1 |
правая |
|
e2z 1 |
|
5. Окончательно, с вероятностью P=1- можно утверждать, что истинное значение коэффиицента корреляции будет лежать в пределах:
20
