
Основные определения и задачи статики
.pdf1.Основные определения и задачи статики.
Статика- раздел механики, в котором изучаются условия равновесия механической системы под действием сил.
Равновесие механической системы – такое состояние системы, при котором все ее точки под действием приложенных сил остается в покое относительно рассматриваемой системы отсчета.
Теоретическая механика изучает не реальные мат.тела, а их модели(матер.точка, мех.система, абсолютно твердое тело).
Материальная точка – точка, обладающая массой. Любая совокупность матер.точек – механическая система.
В механике матер.тело рассматривают как мех.систему, образованную непрерывной совокупностью матер.точек.
Матер.тело, в котором расстояние между двумя любыми точками всегда остается неизменным называют абсолютно твердым телом. Эти тела считаются сплошными.

2.Силы. Виды сил. Их классификация. Система сил.
Вприроде все тела взаимодействуют. Действие на данное матер.тело со стороны другого матер.тела, которое приводит к изменению скоростей точек этого тела или следствием которого явл-ся изменение относительного положения частей данного тела называют механическим воздействием
Мера механического воздействия одного матер.тела на другое называется силой.
Сила характеризуется точкой приложения и направлением действия. Она является векторной величиной. Когда тело находится в состоянии равновесия сила не производит реального действия, а лишь вызывает стремление тела к движению и измеряется по тому эффекту, какой бы она вызвала, если бы действовала при отсутствии любых препятствий.
Определяется числовым значением, точкой приложения и направлением.
Силу, как величину векторную, обозначают какой-либо буквой со знаком вектора, например,  или
или 
.
Имеются две меры действия: скалярная (численная) и векторная. За эталон численного значения силы принимают значение линейной силы упругости, например, пружинного динамометра, которая пропорциональна его деформации. Сила измеряется в ньютонах (Н), килоньютонах (кН).
Сила графически изображается в виде направленного отрезка.
Линией действия силы называется прямая, вдоль которой направлен вектор, изображающий силу.(Сила тяжести всегда направлена вертикально вниз)
Несколько сил, действующих на какое-то одно тело называется системой сил.
Силы, действующие на матер.точки твердого тела со стороны других точек этого же тела называются
внешними.
Система сил, линии действия которой лежат в одной плоскости , называется плоской системой сил.
Системой сил, эквивалентной нулю, (равновесной системой сил), называют такую систему сил, действие которой на твердое тело или материальную точку не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.
Равнодействующей силой рассматриваемой системы сил называют силу, действие которой на твердое тело или материальную точку эквивалентно действию этой системы сил.
Равновесная система сил имеет равнодействующую, равную нулю.
Уравновешивающей силой заданной системы сил считается такая сила, добавление которой к заданной дает новую систему, эквивалентную нулю.
Проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы

3.Аксиомы статики.
Аксиомы статики - основные положения, на которых основана теория равновесия, а именно они устанавливают основные свойства сил, приложенные к телу.
Аксиома1(принцип инерции) .Всякая изолированная материальная точка находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут ее из этого состояния.
Аксиома 2(условие равновесия двух сил). Если на свободное абсолютно твердое тело действует две силы, то тело может находиться в состоянии равновесия тогда, когда эти силы равны по модулю (F1=
F2) и направлены вдоль одной прямой в противоположные стороны (рис.1.4).
Аксиома 3(присоединения и исключения уравновешенных сил). Действие заданной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил.
Следствие: силу, приложенную к данному твердому телу можно переносить вдоль линии ее действия в любую ее точку. Действие силы на тело при этом не нарушится . Вектор силы F можно считать приложенным в любой точке на линии действия силы, следовательно вектор силы – скользящий
вектор
Аксиома 4 (аксиома параллелограмма сил). Две силы, приложенные в одной точке, имеют равнодействующую 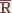 , приложенную в той же точке, которая является диагональю параллелограмма, построенного на этих силах, как на сторонах .
, приложенную в той же точке, которая является диагональю параллелограмма, построенного на этих силах, как на сторонах .
 .
.  (1.3)
(1.3)
Модуль равнодействующей  , как векторную сумму сил, вычисляют по формуле диагонали параллелограмма.
, как векторную сумму сил, вычисляют по формуле диагонали параллелограмма.
Опытная проверка правила сложения сил проводится следующим образом. Тело подвергается совместному действию нескольких тождественных, равно растянутых нитей. Далее на опыте исследуется, как располагаются все нити и значения сил (по показаниям динамометров) при равновесии .
Аксиома 5.(закон действия и противодействия) При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.
Если силы направлены к разным телам, то они не образуют уравновешенную систему.
Аксиома 6 (принцип отвердевания). Равновесие тела (системы тел) не нарушается от наложения на тело (систему тел) новых связей, если считать его абсолютно твердым телом.
С помощью этой аксиомы устанавливается, в частности, связь между условиями равновесия сил, приложенных к твердому и деформируемому телам. Иначе говоря, если система несущественно изменяет свою геометрию после нагружения, можно пользоваться условиями равновесия статики.
4.Связи и их реакции. Типы опор.
Свободным называют тело, не связанное с другими телами, которому из данного положения можно придать любое перемещение в пространстве.
Несвободное – тело, перемещению кот-го в пространстве препятствуют другие тела.
Тела, которые ограничивают перемещение данного тела, называют его связями.
Реакциями связи называют силы, действующие на материальные точки механической системы со стороны материальных тел, осуществляющих связи, наложенные на эту систему.
Активные силы сохраняются, если наложенные на систему связи мгновенно исчезнут.
Если силу, с которой тело действует на связь рассматривать как действие, то реакция мвязи приложена к телу будет противодействием.
Реакция связи направлена в сторону противоположную той. Куда связь не дает перемещаться телу.
Реакция связи зависит не только от вида связи, но и от характера движения системы.
При определении реакции связи используют принцип освобождения от связи: любое несвободное тело можно рассматривать как свободное, если условно освободить его от связи и заменить их действие на тело реакциями связи. И при этом в число сил, действующих на тело обязательно включаем реакции связи.
1.Свободное опирание тела о связь.
Гладкой поверхностью называют такие поверхности, если силой трения, возникающей в точках их контакта можно пренебречь.
Реакция R гладкой поверхности или опоры направлена по общей нормали к поверхностям иел в точке их касания и приложена в той же точке.
Если одна из соприкасающихся поверхностей является точкой, имеет заострение или ребро, то реакция направлена по нормали к другой поверхности.
2.Гибкая связь - это связь, с помощью гибкой нерастяжимой нити, которая не дает телу удаляться от точек подвеса нити. Поэтому реакция натянутой нити 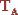 и направлена вдоль нити к точке их подвеса.
и направлена вдоль нити к точке их подвеса.

3.Стержневая связь – связь с помощью жесткого стержня. Концы которого закреплены шарнирно. Шарнир – подвижное соединение деталей, конструкций, допускающее вращение только вокруг общей оси или точки.
Реакции Ra,Rc направлены вдоль прямой, проходящей через центр концевых шарниров.
4.Шарнирно-подвижная опора - допускает перемещение балки (тела) в направлении, параллельном
опорной плоскости и поворот балки относительно опоры на угол . Перемещение, перпендикулярное опорной плоскости, отсутствует .
5.Шарнирно-неподвижная опора - допускает поворот балки (тела) относительно опоры и не допускает линейных перемещений.
6.Глухая заделка(жесткое защемление) – исключает любое перемещение тел, хар-ся реакцией и возникновением реактивного момента
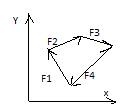
7.Сложение плоской системы сходящихся сил. Геометрическое условие равновесия ПССС.
Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке,
называются Плоской системой сходящихся сил.
Если силы ПССС приложены к разным точкам тела, то по первому следствию из аксиомы статики каждую силу можно перенести в точку пересечения линии действия и получить эквивалентную систему сил, приложенных в одной точке.
2 силы, приложенные к одной точке тела образуют простейшую ПССС
Ломаная линия, звенья которой равны и параллельны векторам заданных сил называется силовым
многоугольником.
Чтобы уравновесить систему сил достаточно добавить к ней еще одну силу, численно равную равнодействующей, но направленную в противоположную сторону.
В геометрической форме необходимое и достаточное условие ПССС:
Система сходящихся сил уравновешена только тогда, когда силовой треугольник замкнут.
8.Определение равнодействующей системы сходящихся сил методом проекций.
AE=F∑
Fx∑=F1x+F2x+F3x+F4x
Fy∑=F1y+F2y+F3y+F4y
Проекция равнодействующей системы сходящихся сил на каждую из осей координат равна алгебраической сумме проекций составляющих на эту ось.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы координат были равны 0.
9.Аналитическое условие равновесия ПССС
Вместо построения силового многоугольника равнодействующую системы более точно находят с помощью метода проекций(аналитически)
Проекцией вектора F на ось называется длина независимого отрезка оси, заключенного между двумя перпендикулярами, опущенных из начала и конца вектора F.
Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси.
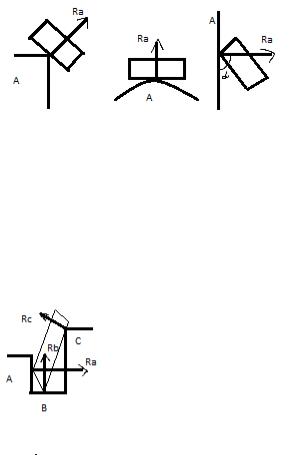
10.Определение усилий в стержнях фурмы по способу вырезания узлов.
Ферма - геометрическая стержневая система, у которой при расчете все узлы принимаются шарнирными.
Данный способ заключается в том, что мысленно вырезают узлы фермы, прикладывают к ним соответствующие внешние силы и реакции стержней и составляют уравнение равновесия сил, приложенных к каждому узлу.
Так как вначале расчета фермы не известно какие стержни сжаты, а какие растянуты, о условно принимают, что все стержни растянуты. Если в результате расчета получают ответ с минусом – стержень сжат.
Последовательность рассмотрения узлов определяется условием, что число неизвестных сил, приложенных к узлу не должно превышать числа уравнений равновесия сил.
Усилия в отдельных стержнях фермы могут оказаться равными нулю.
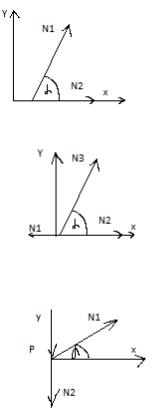
Ферма1. Если в ненагруженном узле плоской фермы сходится два стержня, то усилия в этих стержнях будут равны 0.
∑Xi = 0
N2+N1cosα = 0
N2=0
∑Yi=0
N1sinα=0
N1=0
Ферма2. Если в ненагруженном узле фермы сходится три стержня, из которых 2 расположены на одной прямой, то усилие в третьем стержне равно 0, а усилия в первых двух равны между собой.
∑Xi = 0
-N1+N2+N3cosα = 0
N2=N1
∑Yi=0
N3sinα=0
N3=0
Ферма3. Если в узле плоской фермы сходятся 2 стержня, и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилие в этом стержне равно по модулю приложенной силе, а усилие в другом стержне равно 0.
∑Xi = 0
N1cosα = 0
N1=0
∑Yi=0

-N2-Р=0
N2=-Р
11.Пара сил. Эквивалентность пар сил.
Система двух параллельных сил равных по величине и направленных в противоположные стороны называются парой сил.
Пара сил – неуравновешенная система и как следствие не имеет равнодействующей.
Пара сил на тело производит вращательное движение.
Вращательный эффект пары измеряется взятым со знаком+ илипроизведения модуля одной из сил пары на ее плечо(момент пары) M=±Fl
Знак + берется, если пара стремится повернуть тело против часовой стрелки.
В системе СИ момент силы измеряется в Н*м
Вращательное действие расположенной в плоскости пары зависит только от ее момента, и поэтому для задания пары сил достаточно указать числовое значение ее момента.
Теорема: Система пар, действующих на тело в одной плоскости эквивалентна паре сил с моментом равным алгебраической сумме моментов пар системы.
∑М = М1+М2+М3
12.Сложение пар сил. Условие равновесия пар.
Теорема: Система пар, действующих на тело в одной плоскости эквивалентна паре сил с моментом равным алгебраической сумме моментов пар системы.
∑М = М1+М2+М3
Если в результате сложения пар M=0, то эти действующие на тело пары сил образуют уравновешенную систему . Следовательно необходимое и достаточное условие равновесия пар сил: ∑Mi=0, т.е. для равновесия системы пар сил действующих на тело в одной плоскости необходимо и достаточно, чтобы алгебраическая сумма моментов была равна 0.
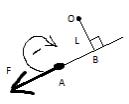
13.Момент силы относительно точки.
Моментом силы относительно точки называется взятое со знаком + или – произведение модуля силы на кратчайшее расстояние от точки до линии действия силы.
М(0)F=±Fl
Точка О, относительно которой берется момент силы называется центром момента(ОВ=l)
ОВ= l – кратчайшее расстояние от центра момента до линии действия силы называется плечом силы относительно данной точки.
