Основные формулы и теоремы.

1. Прямоугольный треугольник.

1. Теорема Пифагора а² + b² =с² .

2. Нахождение гипотенузы и катета

3. Катет есть среднее пропорциональное между гипотенузой ипроекцией этого катета на гипотенузу: а =

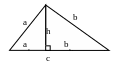
Теорема позволяет

а) зная проекцию катета и гипотенузу, найти катет;

б) зная катет и гипотенузу, найти проекцию катета,

в) зная катет и его проекцию, найти гипотенузу.

4. Высота есть среднее пропорциональное между проекциями катетов на гипотенузу: или

Теорема позволяет:

а) зная проекции катетов, найти высоту;

б) зная проекции катетов, найти площадь;

в) построить среднее пропорциональное двух отрезков

5. — высота, опущенная на гипотенузу.

6. — радиус описанной окружности.

7. Центр описанной окружности лежит на середине гипотенузы.

8. Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.

9. — радиус вписанной окружности.

10. Катет, лежащий против угла в 30°, равен половине гипотенузы.

11. Сумма острых углов прямоугольного треугольника равна 90⁰.

12. Признаки равенства прямоугольных треугольников:

а) по двум катетам;

б) по гипотенузе и прилежащему катету;

в) по гипотенузе и противолежащему катету;

г) по гипотенузе и острому углу.

1

В

3. Соотношения между сторонами и углами в прямоугольном треугольнике:

— отношение прилежащего катета к гипотенузе

α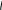

— отношение противолежащего катета к гипотенузе

A

С

— отношение противолежащего катета к прилежащему

— отношение прилежащего катета к прилежащему

Из определения sinα, cosα, tgα получаем следующие правила:

1. Катет противолежащий углу α равен произведению гипотенузы на sinα: ВС=АВ∙ sinα.

2. Катет прилежащий углу α равен произведению гипотенузы на cosα: AС=АВ∙ cosα.

3. Катет противолежащий углу α равен произведению второго катета на tgα: ВС=АС∙ tgα.

2. Правильный треугольник.

— площадь или ( )

— высота (биссектриса, медиана)

- сторона через радиус описанной окружности

— радиус описанной окружности через сторону

- радиус вписанной окружности

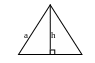
3. Треугольник.

1. Признаки равенства треугольников:

а) по двум сторонам и углу между ними;

б) по стороне и прилежащим к ней углам;

в) по трем сторонам.

2. Теорема косинусов: . (Рис 4.)

Теорема позволяет:

а) найти сторону треугольника по двум другим сторонам и углу между ними;

б) зная три стороны, найти угол (косинус угла): ,

в) по двум сторонам и углу напротив одной из них найти третью сторону (задача может иметь два решения).

Следствия.

Если , где с - наибольшая сторона треугольника, то данный треугольник - тупоугольный , если - прямоугольный, если - остроугольный .

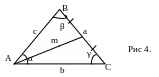
3. Теорема синусов: (Рис 4.)

Теорема позволяет:

а) зная две стороны и угол напротив одной из них, найти угол (синус угла) напротив второй стороны;

б) зная два угла и одну из сторон, найти остальные стороны;

а) по стороне и противолежащему углу найти радиус описанной окружности;

г) по радиусу описанной окружности и стороне треугольника найти угол, лежащий напротив данной стороны (может иметь два решения в силу справедливости формулы sin α = sin (180° - α));

д) по радиусу описанной окружности и углу при вершине треугольника найти основание треугольника.

4. Свойство медиан треугольника:

а) Медианы треугольника пересекаются в одной точке и делятся ей в отношении 2:1, считая от вершины.

б) Медиана делит треугольник на 2 равновеликих треугольника (равновеликие — это значит равные площади).

в) Три медианы делят треугольник на 6 равновеликих треугольников.

г) Формула медианы: (Рис 4.)

5. Свойство биссектрисы треугольника:

Биссектриса треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам треугольника, т.е. , или .

6. Биссектрисы внутреннего и внешнего углов при одной вершине треугольника взаимно перпендикулярны.

7. Формулы биссектрисы: или

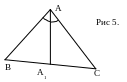
8. Высоты треугольника обратно пропорциональны его сторонам, т.е. , откуда (Рис 5.).

9. Нахождение высоты треугольника:

10. Отрезок, соединяющий основания двух высот треугольника отсекает треугольник, подобный данному.

11. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третей стороне и равна её половине.

MN║AC и .(Рис 6.)

В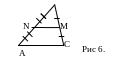

12. Признаки подобия треугольников: а) По двум углам.

б) По двум сторонам и углу между ними.

в) По трем сторонам.

13. Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

Теорема. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

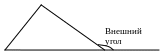
14. Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона — основанием.

Свойство равнобедренного треугольника: В равнобедренном треугольнике углы при основании равны.

Признак равнобедренного треугольника: Если в треугольнике два угла равны, то он равнобедренный.

15. Высотой треугольника, опущенной из данной вершины называется перпендикуляр, проведенный из этой вешины к прямой, которая содержит противолежащую сторону треугольника.(Рис 7а., 7б.)

16. Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вешину с серединой противолежащую стороны треугольника.(Рис 7 в.)

17. Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вешину с точкой на противолежащей стороне. (Рис 7 г.)

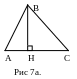
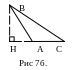
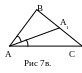
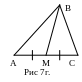
18. Свойство медианы равнобедренного треугольника: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

19. Неравенство треугольника: Каков бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.

20. Теорема об изменении синуса, косинуса и тангенса при возрастании угла: При возрастании острого угла sinα и tgα возрастают, а cosα убывает.

21. В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.