22. Модуль.

a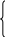 , если a≥0

Определение

-a, если a<0

РАСКРЫТИЕ МОДУЛЯ ПО ОПРЕДЕЛЕНИЮ

Пример. |х-2|

Если х-2 ≥0, т.е.х≥2,то |х-2|= х-2.

Если х - 2 < 0, т.е. х<2, то |х-2|= -(х-2) = 2-х.

ОСНОВНЫЕ СВОЙСТВА МОДУЛЯ

1. |а|≥0 3. |ab|= |a|∙|b|

2. |а-b|=|b-а| 4. |а-b|²=(а-b)².

Геометрический смысл модуля

|а|— это расстояние от точки А(а) до начала отсчета.

|а-b| — это расстояние между точками А(а) и В(b).

УРАВНЕНИЯ С МОДУЛЕМ.

1. |x|=а.

а) если а ≥0, то х = а или х = - а

б) если а < 0, то корней нет.

2. |x-b|=а.

а) если а ≥0,то х-b = а или х - b = - а, (решаем каждое уравнение),

б) если а < 0, то корней нет.

3. |f(x)|= |g(x)|.

f(x) = g(x) или f(x) = -g(x).

4. |f(x)|= g(x).

f(x) = g(x) и g(x) ≥ 0 или

f(x) = -g(x) и g(x)≥0.

НЕРАВЕНСТВА С МОДУЛЕМ

1. |f(x)| <a

а) если a ≥ 0, то - a < f(x) < a.

б) если а < 0, то решений нет

Пример. |2x-3|<5.

-5<2x-3<5, -2<2x<8, -1<x<4.

2. |f(x)|≥a

а) если а > 0, то f(x) ≥ а или f(x) ≤ - а

б) если а ≤ 0, то х R.

Пример. |x+1|>2.

x+l>2 или x + 1<-2

х>1 х<-3

Ответ:

3. |f(x)|<g(x)

- g(x)<f(x)<g(x)

4 . |f(x)|>g(x) f(x)> g(x) или f(x)<-g(x)

Неравенства |f(x)|> |g(x)|и f(x)²> g(x)² равносильны.

23. Иррациональные уравнения.

Пример 1. Пример 2.

2x +1 = 9 корней нет

x= 4

У равнение равносильно системе:

У равнение равносильно системе:

Неравенство в системе, обычно, проверяют, а не решают.

24. Прогрессии.

Арифметическая прогрессия: (а_n), а_n=a_n-1+d, где d— разность арифметической прогрессии,

а_n=a₁+(n-1)d.

Формулы суммы n первых членов прогрессии , .

Свойство: …..,а_n-1, a_n, a_n+1,….., тогда .

Геометрическая прогрессия: (b_n), b_n=b₁∙q^n-1, где q — знаменатель Г.П.

Формулы суммы n первых членов прогрессии: , , q 1.

Свойство: …..,b_n-1, b_n, b_n+1,…..,

Пусть (b_n) ─ бесконечная убывающая геометрическая прогрессия, тогда сумму этой прогрессии находят по формуле: S= , где .