4.6. Связь между планами двойственных задач
Рассмотрим симметричную пару двойственных задач:
|
f(x) = < c, x > max; |
(4.4) |
g(y) = < b, y > min; |
(4.7) |
|
Ax b; |
(4.5) |
ATy c; |
(4.8) |
|
x 0 |
(4.6) |
y 0 |
(4.9) |
|
x = (x1,…,xn ). |
|
y = (y1,…,ym ). |
|
Между решениями этих задач существует тесная связь, отражаемая следующими свойствами и теоремами.
Свойство 1. Основное неравенство теории двойственности. Для любых допустимых планов x (прямой задачи) и y (двойственной задачи) выполняется неравенство
|
f(x) g(y) или < c , x > < b , y > . |
(4.10) |
Доказательство.
Неравенство Ax b умножим скалярно на y 0. Получим
|
< Ax, y> < b, y> . |
(4.11) |
Умножая неравенство ATy c скалярно на x 0 , получим
|
< AT y, x> < c, x>. |
(4.12) |
Воспользуемся известным правилом перекидки матрицы в скалярном произведении.
< Ax, y> = < x, AT y> .
Применяя его к левой части (4.11), придем к неравенству
|
< x, AT y> < b, y> . |
(4.13) |
Левые части неравенств (4.12) и (4.13) равны. Следовательно, можем записать цепочку отношений
< c, x > < AT y , x> = < x, AT y> < b, y> ,
из которой получаем требуемое неравенство.
Свойство 2. Достаточное условие оптимальности планов двойственных задач. Пусть x*, y* – некоторые допустимые планы прямой и двойственной задач соответственно, причем
|
< c , x*> = < b , y*> . |
(4.14) |
Тогда x* – оптимальный план задачи (4.4) – (4.6), y* – оптимальный план задачи (4.7) – (4.9).
Доказательство.
Пусть x – любой допустимый план задачи (4.4)–(4.6), аy*– план двойственной задачи, удовлетворяющий условию (4.14). По свойству 1:
< c , x > < b , y* > = < c , x* >,
следовательно
< c , x* > < c , x > для всех x X ,
а это означает, что x* – оптимальный план в задаче (4.4) – (4.6).
Пусть теперь y – допустимый план двойственной задачи, x* – план исходной задачи, удовлетворяющий условию (4.14). По свойству 1:
< b , y > < c, x* > = < b , y * > ,
следовательно
< b , y* > < b , y > для всех y Y,
а это и говорит о том, что y* – оптимальный план в задаче (4)–(6).
4.7. Первая теорема двойственности
Кроме основного неравенства и достаточного признака оптимальности планов взаимно двойственных задач существуют и другие связи между их решениями. Важно установить, влияет ли наличие или отсутствие решения одной из пары задач на существование решения в другой. Ответ на этот вопрос дает следующая теорема, известная как первая теорема двойственности.
Теорема 1. Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план, причем значения целевых функций на этих планах равны
f(x*) = g(x*) или < c , x*> = < b , y*> .
Если же целевая функция одной из пары двойственных задач не ограничена на своём множестве планов (прямая – сверху, двойственная – снизу), то множество планов другой задачи пусто.
Из первой части теоремы, которую мы приводим без доказательства, следует, что равенство (4.14) является не только достаточным, но и необходимым условием оптимальности планов пары двойственных задач.
Утверждение второй части теоремы легко доказывается от противного. Предположим, что в прямой задаче (4.4)-(4.6) целевая функция не ограничена сверху на множестве X , то есть max f(x) , x X , но множество планов Y двойственной задачи не пусто – существует хотя бы одна точка y Y . Тогда в силу основного неравенства теории двойственности max f(x) g(y), что противоречит неограниченности целевой функции прямой задачи. Таким образом, неограниченность сверху целевой функции исходной задачи влечет за собой несовместность ограничений двойственной задачи. Аналогично доказывается, что из неограниченности снизу двойственной целевой функции g(y) на множестве Y, следует пустота множества планов X прямой задачи.
Интересно, что обратное утверждение не верно. Из пустоты множества планов одной задачи еще не следует неограниченность целевой функции в двойственной к ней задаче. (Оба множества могут быть пусты).
Первая теорема двойственности позволяет исследовать любой заданный план на оптимальность
Пример. Проверить, является ли точка x/= (0.5, 0, 0) оптимальным планом задачи ЛП.
f(x) = 4x1+4x2+4x3 max,
2x1+x2+2x3 2;
4x1+2x2+x3 2;
x1, x2, x3 0.
Решение.
Во-первых, проверим, принадлежит ли точка x/ множеству допустимых планов X. Для этого подставим x/= (0.5, 0, 0) в ограничения. Получим:
2·0.5+1·0+2·0 < 2,
4·0.5+2·0+1·0 = 2.
Следовательно, x/= (0.5, 0, 0) удовлетворяет ограничениям, то есть принадлежит множеству допустимых планов X.
Построим для этой задачи двойственную задачу линейного программирования:
g(y) = 2y1+2y2 min;
2y1+4y2 4;
1y1+2y2 4;
2y1+1y2 4;
y1 , y2 0.
Теперь решим эту задачу графически. Построим граничные прямые
P1 : 2y1+4y2 = 4 проходит через точки: (0, 1); (2, 0);
P2 : y1+2y2 = 4 проходит через точки: (0, 2); (4, 0) ;
P3 : 2y1+y2 = 4 проходит через точки: (0, 4); (2, 0) ;
и выделим множество планов двойственной задачи.
Целевой вектор (2, 2) совпадает с биссектрисой первого координатного угла.
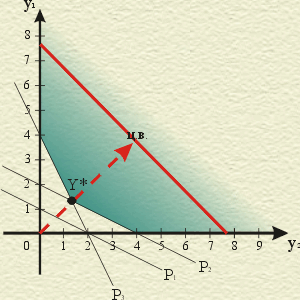
Оптимальный план двойственной задачи y* лежит на пересечение прямых P2 и P3. Решая систему из уравнений, описывающих эти прямые,
y1*+2y2* = 4,
2y1*+y2* = 4,
получаем:
y* = (4/3; 4/3).
Подсчитаем значение функции g(y*) в этой точке. Оно равно
g(y*) = 8/3+8/3 = 16/3.
Следовательно, для того, чтобы план x / был оптимальным, значение функции f(x /) должно быть равно 16/3. Проверяем это:
f(x/) = 2 < g(y*) =16/3.
Можно с уверенностью сказать, что x / – не оптимальный план!
Проверим план x// = (0; 2/3; 2/3) X: f(x//) = 16/3, f(x//) = g(y*), следовательно, x// – оптимальный план.
В силу того, что каноническая задача ЛП сводится к стандартной, все соотношения, доказанные для симметричной пары двойственных задач, справедливы и для несимметричной пары и наоборот.