Глава 4

Двойственность в линейном программировании

4.1. Двойственные задачи линейного

программирования

С любой задачей ЛП можно связать некоторую другую задачу ЛП, которая по отношению к первой  называется двойственной. Тогда исходная задача будет называться прямой.

Рассмотрим стандартную задачу ЛП с n переменными и m ограничениями в форме неравенств

f(x) = c₁ x₁ + c₂ x₂ + …+ c_n x_nmax;

a₁₁ x₁ + a₁₂ x₂ + … + a_1n x_n  b₁ ;

a₂₁ x₁ + a₂₂ x₂ + … + a_2n x_n   b₂ ;

………………………………........……

a_m1 x₁ + a_m2 x₂ + … + a_mn x_n  b_m ;

x_j0,   j = 1, 2, …, n .

Двойственной к ней называется задача ЛП  следующего вида 

g(y) = b₁ y₁+ b₂ y₂  + …+ b_m y_mmin;

a₁₁ y₁ + a₂₁ y₂ + … + a_m1 y_m   c₁;

a₁₂ y₁ + a₂₂ y₂ + … + a_m2 y_m   c₂;

................................………………

a_1n y₁ + a_2n y₂ + … + a_mn y_m   c_n;

y_i  0,   i = 1, 2, …, m .

Выписывая матрицы условий  для прямой и двойственной задачи

, ,

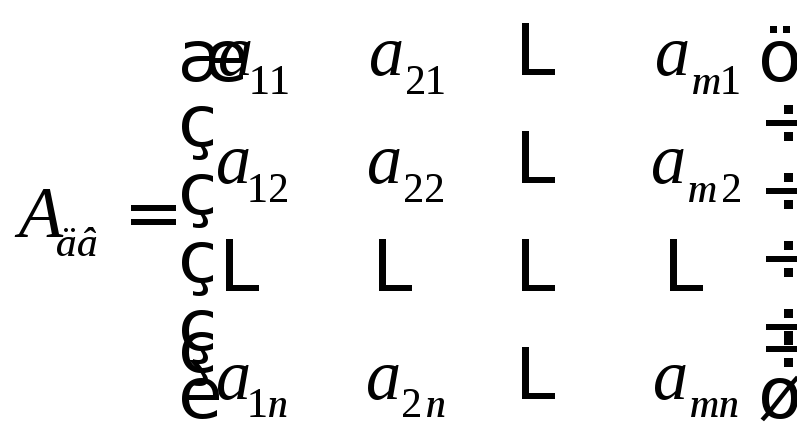видим, что   А_дв = А^T_пр .

Следовательно, пара двойственных задач  может быть записана в матричной форме:

 

Прямая задача ЛП	Двойственная задача ЛП
f(x) = < c, x >  max; Ax  b;  x  0.	g(y) = < b, y >  min; ATy  с;  y   .

 

4.2. Симметричная пара двойственных задач

Пара двойственных задач, в которых прямая задача – стандартная, называется симметричной парой двойственных задач.

Правила построения двойственной задачи к стандартной задаче ЛП.

1. Число переменных двойственной задачи равно числу основных ограничений прямой задачи и наоборот.

2. Если прямая задача есть задача на  max  при ограничениях  “”, то двойственная задача – задача на  min  при ограничениях  “”.

3. Правые части ограничений прямой задачи – числа  b_i – становятся коэффициентами целевой функции двойственной задачи.

4. Коэффициенты целевой функции прямой задачи – числа  c_j – становятся правыми частями ограничений двойственной задачи ЛП.

5. j–й столбец матрицы условий прямой задачи превращается в  j–ю строку матрицы условий двойственной задачи.

6. Переменные прямой и двойственной задачи неотрицательны.

Пример. Рассмотрим стандартную задачу ЛП с двумя переменными, тремя ограничениями в форме неравенств и условиями неотрицательности:

f(x)=2x₁ – 4x₂  max;

x₁ + 3x₂   8;

–3x₁+ x₂  –7;

2x₁ – 5x₂ 10;

x₁, x₂  0.

Построим к ней двойственную задачу, руководствуясь правилами. Она будет иметь три переменных и два ограничения:

g(y)=8 y₁ – 7y₂+10 y₃  min;

y₁ – 3 y₂+ 2 y₃  2;

3y₁+ y₂ –5 y₃ – 4;

y₁, y₂   0.

Покажем, что двойственная к двойственной задаче ЛП совпадает с прямой задачей ЛП, для чего воспользуемся предыдущим примером.

Сначала приведем двойственную задачу к стандартному виду

g(y)= – 8y₁ + 7y₂ –10 y₃  max;

y₁+ 3y₂ – 2y₃ –2;

– 3y₁ – y₂+ 5y₃ 4;

y₁, y₂  0.

Построим к ней двойственную задачу по правилам 1-6, обозначая двойственные переменные через x₁ , x₂ . 

f(x)= – 2x₁+ 4 x₂  min;

– x₁ – 3x₂   –8;

3x₁ – x₂  7;

– 2x₁+ 5x₂  –10;

x₁, x₂ 0.

Чтобы получить исходную задачу,  достаточно умножить коэффициенты целевой функции и все ограничения на (–1).

 Из вышесказанного следует, что, если прямая задача имеет вид:

f(x) = < c, x >  min;

Ax b,    x  0,

то двойственной к ней будет  задача

g(y) = < b, y >  max;

A^Ty   с ,   y  0.