2013.Термодинамика / Paskal / 2011_09_27 / 2011_09_27 / IMG_0027-70-71

- 70 -

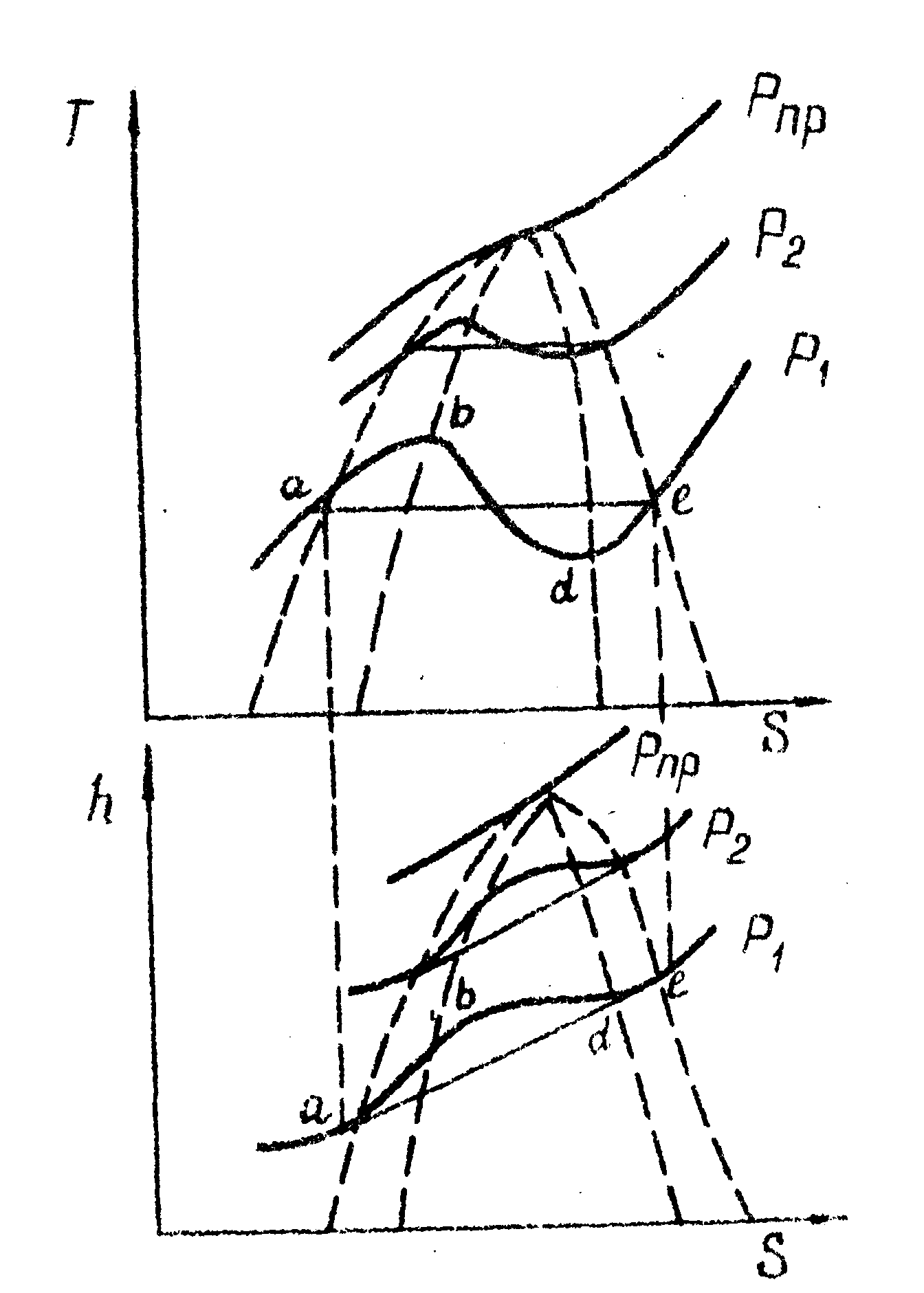
жащая куполообразные бинодаль и спинодаль (рис.1-30). Таким образом_;весь анализ, проведенный в §5 на основе изотермы Ван-дер-Ваальса, мог бы быть проведён и на основе изобары.

Рис. 1-29. Семейства изобар

й ; для системы жидкость-газ

Внутренняя энер­гия системы Ваи-лео-Яаальса.

Ради полноты описания модели Ван-дер-Ваальса пределим соответствующую ей внутреннюю энер гию. Для этого в_,подставим (1.6.5). Тогда

Проинтегрировав это выражение, получим

(1.6.11) (.легко показать, что константа интегрирования равна нулю), где В выражении (1.6.11) представляет кинетическую, а - - потенциальную энергию.

Достижимость не­устойчивых одно-фазттых состояний

Как и в §5, примем пока, что лабильнее однофазное состояние, предсказываемое моделью Ван-дер-Ваальса, существует. Каким образом оно может быть в

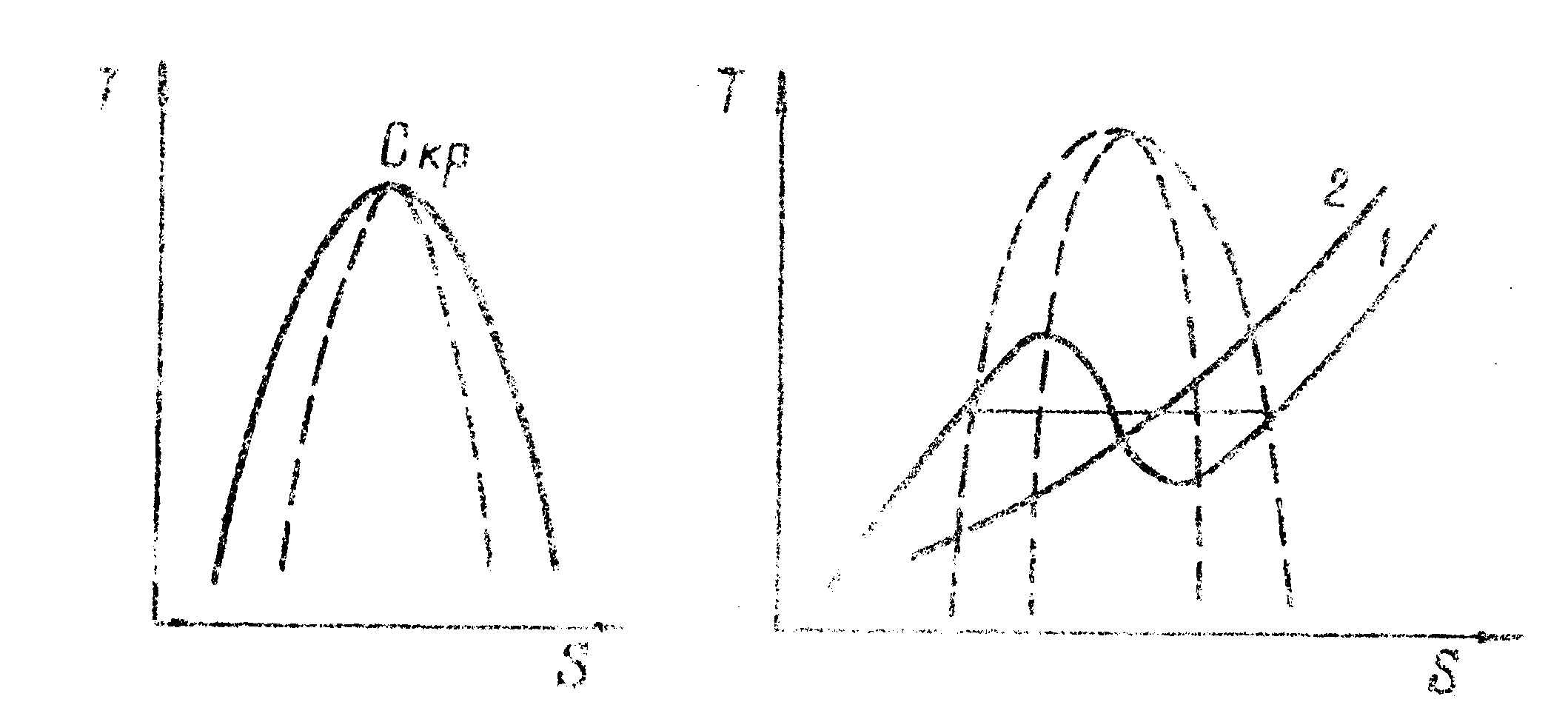
Рис. 1-30. Диаграмма состояния Т –S для cистемы жид кость-газ

Рис, 1–31. Изобарный и изохорный переходы в системе жидкость-газ (1–изобара. 2 – изохора)

принципе реализовано, достигнуто? Очевидно, что лабильное состояние принципиально недостижимо ни изотермическим ни изобарным способом. Исключение составляют крайние точки и изотермы и изобары, соответствующее пределам устойчивости (метастабильности). Однако лабильные состояния в принципе могут быть постигнуты(помимо точек и) изохорным или изэнтропическим путём. Изохорный процесс удобно проследить на изобарическом графике (рис. 1-31).

Поскольку всегда, система Ван-дер-Ваальса изохорно всегда устойчива.. Снижая или повышая изохорным образом температуру, можно ввести в систему состояние, соответствующее лабильному участку изобары или изотермы, изменение температуры должно быть произведено настолько быстро, чтобы при этом не успело пройти разрушение лабильного состояния. В случае системы жидкость-газ невозможно осуществить столь быстрое охлаждение (но закалка на. лабильное или, точнее, на близкое к лабильному состоянию возможна в кристаллических системах с подобным поведением). Заметим, что постояно положительной наклон изохоры об-