Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

attachments_26-06-2014_11-15-27 / Лекц 28 Пар 20 Мет Функ ГРИНА

.pdf

Скачиваний:

Добавлен:

30.05.2015

Размер:

388.32 Кб

Скачать

☆

§20. Метод функций Грина

Мы можем переписать формулы (161), (162) в общем виде

					u
u x En x y u y dy		u y		En x y En x y	dS y	(163)
u x En x y u y dy		u y	n	En x y En x y	dS y	(163)
G	G		n		n

где En x − фундаментальное решение оператора Лапласа, действующего на функции с n независимыми переменными (см. формулы (133) и (134)).

Рассмотрим теперь такую краевую задачу (называемую задачей Дирихле):

u x f x ,

u G u0 x .

С помощью формулы (163) получаем

u x En x y f y dy			y		En x y En x y	u
		u0				dS y
				n
G	G					n

(164)

(165)

Можем сказать, что функция, заданная формулой (165) является решением задачи Дирихле (164).

Формулой (165) пользоваться, однако, затруднительно, так как в поста-

новке задачи (164) не указано явно поведение производной на границе G .

Идея метода функций Грина состоит в том, чтобы заменить функцию En x y на некоторую другую функцию x, y En x y g x, y , называемую функцией Грина. При этом g x, y подбирается таким образом, чтобы в аналоге

формулы (165) исчез интеграл, содержащий производную nu .

Определение 20.1. Функцией Грина для оператора Лапласа называется функция x, y двух переменных x, y G , где G n − ограниченная область, если выполнены условия:

1.x, y является гармонической функцией в области G \ y по перемен-

ной x и x x, y x y ;

2.x, y x G 0;

3.Γ x, y En x y g x, y , где En x − фундаментальное решение оператора Лапласа и g x, y − регулярная и гармоническая функция по пе-

ременной x , т.е. x g x, y 0 .

Предложение 20.2. Кроме перечисленных свойств, для функции Грина автоматически выполняется также следующее свойство:

4. x, y y, x .

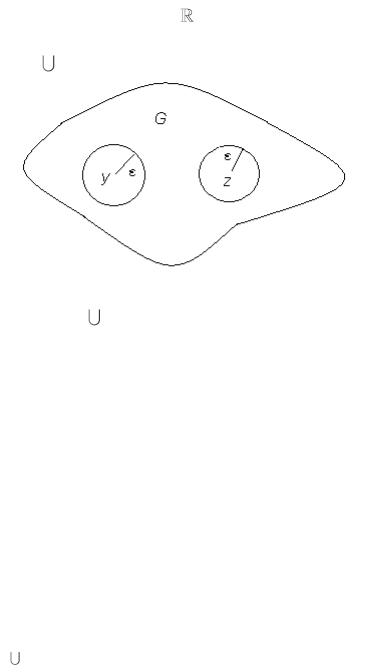
Доказательство. (Б/Д) Пусть G n − область. Возьмем точки y и z в

этой области и окружим эти точки шарами радиуса 0 . Выбираем настоль-
ко малым, что U y,	U z, G .

Обозначим G G \
	U z,	U y,	и воспользуемся формулой Грина:
	v u u v dx				u	u	v
				v	n			dS .	(Г3)

G			G				n

Вэтой формуле положим u x x, z и v x x, y . Заметим, что

x x, y 0 и x x, z 0 согласно свойству 1 функции Грина. Следова-

тельно, левая часть формулы (Г3) равна нулю. По свойству 2 x, y

x G 0 и

x, z

x G 0 . Поэтому в правой части формулы (Г3) остается только инте-

грал по границам окрестностей U y,

и U z, в точках y и z , т.е. по сферам

S y и S z . Суммируя сказанное, мы приходим к формуле

Γ x, z

Γ x, y

Γ x, z

dSx 0

S y S z

из которой следует равенство (*):

Γ x, z

Γ x, y

Γ x, z

Γ x, y

Γ x, z

dSx Γ x, z

x, y

dSx

S y

S z

Найдем предел левой части при 0 . По свойству 3

Γ x, y En x y g x, y , подставим вместо x, y это выражение. Заметим,

что lim

g x, y

Γ x, z

dSx 0 , так как по условию g x, y является гар-

S y

Γ x, z

монической и потому непрерывной функцией, а функция непрерывна

во всех точка шара U y, . Кроме того, т.к. непрерывная функция на компакте

ограничена, то существует константа C такая, что	x, z	C .
	x, z


	n
	n

Следовательно (ограничиваемся случаем n 3 , иные размерности рассматриваются аналогично),

En x y

Γ x, z

dSx

0 .

x y

S y

x y

В левой части формулы (*) первый интеграл стремится к нулю:

Γ x, y

Γ x, z

dSx 0

при 0 ,

S y

рассмотрим второй интеграл. Имеем

Γ x, z

Γ x, y

Γ x, z

g x, y

dSx

x y

S y

x y

Γ x, z

dSx

Γ x, z g dSx .

x y

Так как функция непрерывна, а функция g − гармоническая (следовательно,

имеет непрерывную производную

g ), то второй интеграл в последнем выра-

жении будут стремиться к нулю при 0 . Далее заметим, что

, где вектор n

− нормаль, направлен-

x y

ная внутрь шара по радиусу r

x y

к его центру. Следовательно,

Γ x, z

dSx

Γ x, z dSx .

x y

4 2

x y

Так как функция x, z на сфере

x y

непрерывна, то можно воспользо-

ваться теоремой о среднем:

Γ x, z dSx

4 2

x, z 4

Γ x, z ,

x y

где xˆ − некоторая точка на сфере x y . Тогда

Γxˆ, z Γ y, z при 0 .

Витоге левая часть формулы (*) при 0 стремится к Γ y, z . Аналогично доказывается, что правая часть этой формулы при 0 стремится к Γ z, y .

■

Теорема 20.3. Пусть G n − ограниченная область, f x C G и

u0 x C G . Тогда решение задачи Дирихле (164) может быть найдено по формуле:

u x Γ x, y f y dy

u0 y

Γ x, y

dS y ,

(166)

где Γ x, y

− функция Грина для оператора Лапласа.

Доказательство. Из пунктов 2 и 3 определения 20.1 следует, что

g x, y

x G En x y

x G

(**)

По формуле Грина (Г3) при v g , u f , получаем:

0 g x, y f x dx

x, y

dSx .

(***)

В формулах (163) и (***) отдельно сложим правые части и левые. Тогда

u x

g x, y E

x y

f y

En x y

g x, y

E x y dS.

Но последний интеграл в этой формуле равен 0 ввиду формулы (**).

■

Замечание 20.4. Построение функции Грина сводится к решению задачи

g x, y 0,

(167)

g x, y |

E x y |

, x G.

y G n

y G

Теорема 20.5. Если функция Грина существует, то она единственна.

Доказательство. Допустим, что в области G существуют две функции Грина:

Γ1 x, y En x y g1 x, y , Γ2 x, y En x y g2 x, y .

Тогда их разность g1 x, y g2 x, y будет функцией, гармонической внутри

области G и непрерывной на еѐ замыкании G

, причем на границе G

эта

функция тождественно равна 0. По следствию 19.5,

g1 x, y g2 x, y 0 всю-

ду в области G . Отсюда сразу получаем, что Γ1 x, y Γ2 x, y .

■

Теорема 20.6. Функция Грина для области G является неположительной

во всех еѐ точках.

Доказательство. Нам известно, что функция En x y

стремится к

при y x (например, при n 3 E

x y

). Функция g x, y −

x y

гармоническая, в частности, непрерывная функция. Следовательно,

при y x . Для точки x G найдется сфера

x, y

y G;

y x

до-

статочно малого радиуса, на которой Γ x, y C , где C 0 . По свойству 2

функции Грина Γ x, y 0 на границе G . Функция Γ x, y является гармонической в области G \ y; y x как разность двух гармонических функций,

значит для нее выполнен принцип максимума (минимума). Следовательно, функция Γ x, y принимает неположительные значения во всех точках области

G \ y; y x . Устремляя к нулю, приходим к нужному заключению. ■

Соседние файлы в папке attachments_26-06-2014_11-15-27

#
30.05.2015255.46 Кб13Лекц 23 Пар 17 Св-ва Ф Р продолж.pdf
#
30.05.2015274.02 Кб31Лекц 24 Пар 18 Обобщ Задача Коши.pdf
#
30.05.2015303 Кб18Лекц 25 Пар 18 продолж.pdf
#
30.05.2015295.42 Кб17Лекц 26 Пар 18 ПРОпродолж.pdf
#
30.05.2015262.69 Кб15Лекц 27 Пар 19 ГАРМонич функции.pdf
#
30.05.2015388.32 Кб13Лекц 28 Пар 20 Мет Функ ГРИНА.pdf
#
30.05.2015511.69 Кб14Лекц 29 Пар 20 продолж.pdf
#
30.05.2015230.03 Кб15Лекц 30 Пар 21 Кр Задачи ЛАП ПУАС.pdf
#
30.05.2015249.34 Кб14Лекц 31 Пар 22 Прос СОБ и нер ФРИДР.pdf
#
30.05.2015237.13 Кб16Лекц 32 Пар 23 СЛЕД.pdf
#
30.05.2015226.36 Кб16Лекц 33 Пар 24 Теор СУЩ Дирихле.pdf