§5. Определённый интеграл с переменным верхним пределом. Существование первообразной функции. Формула Ньютона-Лейбница.
Пусть f
R[a;b].
Тогда x:
a≤x≤b
f
R[a;x],
т.е. существует
.
Переменную интегрирования обозначим
черезt,
чтобы не смешивать её с верхним пределом
x.
Это можно сделать, т.к. величина
определённого интеграла не зависит от
буквенного обозначения переменной
интегрирования. Рассмотрим функцию
Ф(х)
, (1)
определённую на [a;b]. Она называется интегралом с переменным верхним пределом.
Теорема 1. Если f(x) непрерывна на [a;b], то функция Ф(x) имеет производную в каждой точке x[a;b], причём Ф (x)=f(x). (2)
Доказательство.
Выберем произвольно
точку x0
[a;b].
Точке x0
придадим приращение Δx≠0
так, чтобы x0+Δx
[a;b].
Тогда Ф(x)
получит приращение
ΔФ(x0)=Ф(x0+Δx)-Ф(x0)=
,
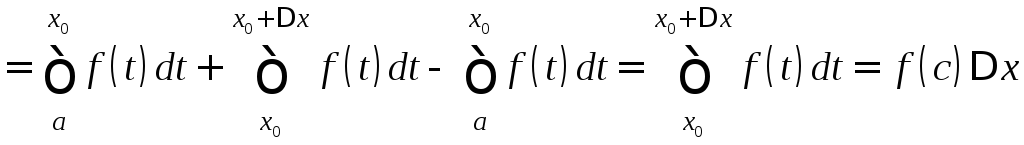где c
[x0;x0+Δx]
(по теореме о среднем). При Δx→0
c→x0.
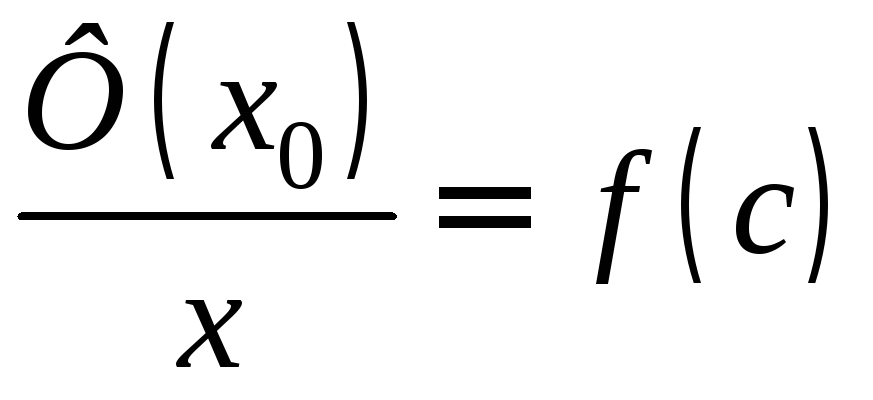. (3)
По условию f
непрерывна в точке x0
(т.к. f
C[a;b]).
Следовательно, существует
.
Т.к. существует предел правой части равенства (3), равный f(x0), то существует и предел левой части равный Ф (x0). Переходя в равенстве (3) к пределу, получим Ф (x0)=f(x0).
Итак, если f
C[a;b],
то Ф
имеет производную в каждой точке
x[a;b],
и при этом Ф
(x)=f(x).
Теорема 2. Если
f
C[a;b],
то она на [a;b]
имеет первообразную, причём любая её
первообразная имеет вид
.
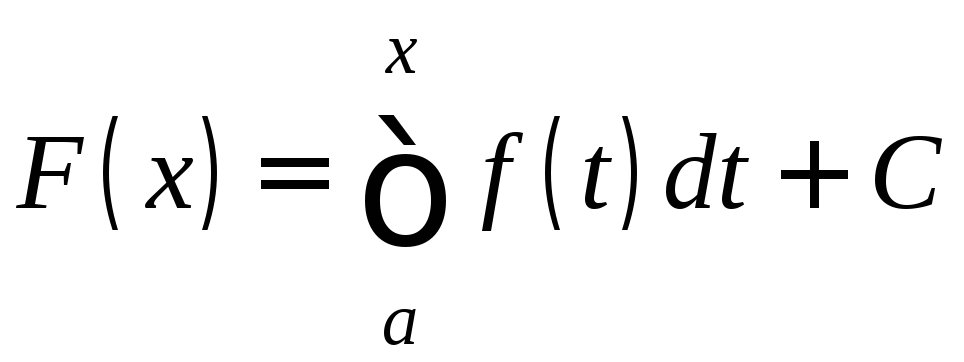Доказательство.
Т.к. f
C[a;b],
то по теореме 1 Ф(x)
дифференцируема на [a;b]
и Ф
(x)=f(x),
т.е. Ф(x)
является первообразной для f(x)
на [a;b].
Следовательно, любая первообразная
F(x)
на [a;b]
будет иметь вид F(x)=Ф(x)+C
или
.
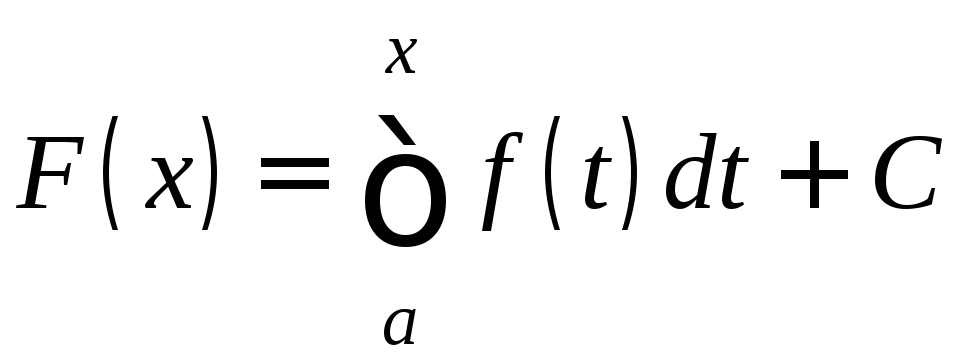Теорема 3. Пусть
f
непрерывна на [a;b].
Если F(x)
является произвольной её первообразной
на [a;b],
то
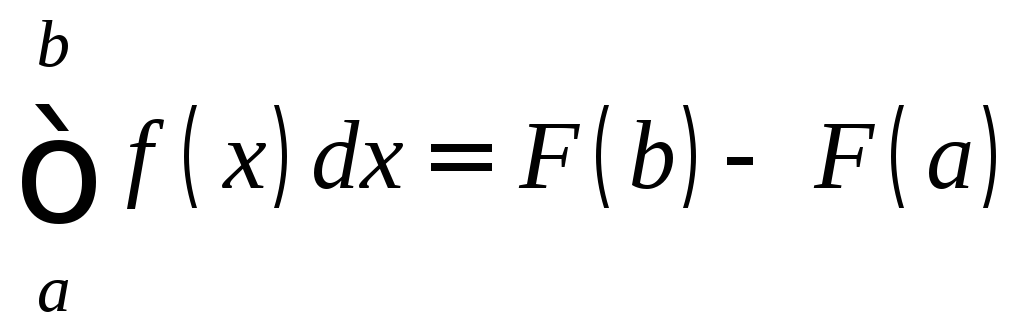. (4)
Формула (4) называется формулой Ньютона-Лейбница.
Доказательство.
Т.к. f(x)С[a;b],
то она на [a;b]
имеет первообразную. Пусть F
- произвольная первообразная для f(x)
на [a;b],
и пусть
.
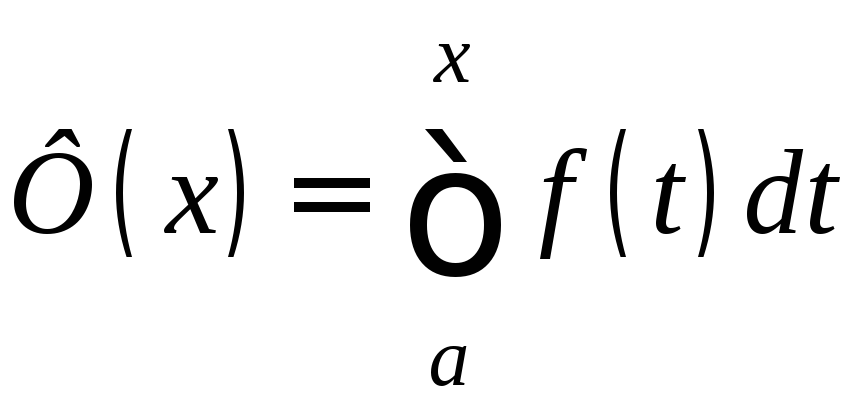По теореме 1 функцияФ(x)
также является первообразной для f
на [a;b].
Итак, функции F(x)
и Ф(х)
являются первообразными для одной и
той же функции, значит, они отличаются
на постоянную, т.е. Ф(x)=F(x)+C0,
x
[a;b].
Следовательно,
.
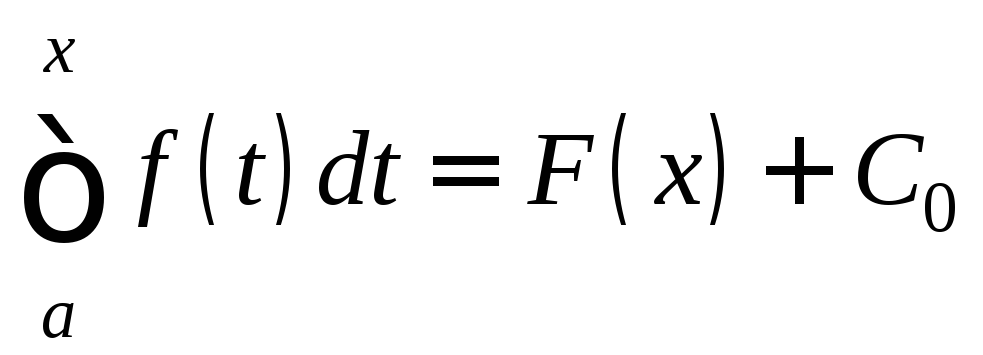Положим здесь
x=a,
получим, С0=-F(a).
Отсюда,
.
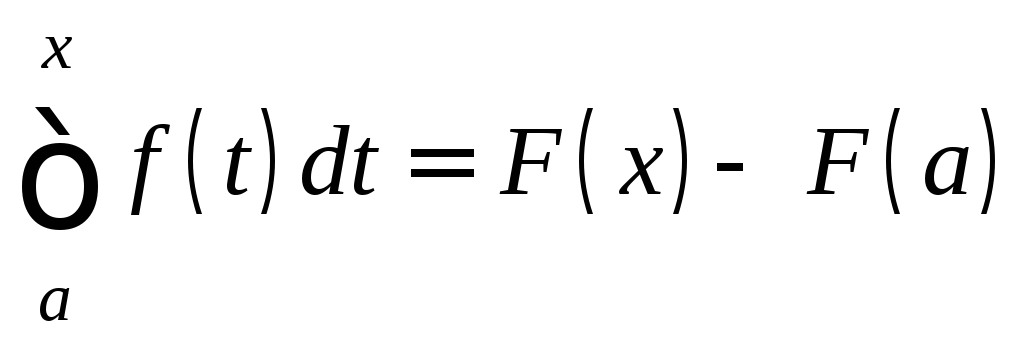Положим здесь
x=b,
получим
.
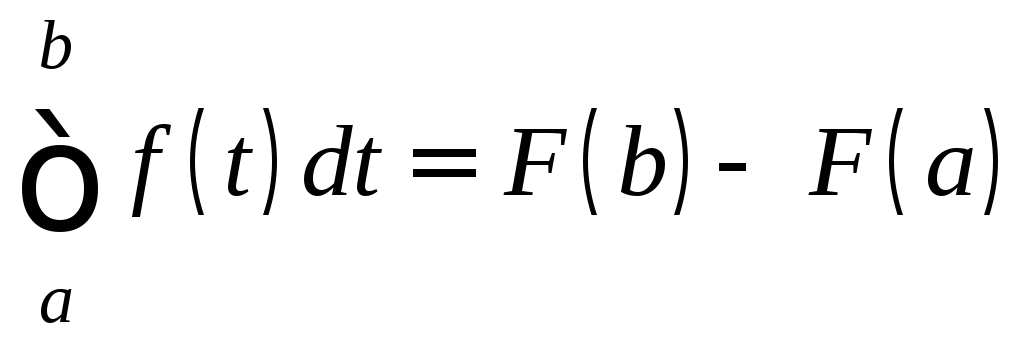Обозначим
.
Тогда формула Ньютона-Лейбница примет
вид
.
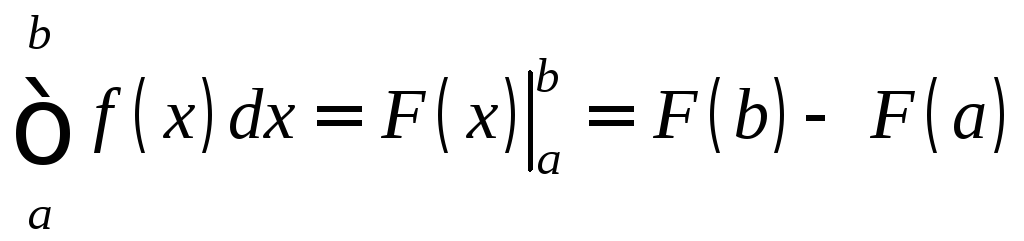§6. Интегрирование по частям и замена переменной в определённом интеграле. Интегрирование чётных и нечётных функций.
Определение. Функция f(x) называется непрерывно дифференцируемой на [a;b], если она непрерывна на [a;b] и её производная f тоже непрерывна на [a;b].
Множество всех функций, определённых и непрерывно дифференцируемых на [a;b] обозначают C1[a;b].
Теорема 1. Если
u=u(x)
и v=v(x)
непрерывно дифференцируемы на [a;b],
то
. (1)
Доказательство.
По условию u
и v
имеют непрерывные производные на [a;b].
Следовательно, функция uv
имеет непрерывную производную на [a;b].
(u(x)v(x))=u
(x)v(x)+u(x)v
(x).
Отсюда
следует, что функция uv
является первообразной для (u
v+uv
), непрерывной
на [a;b].
Тогда по формуле Ньютона-Лейбница
.
По свойству интеграла
.
Отсюда получаем (1).
Замечание. u
(x)dx=du,
v
(x)dx=dv,
следовательно, формула (1) может быть
записана в виде
.
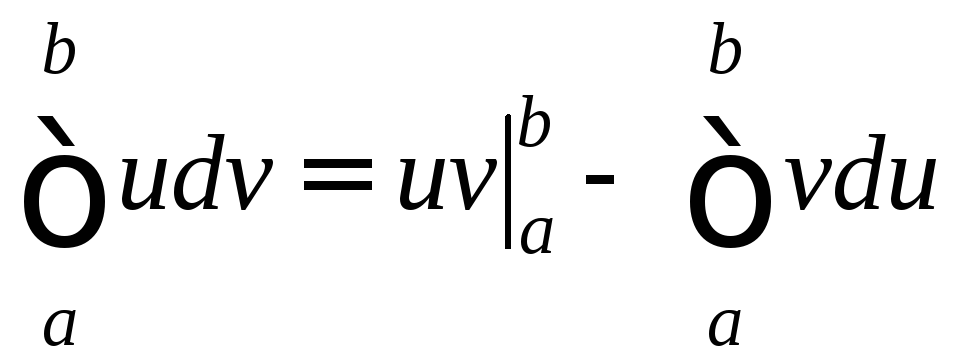Теорема 2. Пусть
1) f
C[a;b],
2) x=φ(t)
C1[α;β]
–однозначная функция и t
[α;β]
x=φ(t)
[a;b]
(т.е. φ[α;β][a;b]),
3) φ(α)=a, φ(β)=b.
Тогда справедлива
формула
.
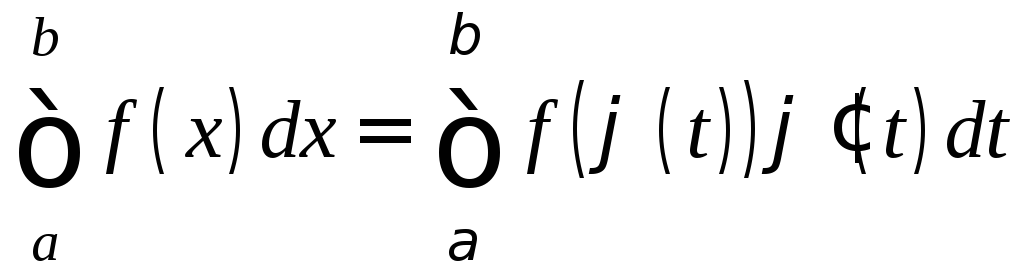(2)
Доказательство.
Т.к. f
C[a;b],
то она имеет первообразную. По формуле
Ньютона-Лейбница
. (3)
Рассмотрим функцию F(φ(t)).
(F(φ(t))=Fx(φ(t))φt(t)=f(φ(t))φ (t), т.к. F (x)=f(x). Отсюда следует, что функция F(φ(t)) является первообразной для f(φ(t))φ (t) на [α;β]. Поэтому, применяя формулу Ньютона-Лейбница, получим
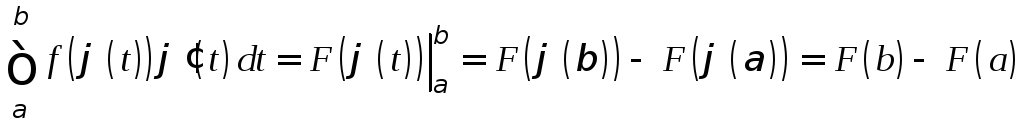. (4)
Из равенств (3) и
(4) следует равенство (2)
Пример.
.
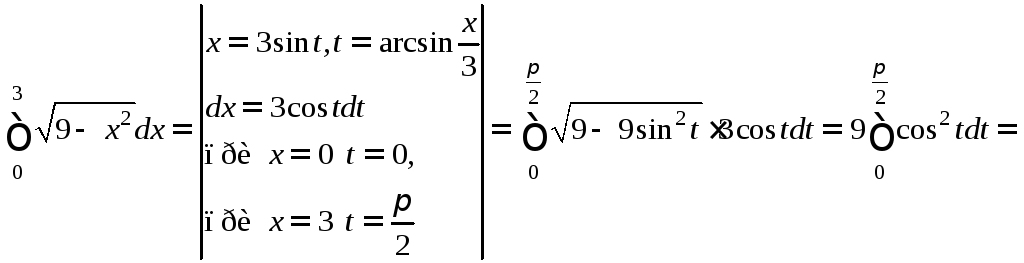
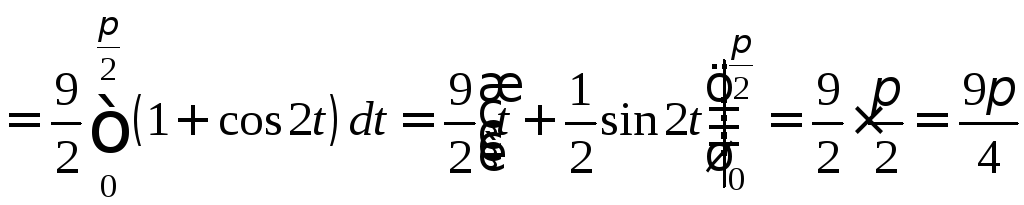Теорема 3. Пусть
f
R[-a;a],
тогда
если f
- чётная на [-a;a],
то
;
если f
- нечётная
на [-a;a],
то
.
Доказательство.
;
.
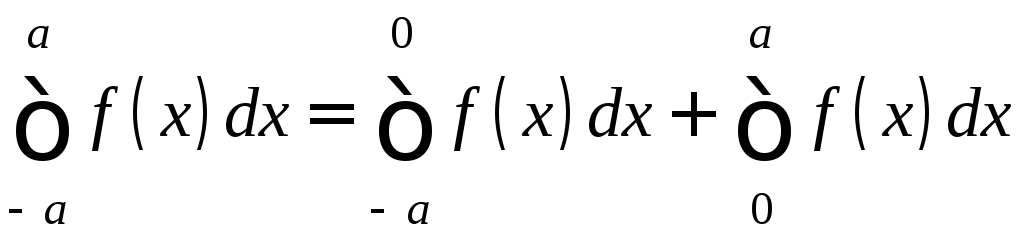Следовательно,
.
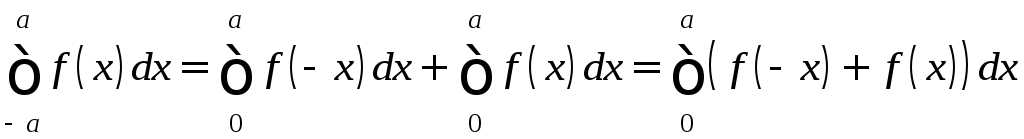Если f
– чётная, то f(x)+f(-x)=2f(x).
Следовательно,
.
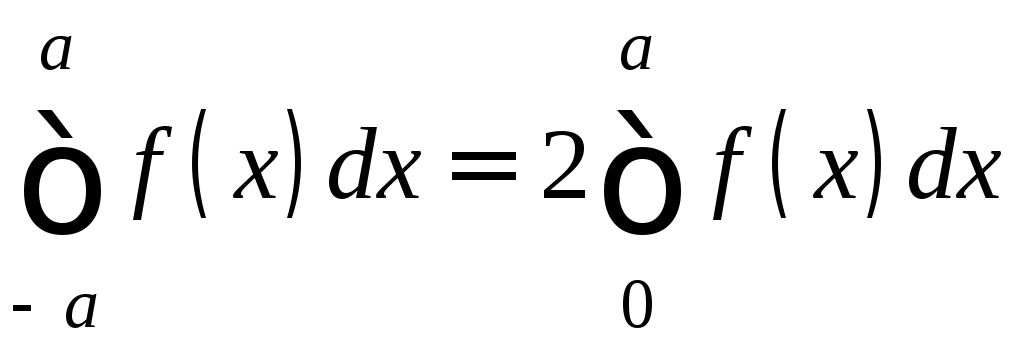Если f
– нечётная, то f(x)+f(-x)=0.
Следовательно,
.
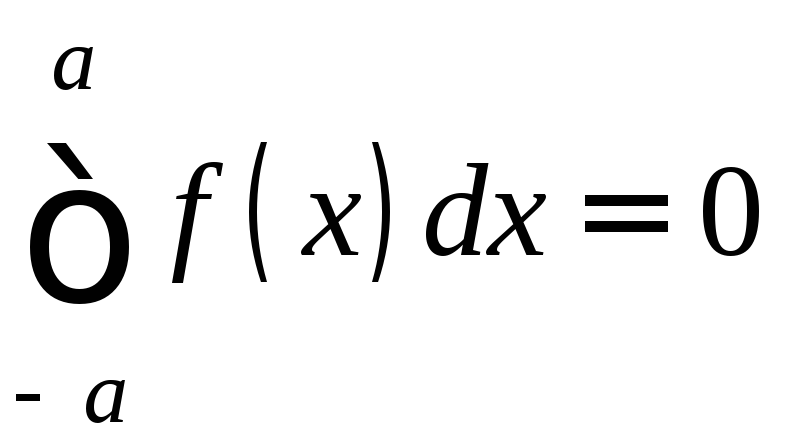