§2. Свойства неопределённого интеграла

1. ,

Доказательство.

.

2.

Доказательство.

dF(x)=F'(x)dx=f(x)dx  .

3. Если f(x) имеет первообразную на <a;b> и к≠0, то функция кf(x) тоже имеет первообразную на <a;b>, причём

. (1)

Доказательство.

(kF(x))'=kF'(x)=кf(x)  функция kF является первообразной для kf на <a;b> =>

Далее . Итак, левая часть равенства (1) представляет собой совокупность функцийkF(x)+C₁, а правая состоит из функций вида kF(x)+kC. В силу произвольности С₁ и С оба множества совпадают.

4. Если функции f и g имеют первообразные на <a;b>, то и функция f±g имеет на <a;b> первообразную, причём

. (2)

Доказательство.

Пусть =F(x)+C₁, =G(x)+C₂.

Рассмотрим функцию Ф(x)=F(x)±G(x),

Ф'(x)=F'(x)±G'(x)=f(x)±g(x)  . Следовательно, левая часть равенства (2) состоит из функций F(x)±G(x)+C, а правая из функций (F(x)+C₁)±(G(x)+C₂)= F(x)±G(x)+C₁±C₂. Ввиду произвольности С₁, С₂, С эти множества совпадают.

Свойства 3 и 4- линейные свойства интеграла.

Следствие. Пусть f и g имеют первообразные на <a;b> и хотя бы одно из чисел α, β отлично от 0, тогда функция αf(x)+βg(x) имеет первообразную на <a;b>, причём

.

§3. Основная таблица интегралов

Из таблицы производных основных элементарных функций получаем основную таблицу интегралов.

1.

2.

3.

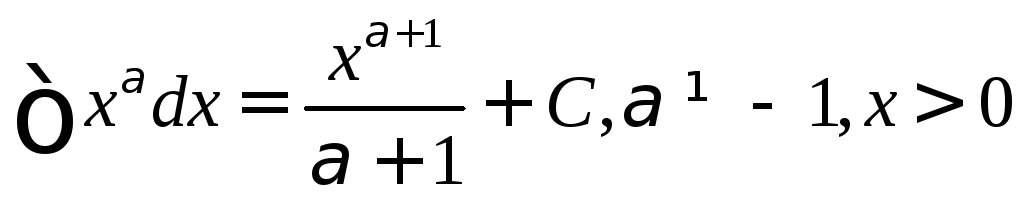
4.

5.

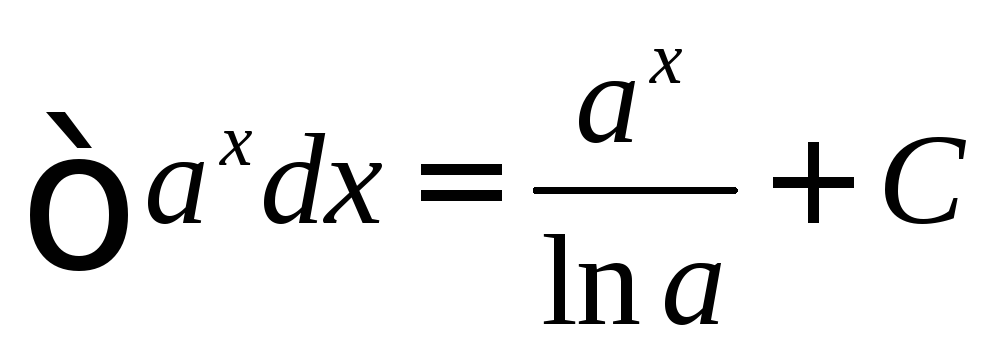
6.

7.

8.

9.

10.

11.

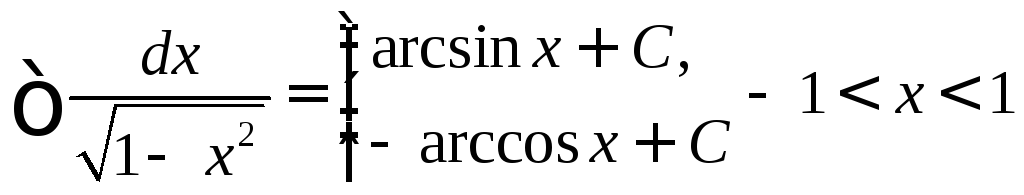
12.

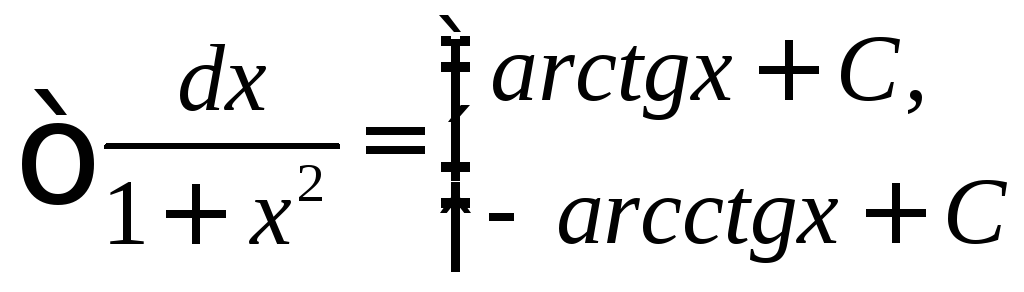
13.

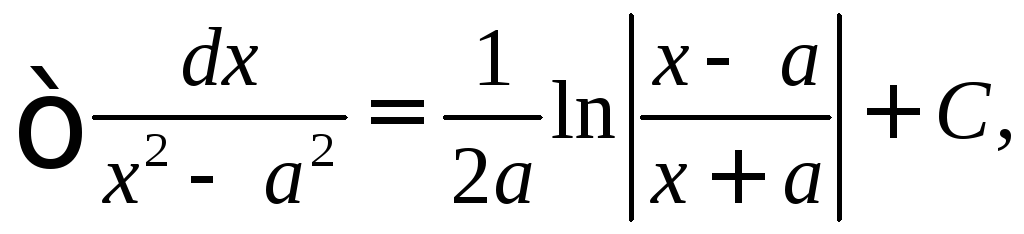
14.

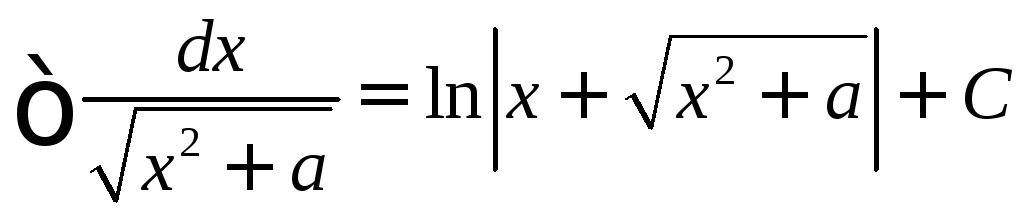
15.

16.

17.

18.

Как известно, производная от элементарной функции является элементарной функцией. Т. е. операция дифференцирования не выводит нас из класса элементарных функций. При интегрировании интегралы от некоторых элементарных функций не являются элементарными функциями.

Примеры.

1. –интеграл Пуассона

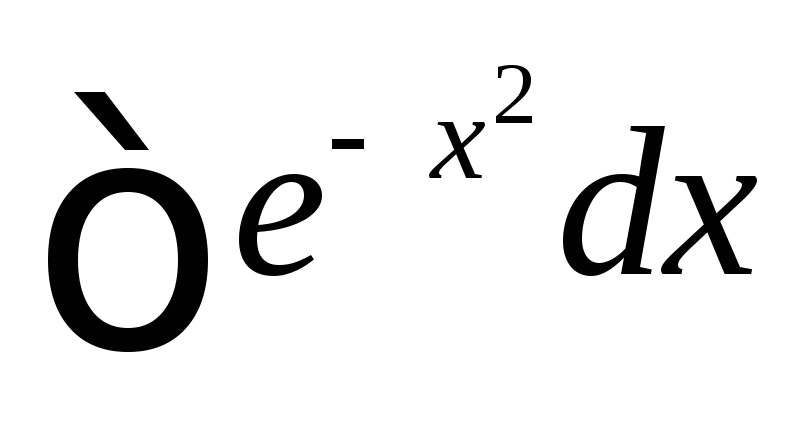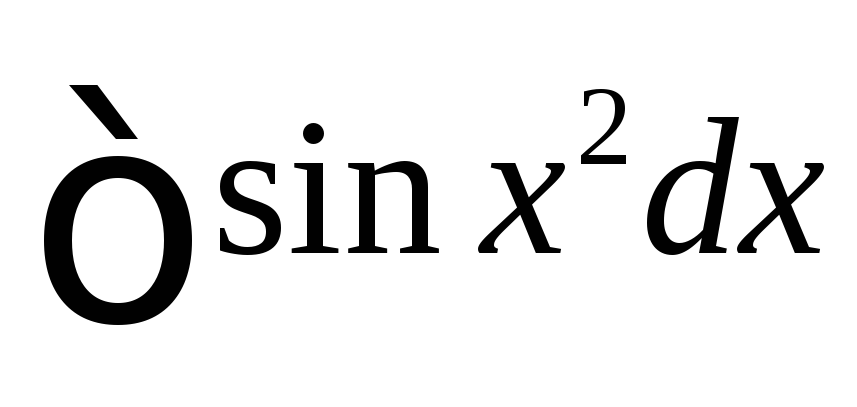
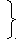2. интегралы

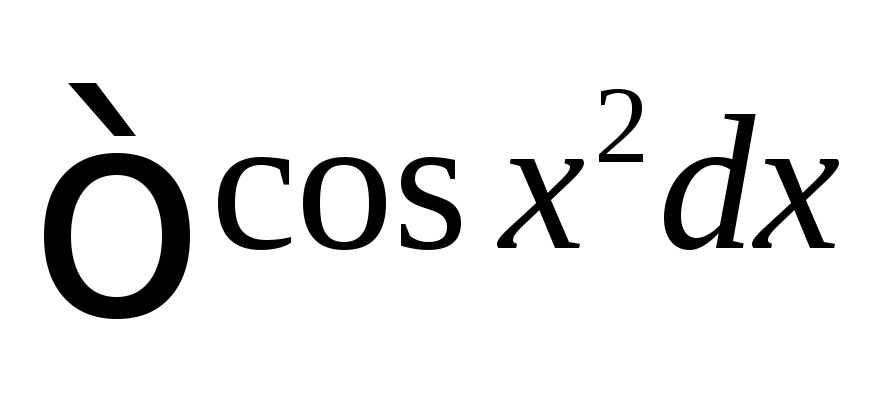3. Френеля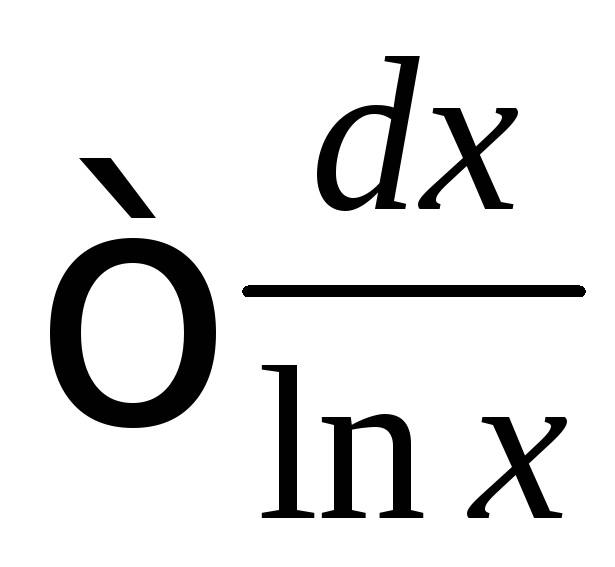

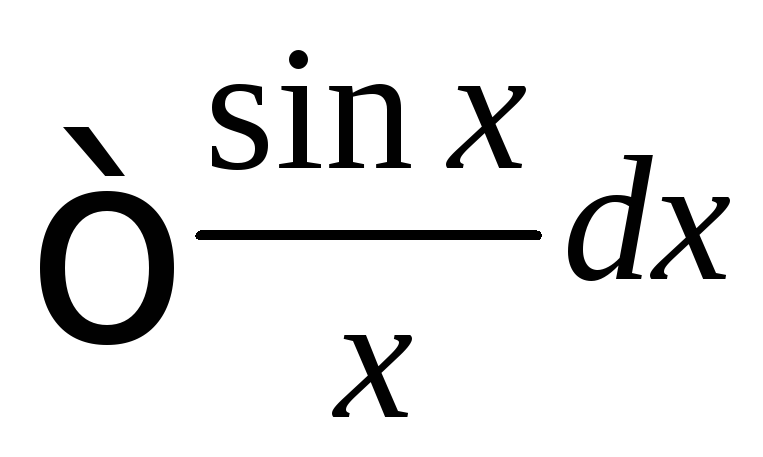
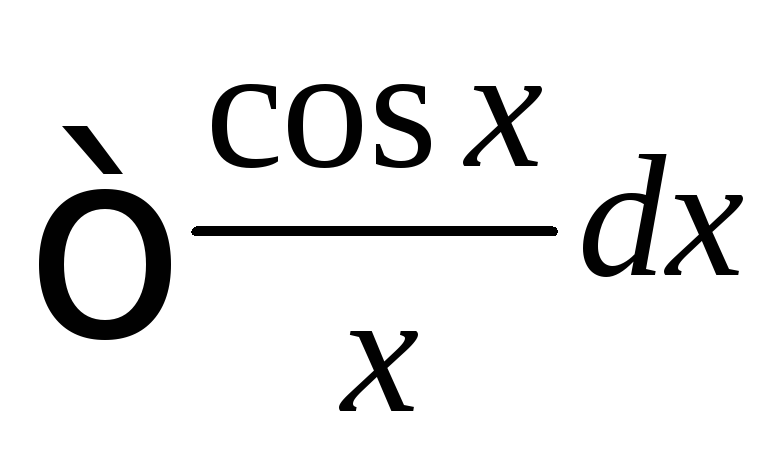
4. 

5. 

6. 

Если для функции f первообразная является элементарной функцией, то говорят, что выражается через элементарные функции или, что этот интеграл вычисляется. Далее выделим те элементарные функции, интегралы от которых вычисляются.

§4. Основные методы интегрирования

I. Метод введения нового аргумента

По определению неопределённого интеграла ,x<a;b> - независимая переменная. Эта формула инвариантна относительно х, т.е. в формуле х может быть как независимой переменной, так и непрерывно дифференцируемой функцией.

Теорема1. Если , тогдеu=φ(x) – непрерывно дифференцируемая функция.

Доказательство.

Имеем

, (1)

где х – независимая переменная. С другой стороны, дан , гдеu=φ(x)– непрерывно дифференцируемая функция, значит, du=φ'(x)dx. Тогда

f(u)du=f(φ(x))φ'(x)dx. (2)

Рассмотрим сложную функцию F(u)=F(φ(x)).

[F(φ(x))]'=F'(u)φ'(x)=f(u)φ'(x)=f(φ(x))φ'(x), т.е. функция F(φ(x)) является первообразной для f(φ(x))φ'(x). Следовательно, , или по (2).

Примеры.

1. - непрерывно дифференцируемая функция на

2. .

3. Обобщим формулы (11) и (12) таблицы интегралов

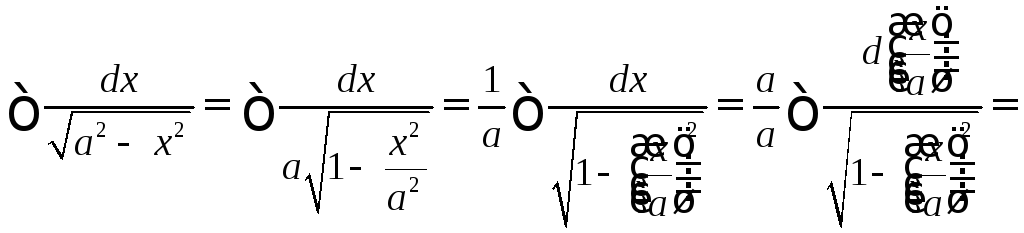
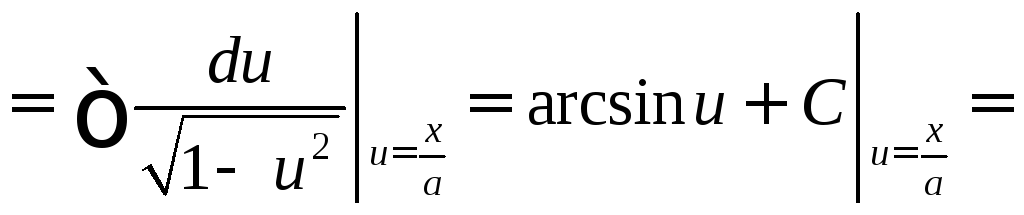
Итак, .

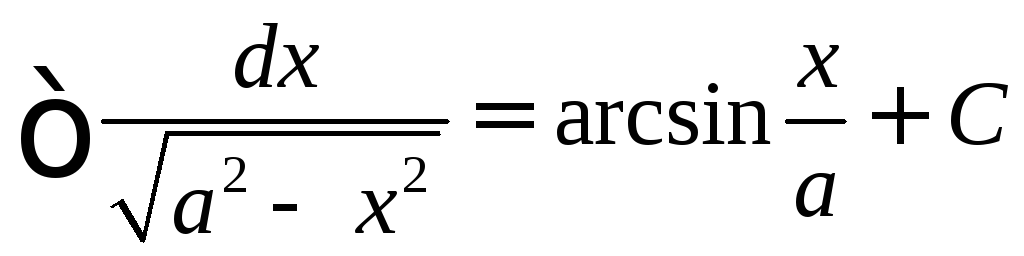(аналогично)

4.

, .

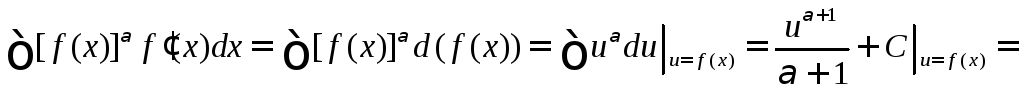
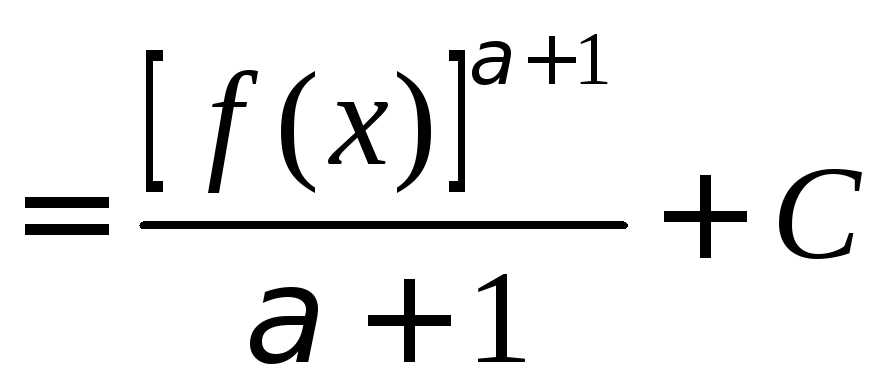Если α=-1, то

.

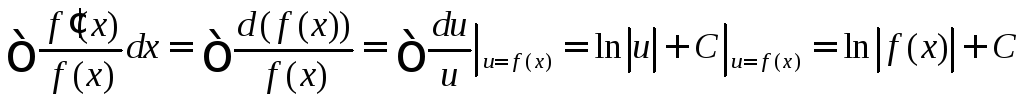5. .

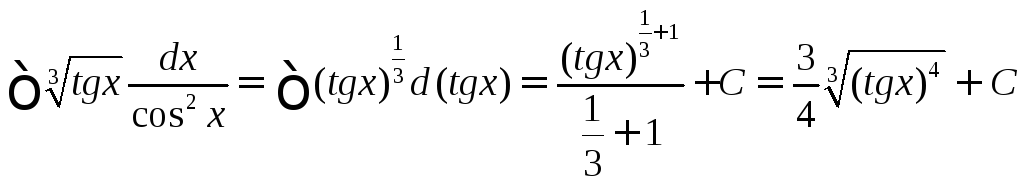II. Метод подстановки

Теорема 2. Пусть y=f(x) непрерывна на ∆_x, x=φ(t) – монотонная, непрерывно дифференцируемая на ∆_t. Пусть определена сложная функция f(φ(t)) на ∆_t (множеством значений функции φ(t) является промежуток ∆_x). Тогда

. (3)

Доказательство.

Продифференцируем обе части равенства (3):

.

Значит, обе части формулы (3) имеют один и тот же дифференциал и, следовательно, выражают собой одно и то же семейство первообразных для функции f(x).

Итак, для вычисления интеграла с помощью подстановкиx=φ(t) надо выразить х через t, dx – через t и dt, т.е. dx=φ'(t)dt. Чтобы после вычисления интеграла вернуться к переменной х, надо в полученной функции заменить t значением, которое находится из соотношения t=φ^-1(x) (существование обратной функции следует из монотонности φ(t)).

Линейная подстановка

.

Докажем двумя способами (с помощью I и II)

1 способ.

.

2 способ.

.

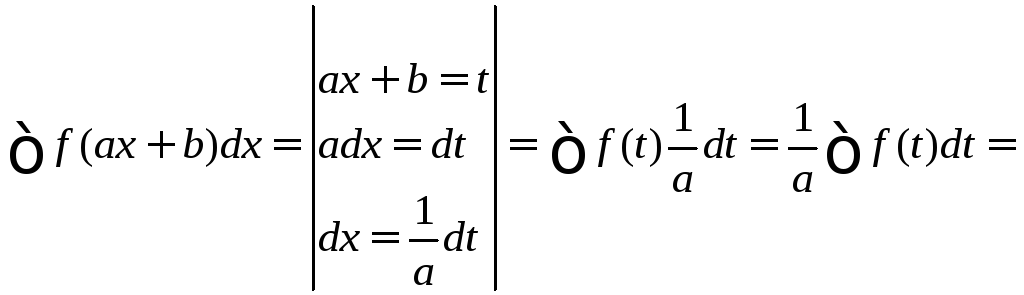
Пример.

.
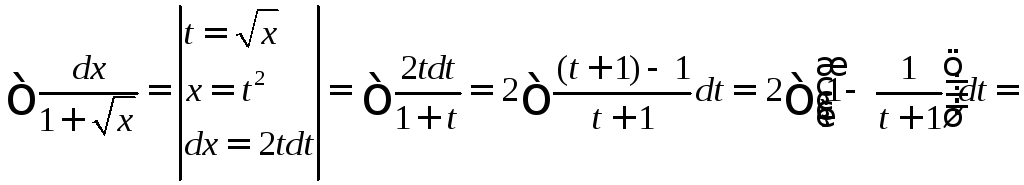
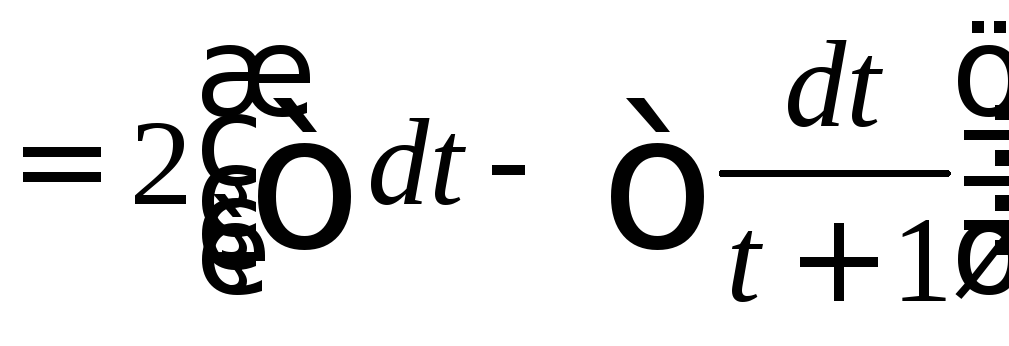
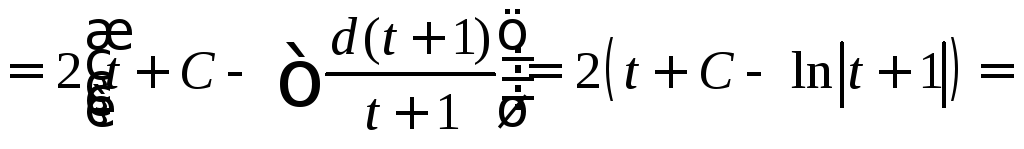