III. Интегрирование по частям

Теорема 3. Пусть функции u=u(x) и v=v(x) дифференцируемы на промежутке ∆. Пусть на ∆ функция имеет первообразную. Тогда функцияна ∆ имеет первообразную и справедлива формула

. (4)

Доказательство.

По правилу дифференцирования произведения имеем:

.

Следовательно, . (5)

По условию существует интеграл . По свойству интеграла . Поэтому существует интеграл правой части (5), следовательно, существует интеграл и левой части:

.

Относя в последнем равенстве С ко второму интегралу получим (4).

Замечание. Т.к. v'(x)dx=dv, u'(x)dx=du, то (4) можно записать в виде

. (6)

Формула (6) сводит вычисление к вычислению, что иногда бывает легче сделать. Для применения (6) надо подынтегральное выражение разбить на 2 сомножителя u и dv (в dv входит dx).

Выделим основные типы интегралов, вычисляемые методом интегрирования по частям.

I. Подынтегральная функция имеет вид P(x)e^ax, P(x)cosax, P(x)sinax, где P(x) – многочлен, a. В таких интегралах заu(x) надо принять многочлен P(x) и формулу интегрирования по частям применять столько раз, какова степень многочлена.

Пример.

.

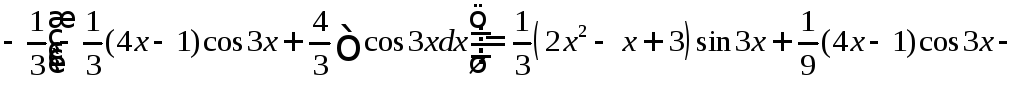
II. Подынтегральная функция содержит в качестве множителя одну из функций lnx, arcsinx, arccosx, arctgx, arcctgx.

В этом случае за u(x) надо взять эту функцию.

Пример.

.

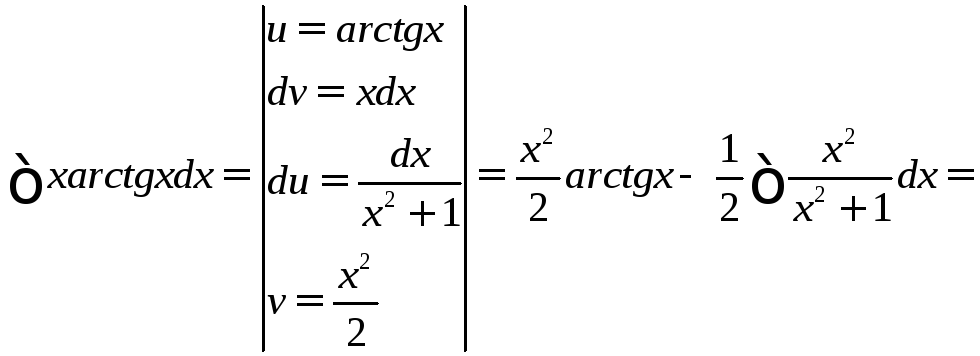
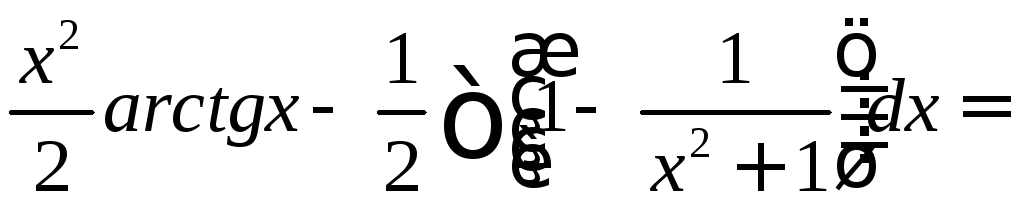
III. Подынтегральная функция имеет вид: e^axsinbx, e^axcosbx, cos(lnx), sin(lnx).

Формула интегрирования по частям применяется последовательно 2 раза, причём оба раза за u(x) выбирается одна и та же функция (либо показательная, либо тригонометрическая). После этого получается линейное уравнение относительно исходного интеграла.

Пример.

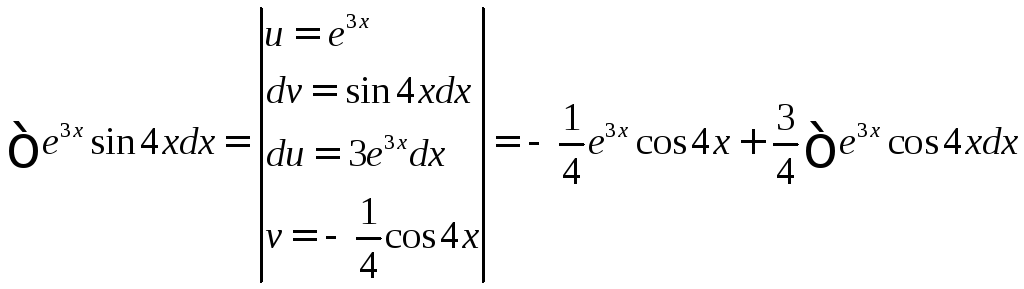
Пусть . Получим уравнение:



.

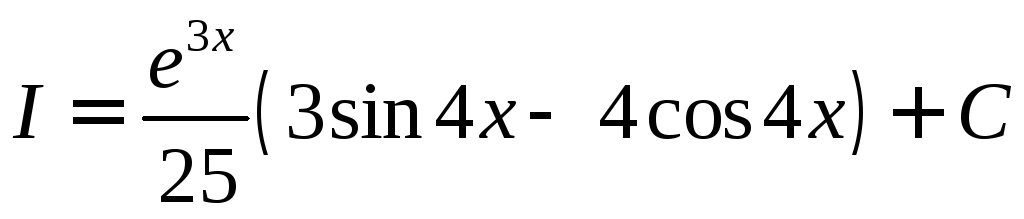IV. С помощью метода интегрирования по частям можно вывести так называемые рекуррентные формулы, дающие возможность свести некоторые интегралы к интегралам того же типа, но более простым по своей структуре.

§5. Интегрирование рациональных выражений

1. Основные понятия

Определение. Рациональной функцией (или рациональной дробью) называется функция вида =, гдеP_n, Q_m – многочлены степеней n и m соответственно. Если n<m, то рациональная дробь называется правильной, в противном случае (n≥m) – неправильной.

Если рациональная дробь неправильная, то её с помощью деления можно представить в виде суммы многочлена (целая часть) и правильной рациональной дроби, т.е. 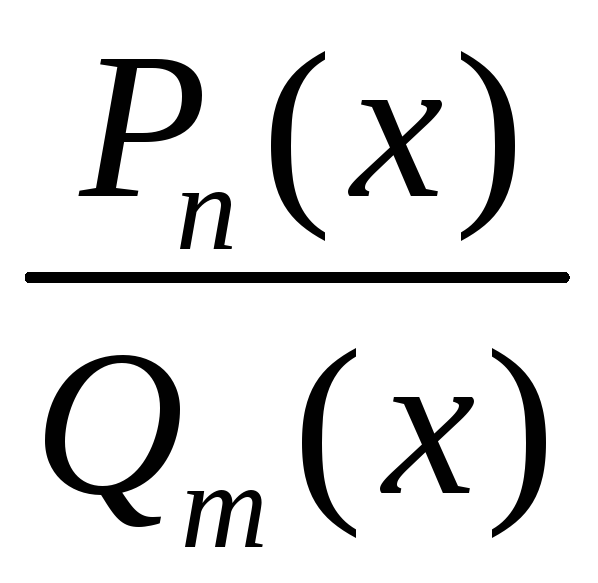=+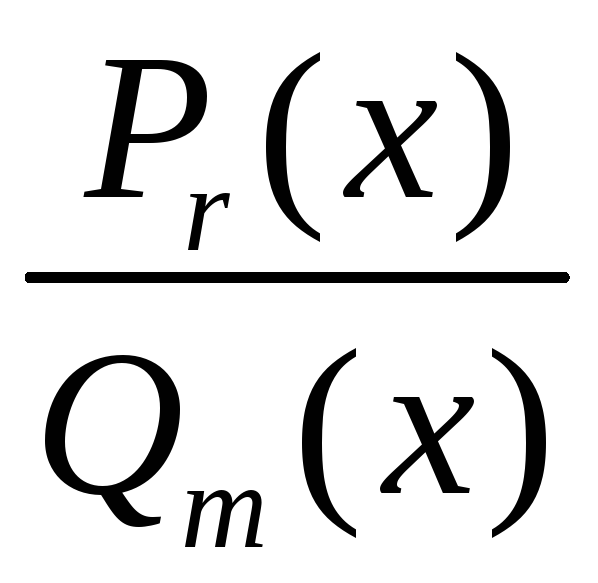, гдеP_n-m(x) – многочлен степени n – m, r <m .

Примеры.

1) Метод деления

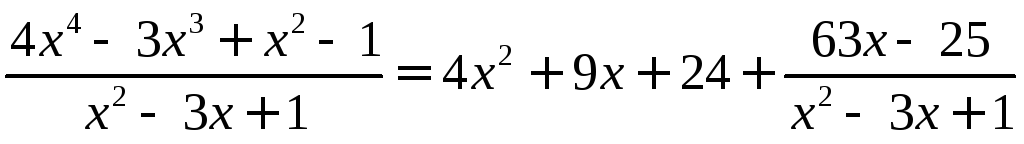
4x⁴– 3x³+ x² – 1 x² - 3x+ 1

4x⁴–12x³+4x² 4x² +9x+24

9x³ – 3x² - 1

9x³–27x² + 9x

24x² – 9x – 1

24x²–72x + 24

63x – 25

2) Метод преобразований

.

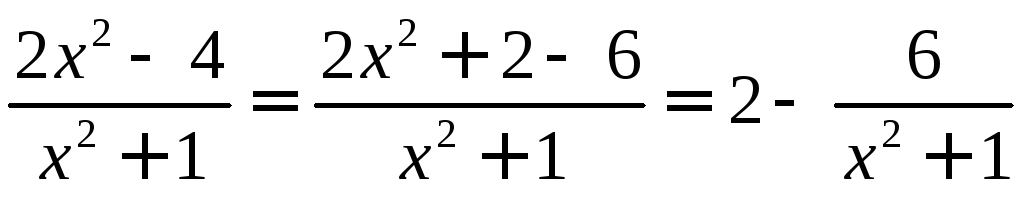2. Интегрирование простейших дробей.

Определение. Простейшими дробями называются дроби следующих четырёх типов:

1) ; 2); 3); 4) ,

где A, M, N, a, p, q , трехчлен не имеет действительных корней (т. е. D=p²–4q<0).

1);

2);

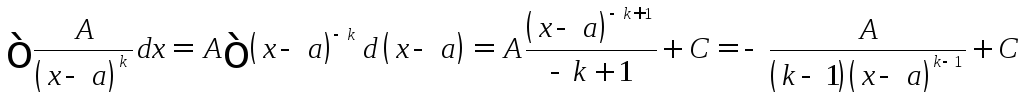3).

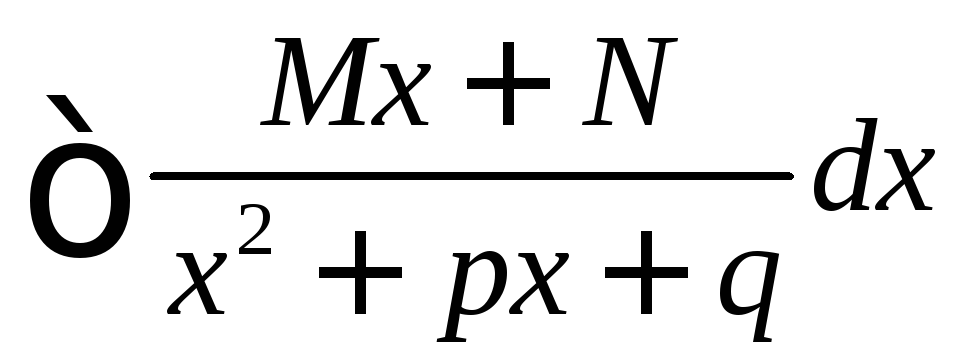В числителе выделяется выражение равное производной знаменателя. Разделив затем почленно, получим табличный интеграл и интеграл вида

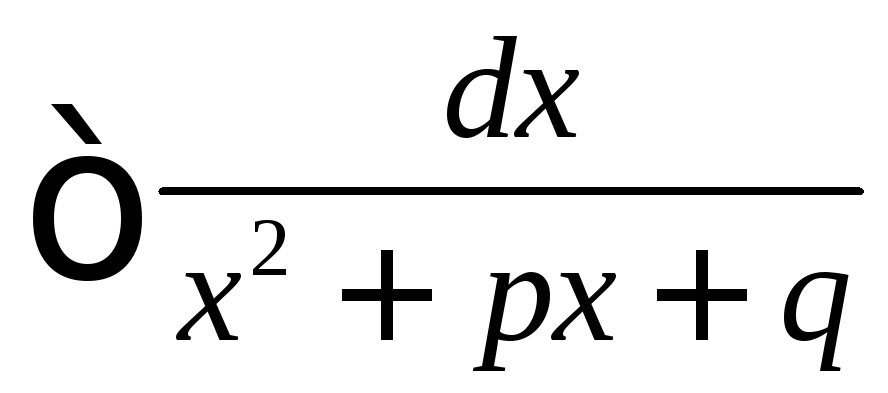, который вычисляется путём выделения полного квадрата в знаменателе.

Пример.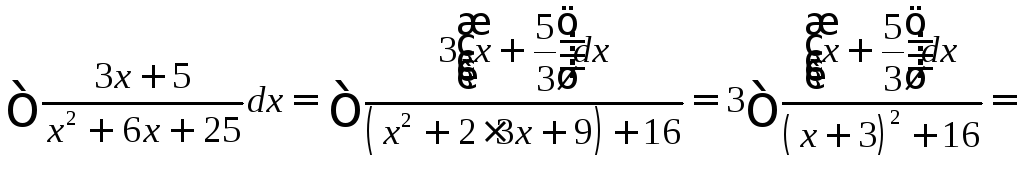

.

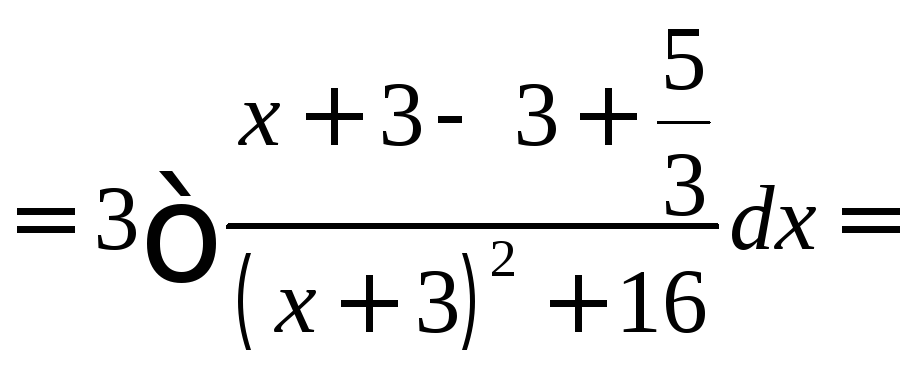
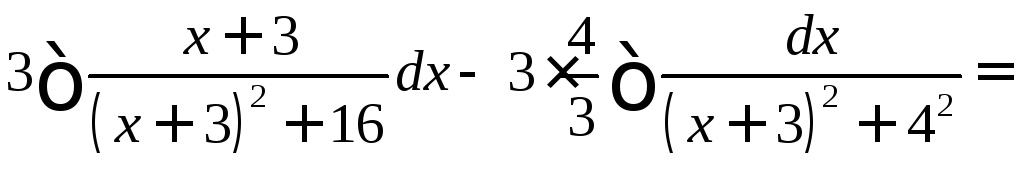
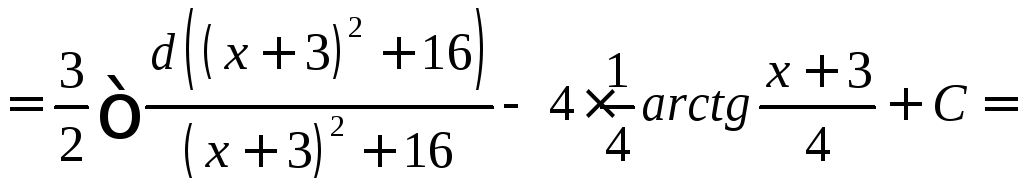
4) 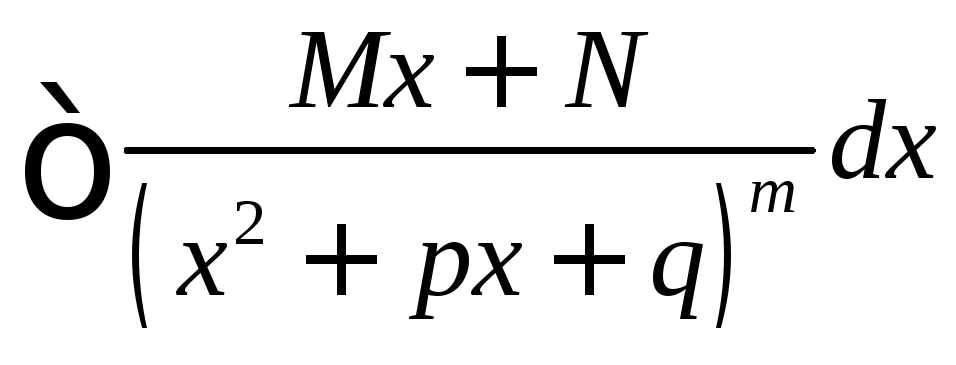вычисляется аналогично интегралу вида 3) с применением рекуррентной формулы (7).