
- •Интегральное исчисление функций одной переменной
- •I. Неопределенный интеграл
- •§1. Первообразная
- •§2. Свойства неопределённого интеграла
- •§3. Основная таблица интегралов
- •§4. Основные методы интегрирования
- •I. Метод введения нового аргумента
- •II. Метод подстановки
- •III. Интегрирование по частям
- •§5. Интегрирование рациональных выражений
- •1. Основные понятия
- •2. Интегрирование простейших дробей.
- •1) ; 2); 3); 4) ,
- •3. Разложение правильной рациональной дроби на сумму простейших
- •4. Интегрирование рациональной функции
- •§6. Интегрирование иррациональных функций
- •§7. Интегрирование выражений, содержащих тригонометрические
- •II. Определенный интеграл
- •§1. Понятие определённого интеграла
- •§2. Нижние и верхние интегральные суммы
- •§3. Некоторые классы интегрируемых функций
- •1. Интегрируемость непрерывных функций.
- •2. Интегрируемость монотонной функции.
- •3. Интегрируемость функций, имеющих конечное число точек разрыва.
- •§4. Основные свойства определённого интеграла.
- •§5. Определённый интеграл с переменным верхним пределом. Существование первообразной функции. Формула Ньютона-Лейбница.
- •§6. Интегрирование по частям и замена переменной в определённом интеграле. Интегрирование чётных и нечётных функций.
§3. Некоторые классы интегрируемых функций
1. Интегрируемость непрерывных функций.
Теорема 1. Если функция f(x) определена и непрерывна на [a;b] (a<b), то f интегрируема на [a;b].
Доказательство.
![]() Т.к. f
непрерывна на [a;b],
то она ограничена на нём и равномерно
непрерывна на нём (теорема Кантора).
Возьмём произвольное разбиение
Т.к. f
непрерывна на [a;b],
то она ограничена на нём и равномерно
непрерывна на нём (теорема Кантора).
Возьмём произвольное разбиение
![]() отрезка [a;b]
и составим разность
отрезка [a;b]
и составим разность
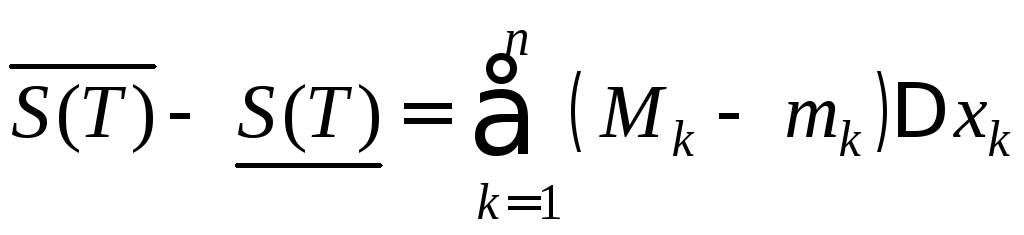 ,
где
,
где![]() .
Т.к.f
непрерывна на [xk-1;xk],
то mk
является наименьшим, а Mk-наибольшим
значением f
на [xk-1;xk],
т.е. существуют xk′
и xk″,
такие, что f(xk′)=mk,
f(xk″)=Mk.
Следовательно,
.
Т.к.f
непрерывна на [xk-1;xk],
то mk
является наименьшим, а Mk-наибольшим
значением f
на [xk-1;xk],
т.е. существуют xk′
и xk″,
такие, что f(xk′)=mk,
f(xk″)=Mk.
Следовательно,
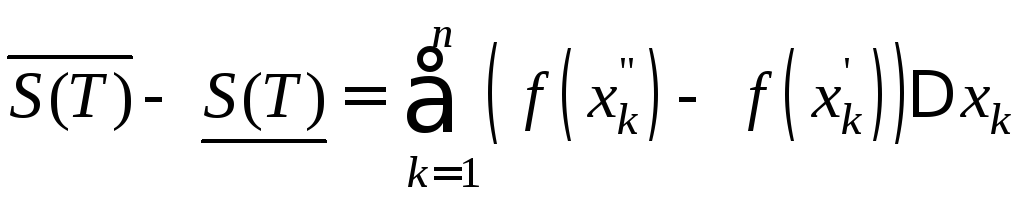 . (1)
. (1)
Выберем произвольное
ε>0.
Т.к. f
равномерно непрерывна на [a;b],
то для выбранного ε>0
существует δ>0,
такое, что x′,
x″![]() [a;b],
удовлетворяющих условию |x′-x″|<δ,
выполнено, |f(x″)-f(x′)|<
[a;b],
удовлетворяющих условию |x′-x″|<δ,
выполнено, |f(x″)-f(x′)|<![]() .
.
Пусть Т-
такое, что λ<δ.
Тогда |xk″-xk′|≤|xk-1;xk|<∆xk=λ<δ
и, следовательно, выполняется неравенство
|f(xk″)-f(xk′)|<![]() .
Тогда из (1) следует, что
.
Тогда из (1) следует, что

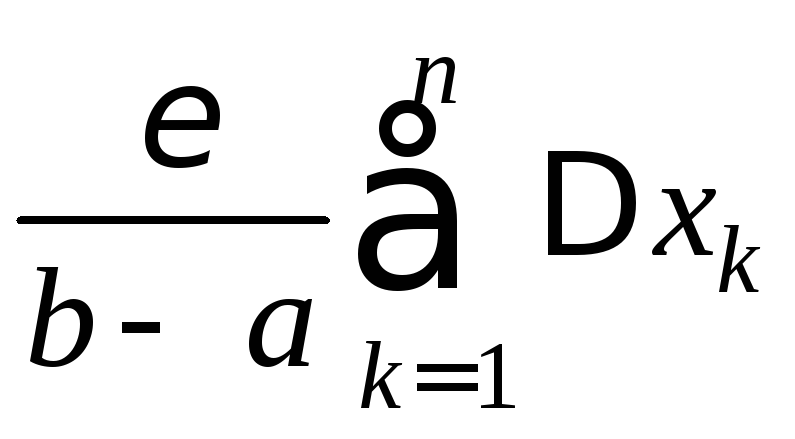 =
=![]() .
.
Получили, что для
любого разбиения Т,
такого, что λ<δ
выполнено
![]() .
Следовательно,
.
Следовательно,![]() .
Значит, согласно критерию интегрируемости,
функцияf
интегрируема на [a;b]
.
Значит, согласно критерию интегрируемости,
функцияf
интегрируема на [a;b]
![]()
2. Интегрируемость монотонной функции.
Теорема 2. Если функция f(x) определена и монотонна на [a;b], то она интегрируема на [a;b].
Доказательство.
![]() Пусть f(x)-монотонно
возрастает на [a;b].
Выберем произвольное разбиение
Пусть f(x)-монотонно
возрастает на [a;b].
Выберем произвольное разбиение
![]() отрезка [a;b].
Т.к. f
возрастает, то mk=f(xk-1),
Mk=f(xk);
Mk>mk
для любого
отрезка [a;b].
Т.к. f
возрастает, то mk=f(xk-1),
Mk=f(xk);
Mk>mk
для любого
![]() ,f(xk)>f(xk-1).
Пусть ε-произвольное
положительное число. Выберем
,f(xk)>f(xk-1).
Пусть ε-произвольное
положительное число. Выберем
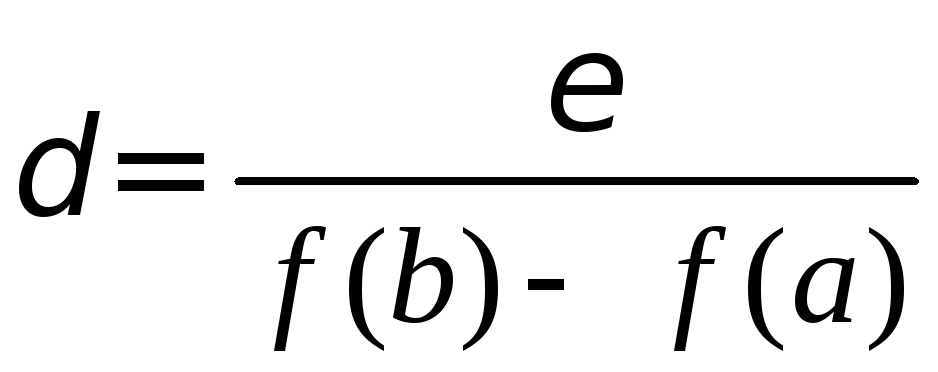 .
ПустьТ-
такое, что λ<δ,
тогда
.
ПустьТ-
такое, что λ<δ,
тогда
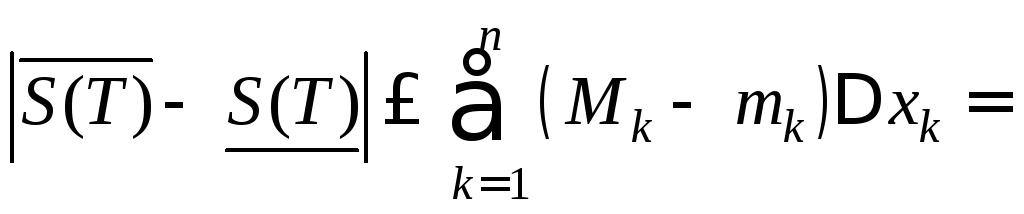

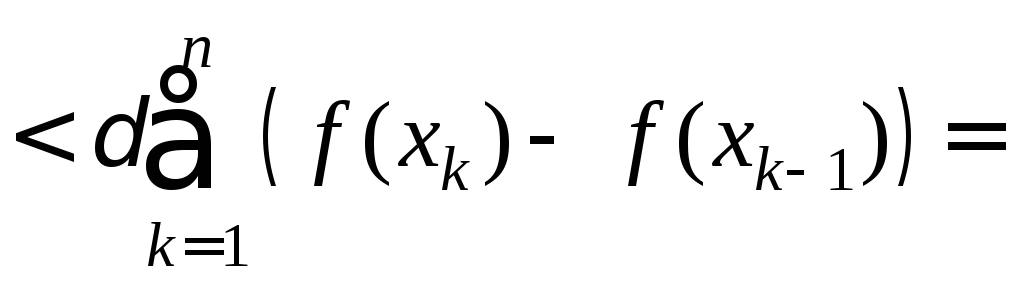
 .
.
Получили, что ε>0
δ>0,
такое, что для любого разбиения Т:
λ<δ
выполнено
![]() .
Это значит, что
.
Это значит, что![]() .
Следовательно,f
интегрируема на [a;b]
.
Следовательно,f
интегрируема на [a;b]
![]()
3. Интегрируемость функций, имеющих конечное число точек разрыва.
Теорема 3. Если функция f(x) определена, ограничена на [a;b] и имеет конечное число точек разрыва, то она интегрируема на [a;b].
Определение. Функция f называется кусочно непрерывной на [a;b], если она непрерывна на [a;b], кроме конечного числа точек разрыва, и притом только первого рода.
Следствие. Если функция f кусочно непрерывна на [a;b], то она интегрируема на [a;b].
Лемма. Пусть
f
и g
определены на [a;b]
и f(x)=g(x)
x![]() (a;b).
Тогда, если f
интегрируема на [a;b],
то и g
интегрируема на [a;b]
и
(a;b).
Тогда, если f
интегрируема на [a;b],
то и g
интегрируема на [a;b]
и
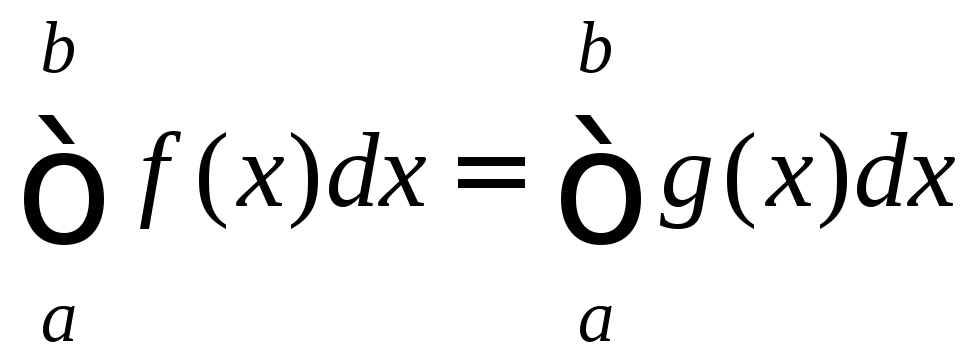 .
.
Лемма утверждает, что если f интегрируема на [a;b], то её интегрируемость и величина определённого интеграла не изменится, если изменить значения функции f на концах отрезка и также в любом конечном числе точек отрезка.
Множество всех
функций, интегрируемых по Риману на
[a;b]
обозначают R[a;b].
Т. о., f![]() R[a;b]
тогда и только тогда, когда f
R[a;b]
тогда и только тогда, когда f![]() R(a;b).
R(a;b).
Расширим понятие
определённого интеграла. Будем считать
по определению, что
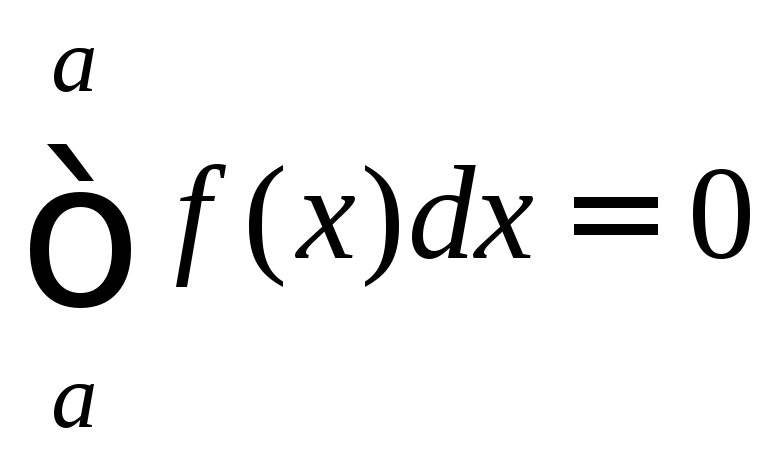 .
.
§4. Основные свойства определённого интеграла.
1.
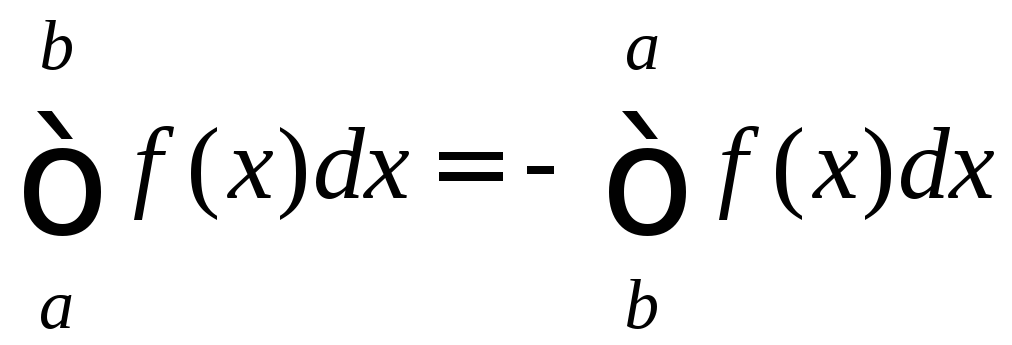 . (1)
. (1)
Доказательство.
![]()
 Пусть a<b.
Выберем произвольное разбиение
Пусть a<b.
Выберем произвольное разбиение
![]() отрезка [a;b]
и произвольно выберем точки ξk
отрезка [a;b]
и произвольно выберем точки ξk![]() [xk-1;xk].
Составим
[xk-1;xk].
Составим
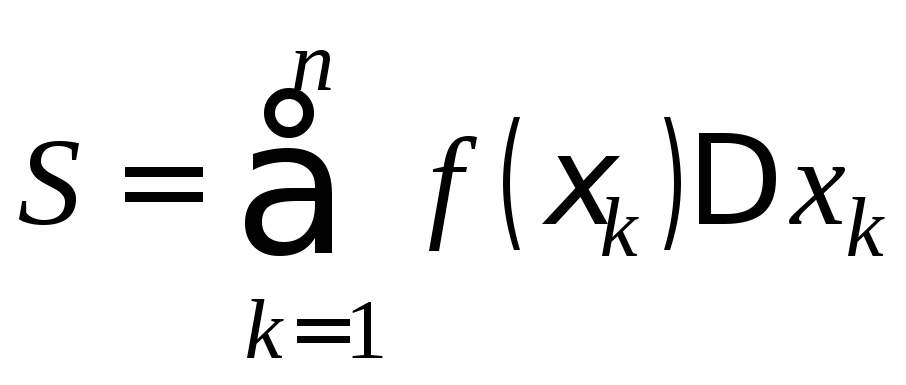 .
.
Будем считать
а-верхним пределом, b-нижним пределами интегрирования (для выбранных Т и ξk):
b=x0′>x1′>x2′>…>x′n-1>x′n=a, ∆x′k=x′k-x′k-1<0,
![]() .
.
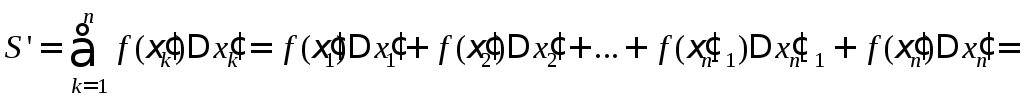
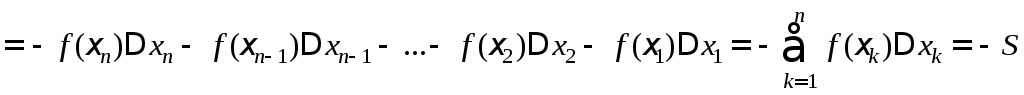 .
Следовательно, S′=-S. (2)
.
Следовательно, S′=-S. (2)
По условию
существует
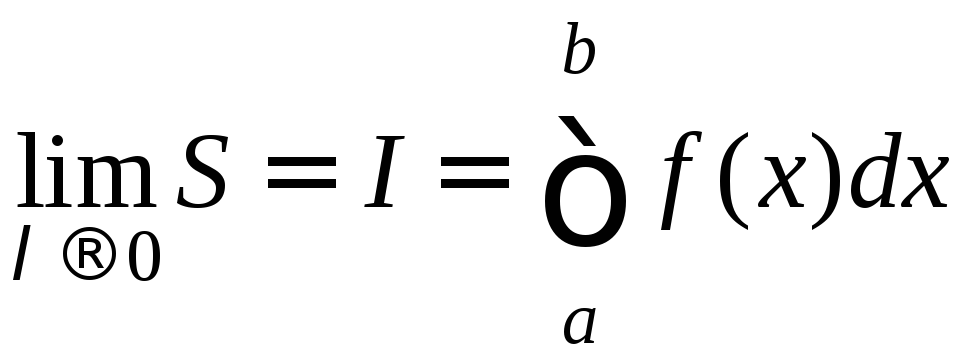 .
Следовательно, существует
.
Следовательно, существует
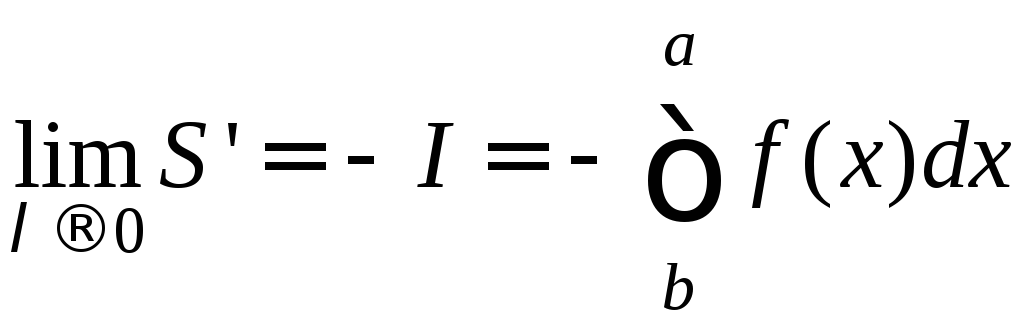 .
Переходя в равенстве (2) к пределу при
0,
получим равенство (1).
.
Переходя в равенстве (2) к пределу при
0,
получим равенство (1).
![]()
2. Если
f
и g
интегрируемы на [a;b],
то и функция f+g
также интегрируема на [a;b],
причём
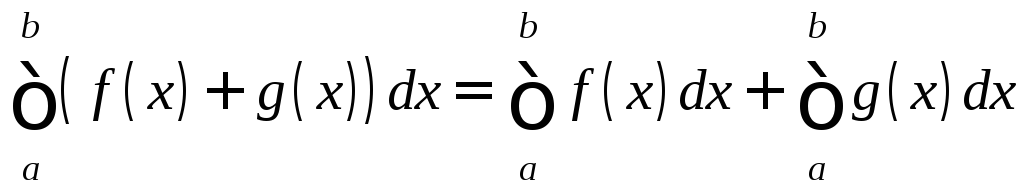 (3)
(3)
Доказательство.
![]() Выберем произвольное
разбиение
Выберем произвольное
разбиение
![]() отрезка [a;b]
и произвольно выберем точки ξk
отрезка [a;b]
и произвольно выберем точки ξk![]() [xk-1;xk].
[xk-1;xk].
 . (4)
. (4)
По
условию существуют
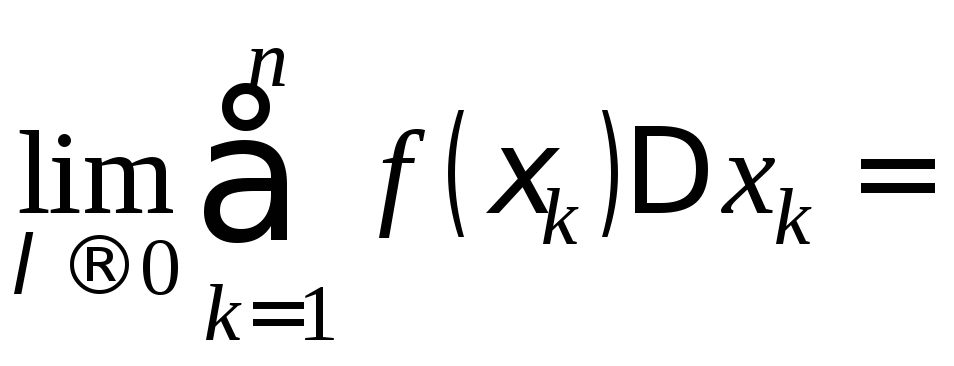
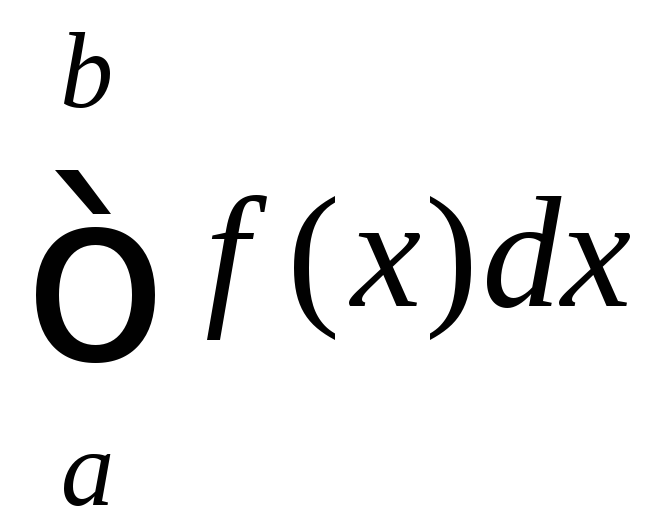 ,
,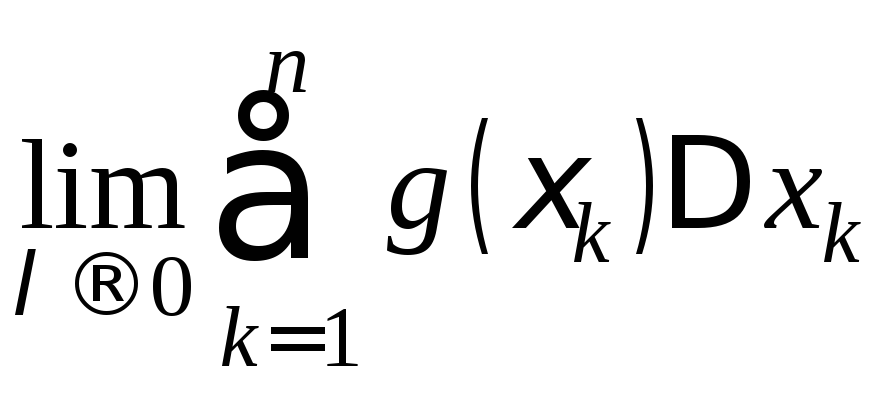
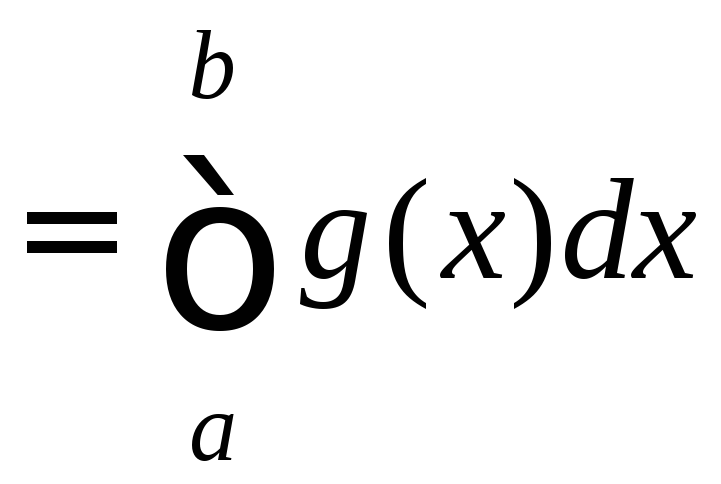 .
Следовательно, существует предел правой
части равенства (4), равный
.
Следовательно, существует предел правой
части равенства (4), равный
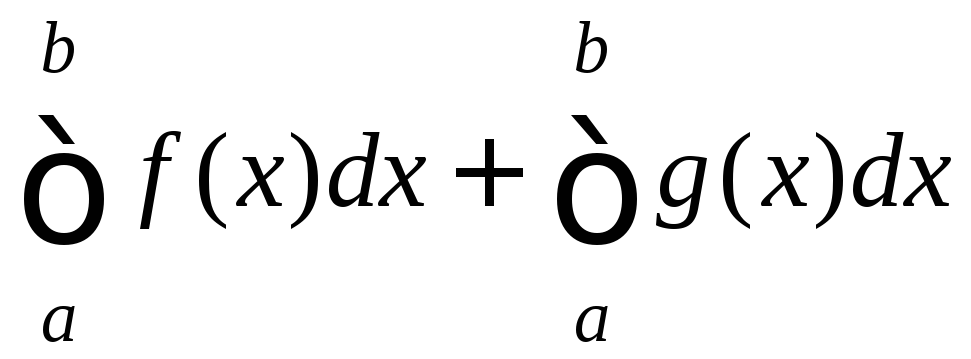 .
Значит, существует и предел левой части:
.
Значит, существует и предел левой части:
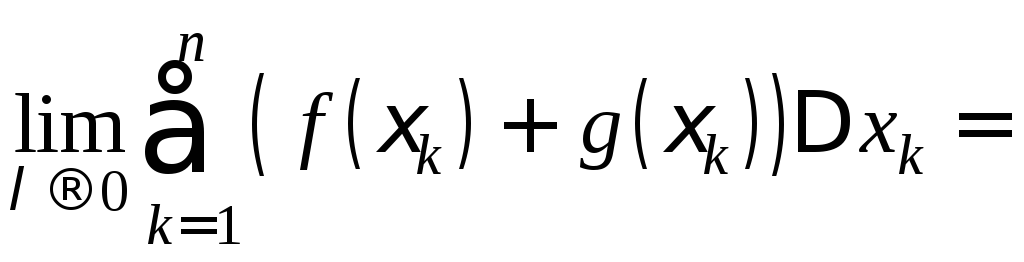
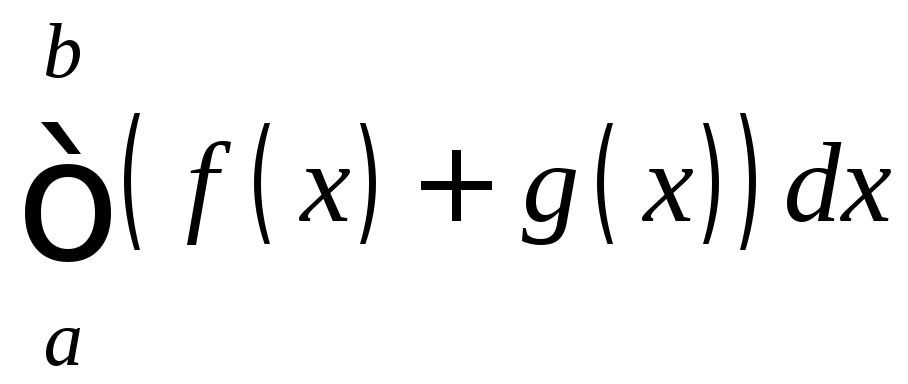 .
.
Переходя в (4) к
пределу, получим (3).
![]()
3.
Если f![]() R[a;b],
R[a;b],
![]() ,
то функцияcf
,
то функцияcf![]() R[a;b]
и
R[a;b]
и
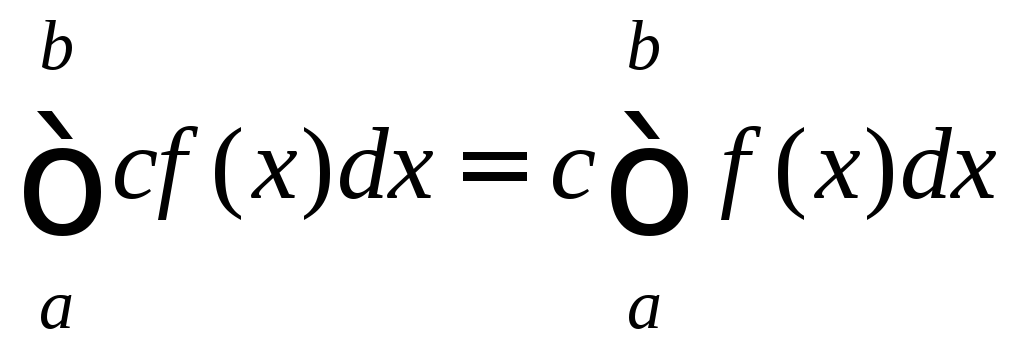 . (5)
. (5)
Доказательство.
![]() Выберем произвольное
разбиение
Выберем произвольное
разбиение
![]() отрезка [a;b]
и произвольно выберем точки ξk
отрезка [a;b]
и произвольно выберем точки ξk![]() [xk-1;xk].
Имеем
[xk-1;xk].
Имеем
 . (6)
. (6)
Т.к.
f![]() R[a;b],
то существует
R[a;b],
то существует
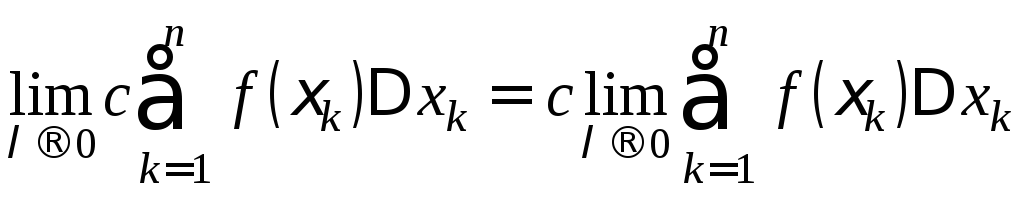
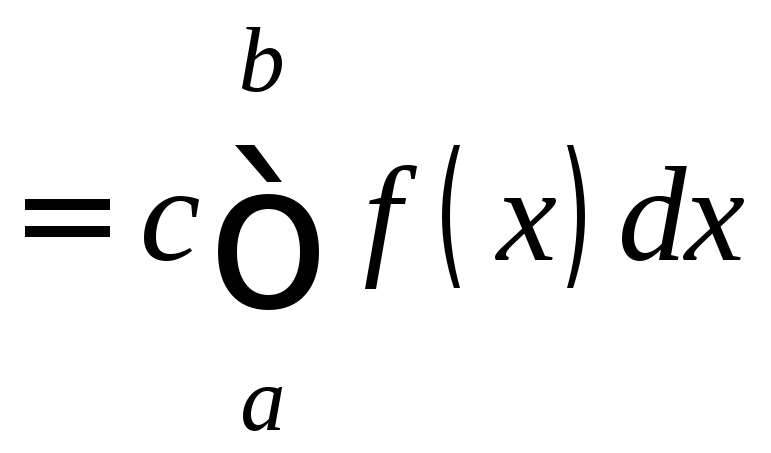 .
Следовательно, существует и предел
левой части равенства (5) и он равен
.
Следовательно, существует и предел
левой части равенства (5) и он равен
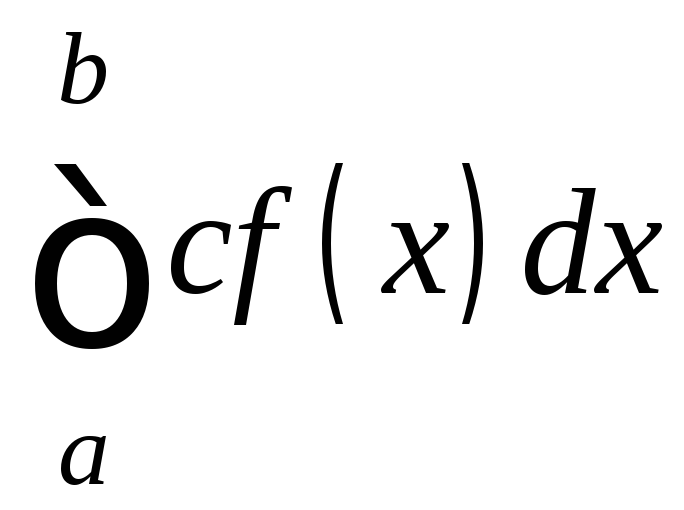 .
Переходя в (6) к пределу, получим (5).
.
Переходя в (6) к пределу, получим (5).![]()
Следствие. Если
f,
g![]() R[a;b]
и α,
β
R[a;b]
и α,
β![]() ,
то функция (αf+βg)
,
то функция (αf+βg)![]() R[a;b]
и
R[a;b]
и
 .
.
В частности,
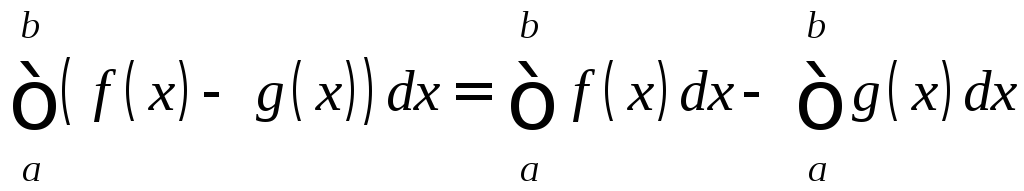 .
.
4.
Если f![]() R[a;b],
то f
R[a;b],
то f![]() R[α;β],
где [α;β]
R[α;β],
где [α;β]![]() [a;b].
[a;b].
Доказательство.
![]() Выберем произвольное
разбиение
Выберем произвольное
разбиение
![]() отрезка [a;b].
Т.к. f
отрезка [a;b].
Т.к. f![]() R[a;b],
то ε>0
δ>0,
такое, что для любого разбиения Т:
λ<δ
выполнено
R[a;b],
то ε>0
δ>0,
такое, что для любого разбиения Т:
λ<δ
выполнено
![]() .
ПустьТ:
λ<δ.
Присоединим
к Т
точки α
и β.
Получим разбиение Т′.
По свойству 2 верхних и нижних сумм
Дарбу
.
ПустьТ:
λ<δ.
Присоединим
к Т
точки α
и β.
Получим разбиение Т′.
По свойству 2 верхних и нижних сумм
Дарбу
![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]() . (7)
. (7)
Разбиение Т′
порождает разбиение Т
отрезка[α;β].
Следовательно, и для
![]() и
и![]() будет
выполняться (7), т.е.
будет
выполняться (7), т.е.![]() для любого разбиенияТ″:
λ<δ.
По необходимому и достаточному условию
интегрируемости это означает, что
f
для любого разбиенияТ″:
λ<δ.
По необходимому и достаточному условию
интегрируемости это означает, что
f![]() R[α;β].
R[α;β].
![]()
5. (Аддитивное
свойство интеграла) Пусть a<c<b
и f![]() R[a;b].
Тогда f
R[a;b].
Тогда f![]() R[a;с]
и f
R[a;с]
и f![]() R[с;b]
и
R[с;b]
и
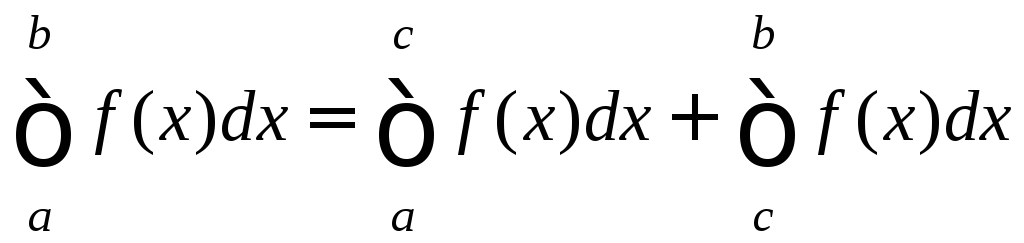 . (8)
. (8)
Доказательство.
![]()
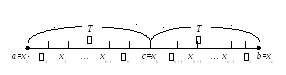 Интегрируемость
функции f
на [a;c]
и [c;b]
следует из свойства 4. Докажем (8). Пусть
Т
- произвольное разбиение отрезка [a;b].
Т.к. предел S(T,
ξk)
не зависит от способа разбиения [a;b],
то будем считать, что с
– одна из точек деления. Выберем
произвольно точки ξk
Интегрируемость
функции f
на [a;c]
и [c;b]
следует из свойства 4. Докажем (8). Пусть
Т
- произвольное разбиение отрезка [a;b].
Т.к. предел S(T,
ξk)
не зависит от способа разбиения [a;b],
то будем считать, что с
– одна из точек деления. Выберем
произвольно точки ξk![]() [xk-1;xk],
[xk-1;xk],
![]() .Т
порождает разбиение Т
с точками ξk
отрезка [a;c]
и Т
с точками ξk
отрезка [c;b],
причём Т=Т
.Т
порождает разбиение Т
с точками ξk
отрезка [a;c]
и Т
с точками ξk
отрезка [c;b],
причём Т=Т![]() Т,
{ξk}={ξk
}
Т,
{ξk}={ξk
}![]() {ξk
}. Тогда
{ξk
}. Тогда
S(T,ξk)=S(Т,ξk)+S(Т,ξk). (9)
Ясно, что λ(Т
)≤λ(Т),
λ(Т
)≤λ(Т).
Следовательно, если λ(Т)→0,
то λ(Т
)→0 и λ(Т
)→0. Переходя
к пределу в (9), получим (8).
![]()
Интегрирование неравенств
6. Если
f![]() R[a;b]
и
f(x)≥0
на
[a;b],
a<b,
то
R[a;b]
и
f(x)≥0
на
[a;b],
a<b,
то
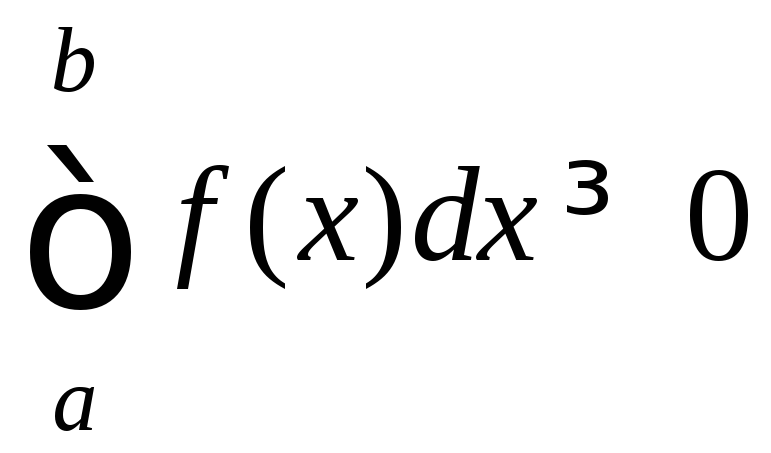 .Если
f(x)≤0,
a<b,
то
.Если
f(x)≤0,
a<b,
то
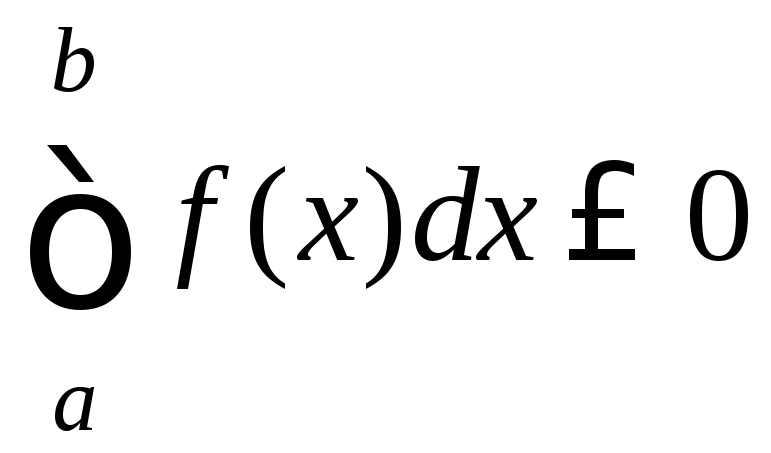 .
.
Доказательство.
![]() Пусть f(x)≥0
x
Пусть f(x)≥0
x![]() [a;b],
a<b.
Выберем произвольное разбиение
[a;b],
a<b.
Выберем произвольное разбиение
![]() отрезка [a;b]
и произвольно точки ξk
отрезка [a;b]
и произвольно точки ξk![]() [xk-1;xk],
[xk-1;xk],![]() .
Составим интегральную сумму
.
Составим интегральную сумму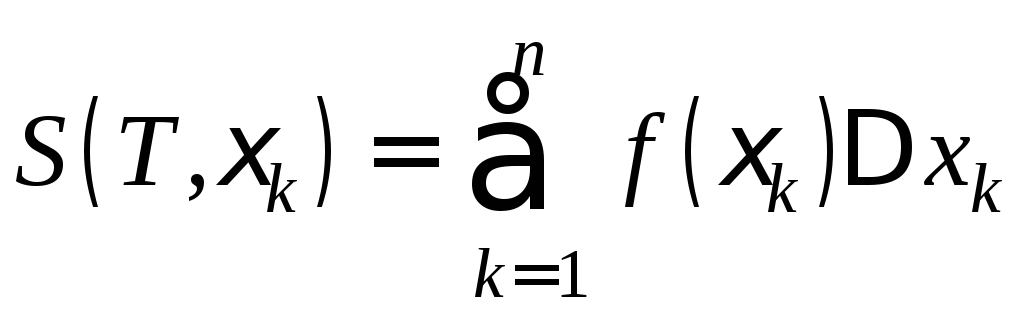 .
Т.к.f(ξk)≥0
и Δxk>0,
то S(T,ξk)≥0.
Переходя к пределу, получим
.
Т.к.f(ξk)≥0
и Δxk>0,
то S(T,ξk)≥0.
Переходя к пределу, получим
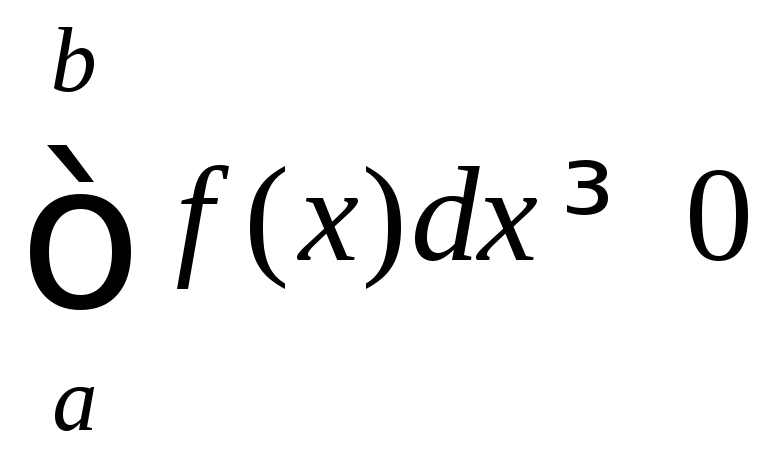 .
Случай f(x)≤0
– аналогично.
.
Случай f(x)≤0
– аналогично.
![]()
` Замечание 1.
Если f(x)≥0,
a>b,
то
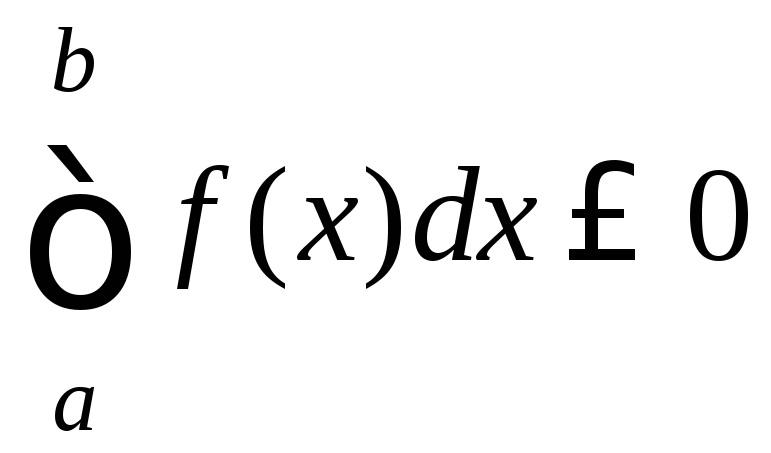 ;
;
если f(x)≤0,
a>b,
то
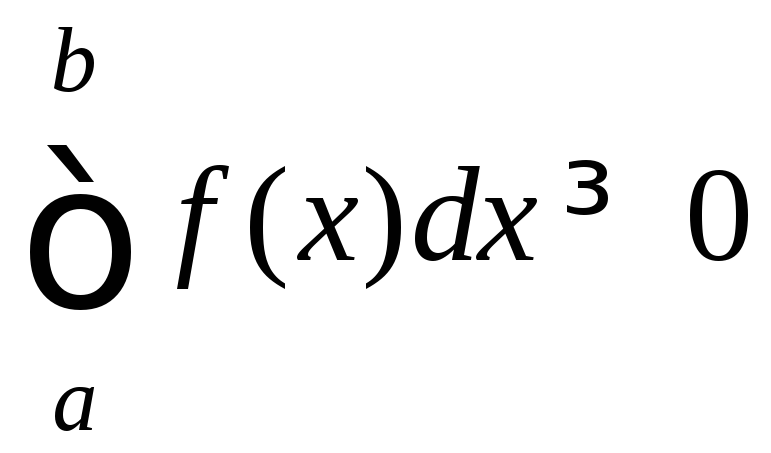 .
.
Замечание 2. Если
f(x)≥m,
a<b,
то
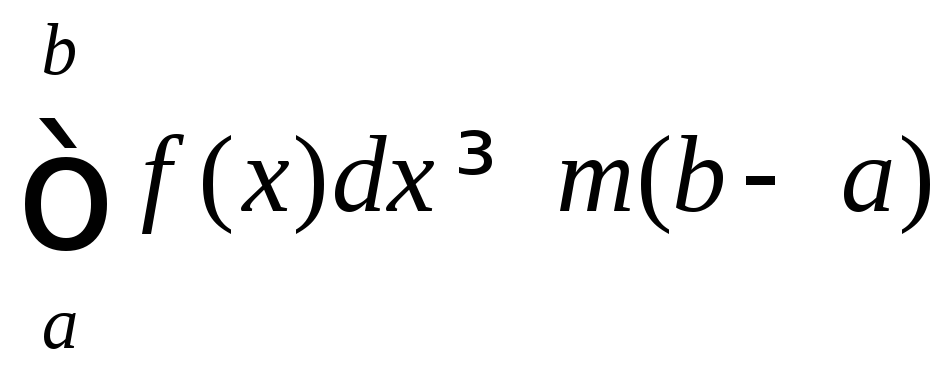 .
.
Доказательство.
![]() Действительно,
f(x)-m≥0,
a<b,
следовательно,
Действительно,
f(x)-m≥0,
a<b,
следовательно,
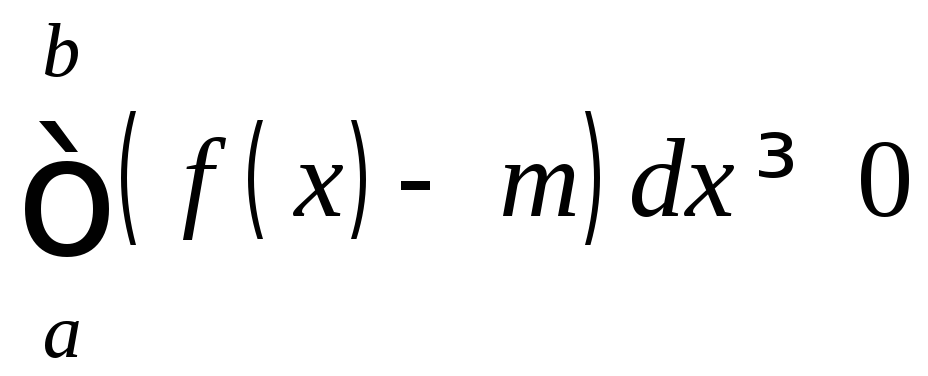 .
С другой стороны,
.
С другой стороны,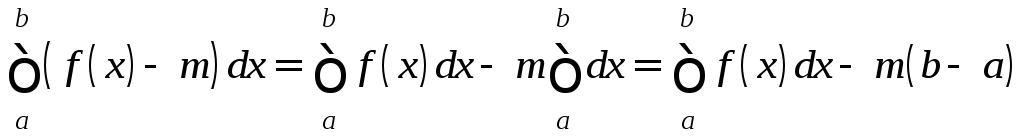 .
Следовательно,
.
Следовательно,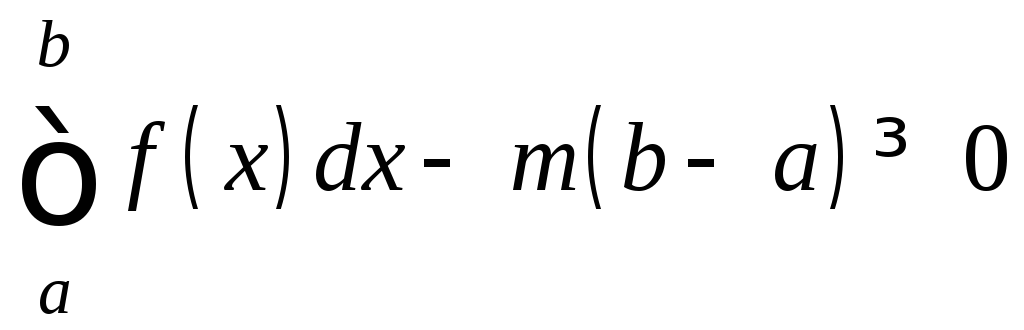 .
Отсюда
.
Отсюда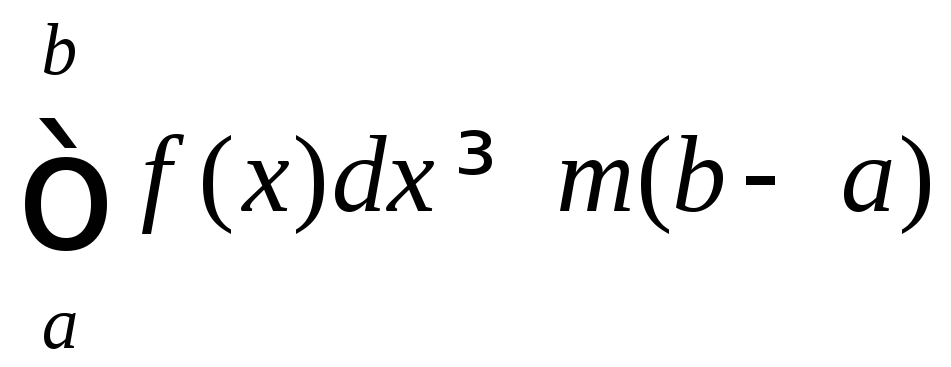 .
.
![]()
Замечание 3.
Пусть f
непрерывна и неотрицательна на [a;b].
Если f(x0)>0,
где x0![]() [a;b],
a<b,
то
[a;b],
a<b,
то
 .
.
Доказательство.
![]() Т.к. f
непрерывна на [a;b],
то f
непрерывна в x0
Т.к. f
непрерывна на [a;b],
то f
непрерывна в x0![]() [a;b].
Следовательно, ε>0
δ>0,
такое, что x
[a;b].
Следовательно, ε>0
δ>0,
такое, что x![]() (x0-δ;x0+δ)
выполнено |f(x)-f(x0)|<ε.
Возьмём
(x0-δ;x0+δ)
выполнено |f(x)-f(x0)|<ε.
Возьмём
![]() .
Обозначимα=x0-δ,
β=x0+δ.
Тогда x
.
Обозначимα=x0-δ,
β=x0+δ.
Тогда x![]() (α;β)
следует:
(α;β)
следует:
![]() ,
, ![]() .
.
Тогда
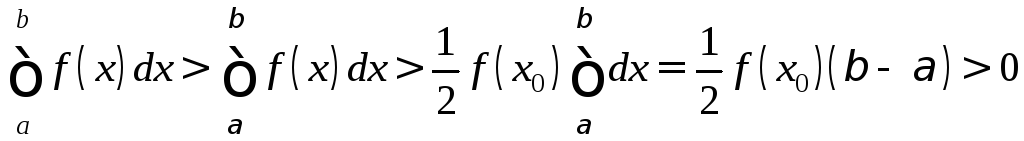 .
.![]()
7.
Пусть
f,
g![]() R[a;b],
a<b,
f(x)≤g(x)
x
R[a;b],
a<b,
f(x)≤g(x)
x![]() [a;b].
Тогда
[a;b].
Тогда
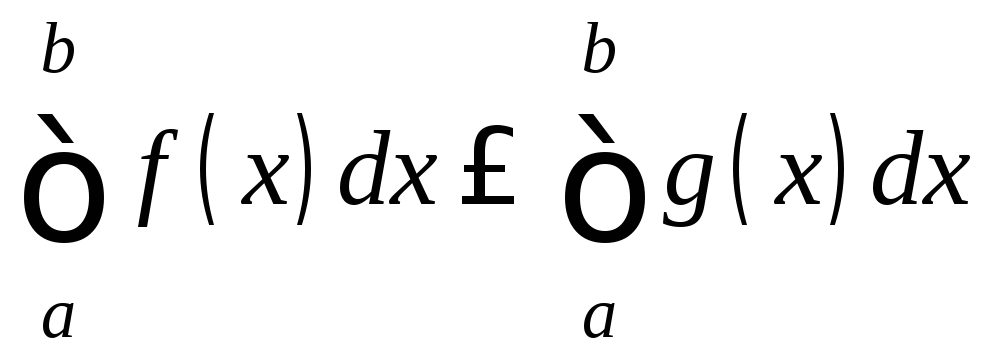 .
.
Доказательство.
![]() Применим свойство
6 к функции (g(x)-f(x))≥0:
Применим свойство
6 к функции (g(x)-f(x))≥0:
 .
С другой стороны,
.
С другой стороны,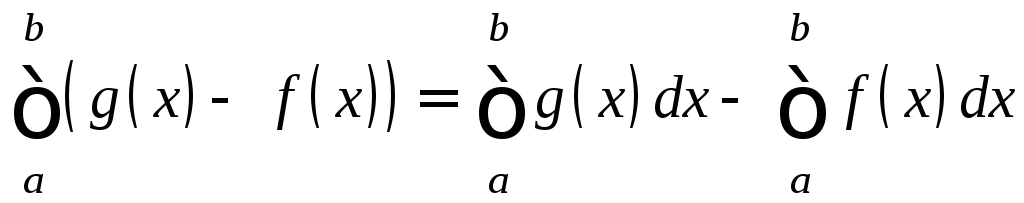 .
Следовательно,
.
Следовательно,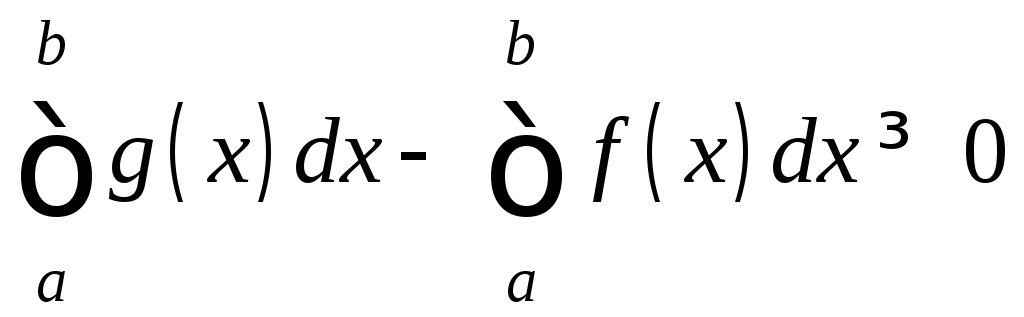 .
Отсюда
.
Отсюда
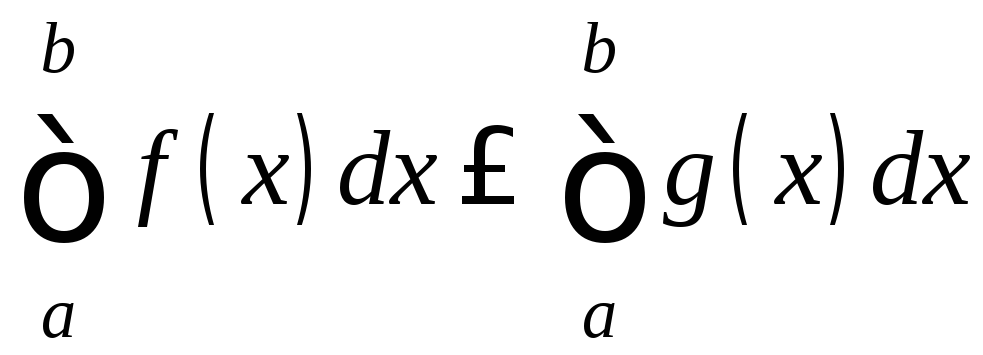 .
.
![]()
Замечание. Если
f,
g![]() C[a;b],
и в любой точке x0
C[a;b],
и в любой точке x0![]() [a;b]
выполнено неравенство f(x0)<g(x0),
то
[a;b]
выполнено неравенство f(x0)<g(x0),
то
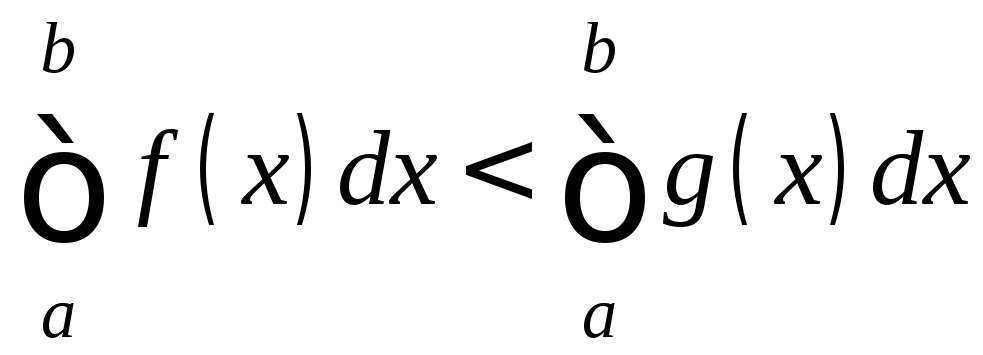 .
.
8. Если
f![]() R[a;b],
a<b,
то
|
f |
R[a;b],
a<b,
то
|
f |![]() R[a;b]
и
R[a;b]
и
 .(10)
.(10)
Доказательство.
![]() 1) Докажем, что |
f
|
1) Докажем, что |
f
|![]() R[a;b].
Выберем произвольное разбиение
R[a;b].
Выберем произвольное разбиение
![]() отрезка [a;b].
Обозначим
отрезка [a;b].
Обозначим
![]() ,
,![]() .Справедливо
неравенство
.Справедливо
неравенство
![]() (11)
(11)
(если mk
и Mk
одного знака, то
![]() ,
а если разного, то
,
а если разного, то
![]() ).
).
Умножим обе части
(11) на Δxk
и просуммируем по k
от 1 до n.
Получим
![]() .
Т.к. f
.
Т.к. f![]() R[a;b],
то по критерию интегрируемости ε>0
δ>0,
такое, что
R[a;b],
то по критерию интегрируемости ε>0
δ>0,
такое, что
![]() ,
еслиλ<δ.
Значит,
,
еслиλ<δ.
Значит,
![]() .
Поэтому | f
|
.
Поэтому | f
|![]() R[a;b].
R[a;b].
2) Докажем (10). В силу свойств модуля -| f(x)|≤ f(x)≤| f(x)|. Проинтегрируем по х на [a;b], используя свойство 7 и свойство 3:
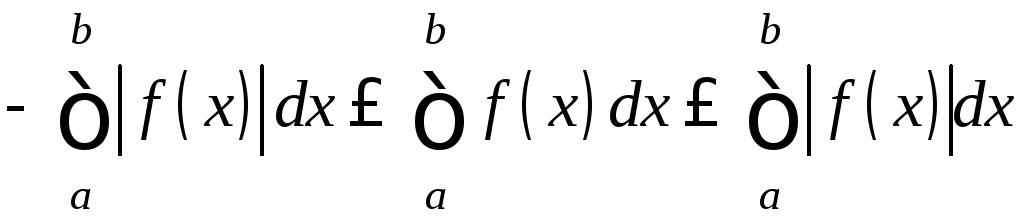 .
.
Следовательно,
(по свойству модуля),
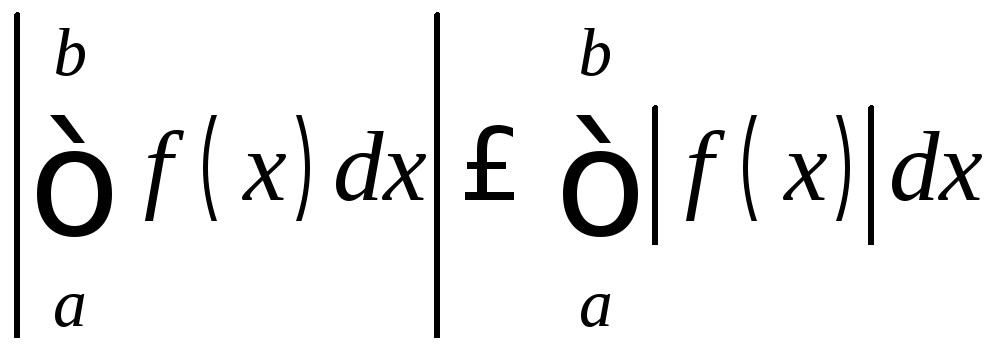 .
.
![]()
9. Теорема о среднем значении определённого интеграла.
Если f непрерывна на [a;b], то на [a;b] существует точка с, такая, что
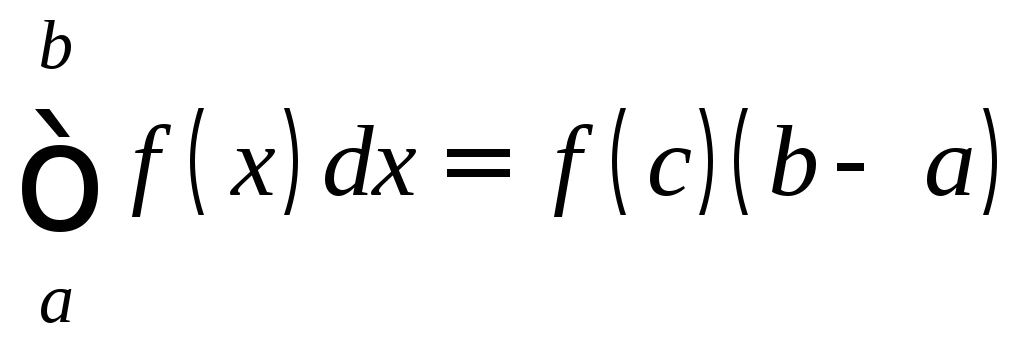 . (12)
. (12)
Доказательство.
![]() Т.к. f
Т.к. f![]() C[a;b],
то f
достигает на [a;b]
наименьшего и наибольшего значений m
и M
соответственно, т.е. x
C[a;b],
то f
достигает на [a;b]
наименьшего и наибольшего значений m
и M
соответственно, т.е. x![]() [a;b]
m≤f(x)≤M.
[a;b]
m≤f(x)≤M.
а) Пусть a<b.
По свойству
7
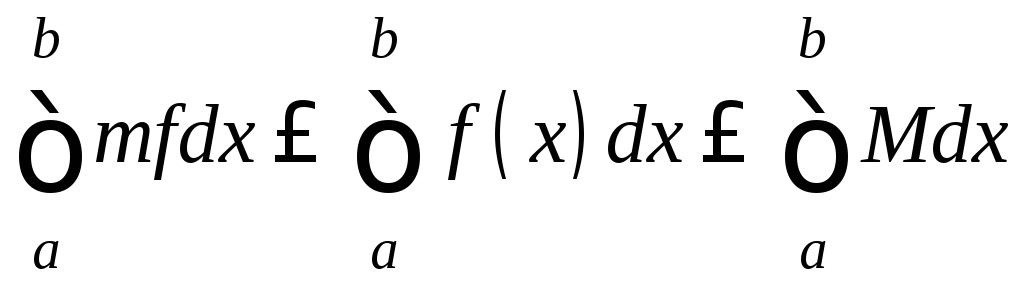 .
Следовательно,
.
Следовательно,
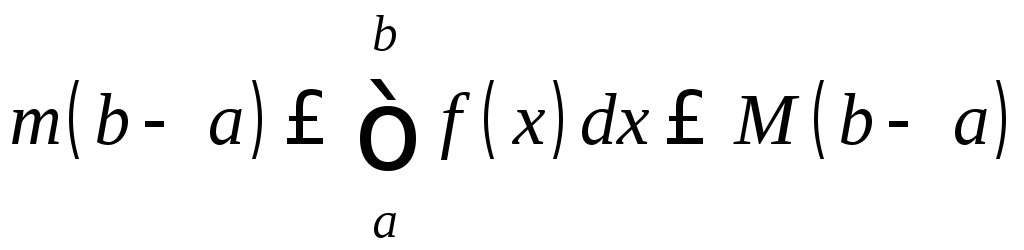 . (13)
. (13)
Отсюда
 .
Обозначим
.
Обозначим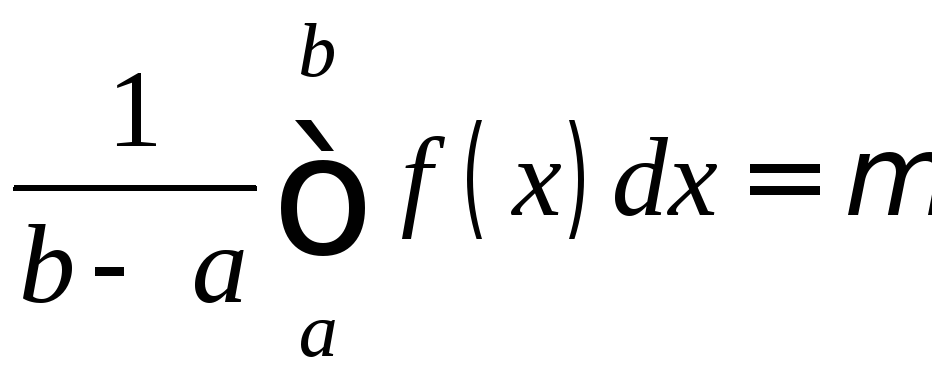 ,
где
,
где
![]() – число, заключённое между m
и M.
Т.к. f
непрерывна на [a;b],
то существует точка с
– число, заключённое между m
и M.
Т.к. f
непрерывна на [a;b],
то существует точка с![]() [a;b],
такая, что f(c)=μ.
Следовательно,
[a;b],
такая, что f(c)=μ.
Следовательно,
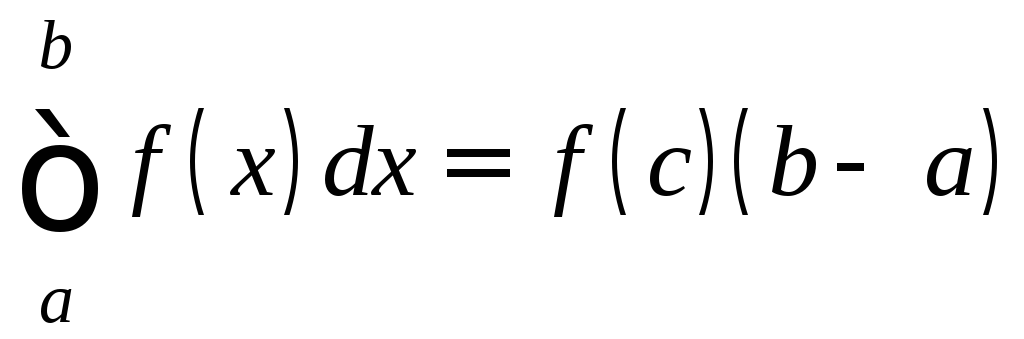 .
.
б) Пусть a>b.
Тогда
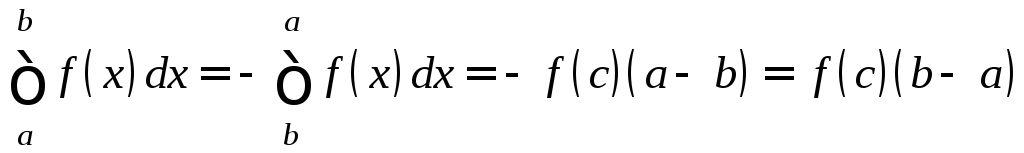 .
.![]()
