
- •Интегральное исчисление функций одной переменной
- •I. Неопределенный интеграл
- •§1. Первообразная
- •§2. Свойства неопределённого интеграла
- •§3. Основная таблица интегралов
- •§4. Основные методы интегрирования
- •I. Метод введения нового аргумента
- •II. Метод подстановки
- •III. Интегрирование по частям
- •§5. Интегрирование рациональных выражений
- •1. Основные понятия
- •2. Интегрирование простейших дробей.
- •1) ; 2); 3); 4) ,
- •3. Разложение правильной рациональной дроби на сумму простейших
- •4. Интегрирование рациональной функции
- •§6. Интегрирование иррациональных функций
- •§7. Интегрирование выражений, содержащих тригонометрические
- •II. Определенный интеграл
- •§1. Понятие определённого интеграла
- •§2. Нижние и верхние интегральные суммы
- •§3. Некоторые классы интегрируемых функций
- •1. Интегрируемость непрерывных функций.
- •2. Интегрируемость монотонной функции.
- •3. Интегрируемость функций, имеющих конечное число точек разрыва.
- •§4. Основные свойства определённого интеграла.
- •§5. Определённый интеграл с переменным верхним пределом. Существование первообразной функции. Формула Ньютона-Лейбница.
- •§6. Интегрирование по частям и замена переменной в определённом интеграле. Интегрирование чётных и нечётных функций.
§6. Интегрирование иррациональных функций
Через R(x;y) будем обозначать рациональную функцию от двух аргументов x и y, т.е. функцию, которая получена из x и y и некоторых постоянных с помощью конечного числа рациональных операций: умножения, сложения, вычитания, деления.
Например, 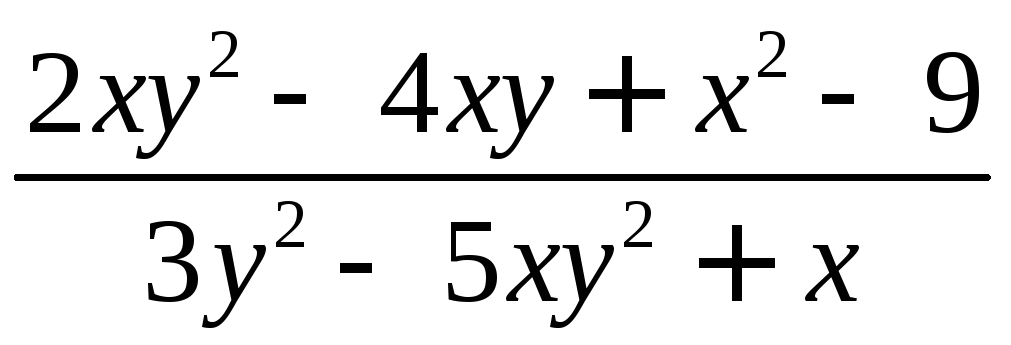 -
рациональная функция отx
и y;
-
рациональная функция отx
и y;
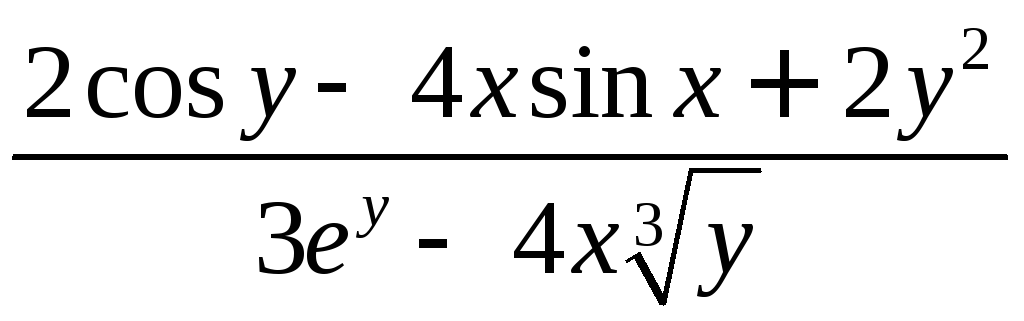 -
не является рациональной функцией,
т.к. содержит
-
не является рациональной функцией,
т.к. содержит
![]() .
.
Справедливо утверждение: если R(x;y) – рациональная функция от x и y, а R1(t), R2(t), R3(t)- рациональные функции от переменной t, то R(R1(t),R2(t))∙R3(t)- рациональная функция от t.
I.
Интегралы вида
![]()
 (1)
(1)
R-
рациональная функция от x
и
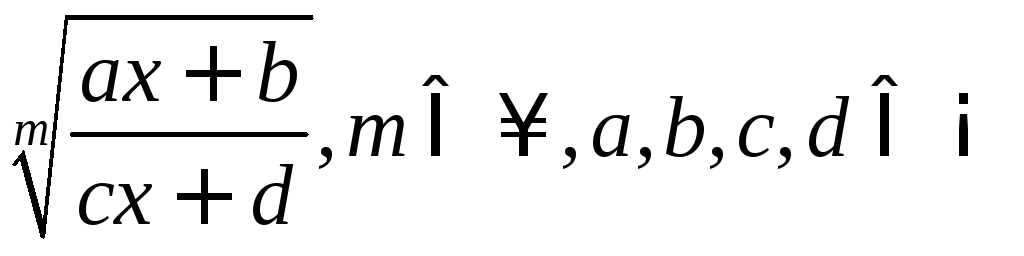 ,
и
,
и![]()
Введём подстановку
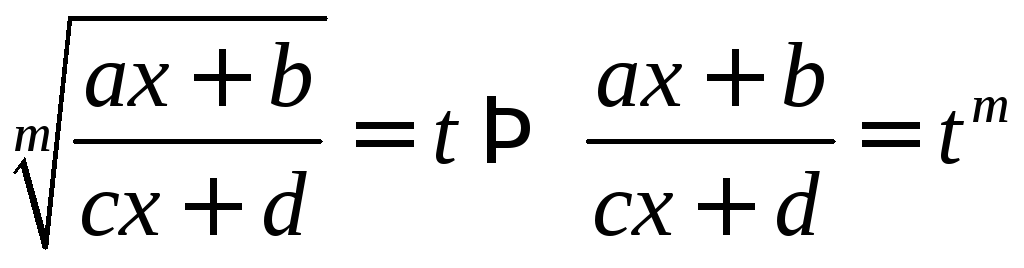 – линейное уравнение относительноx.
Следовательно,
– линейное уравнение относительноx.
Следовательно,
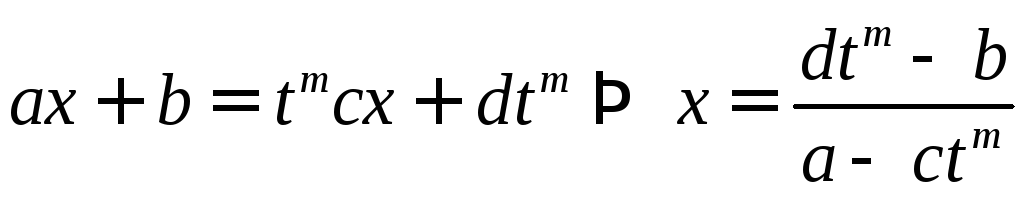 - рациональная функция отt,
обозначим её R1(t),
тогда dx=(R1(t))dt=R2(t)dt
и, следовательно, x
и dx
рационально выражаются через t.
Получим
- рациональная функция отt,
обозначим её R1(t),
тогда dx=(R1(t))dt=R2(t)dt
и, следовательно, x
и dx
рационально выражаются через t.
Получим
![]() .
.
Значит, 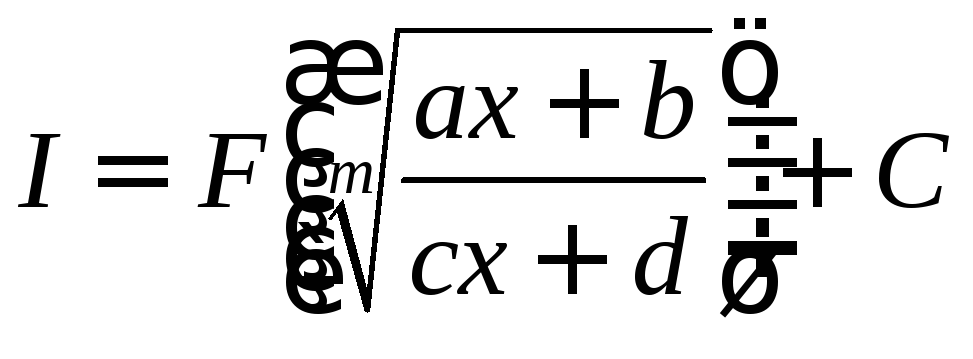 .
.
Частный случай
интеграла
(1): c=0,
d=1.
Получим
![]() ,
следовательно,
,
следовательно,![]() .
.
К интегралу (1) приводят интегралы более общего вида:
 . (2)
. (2)
(2) приводится к
(1) с помощью подстановки
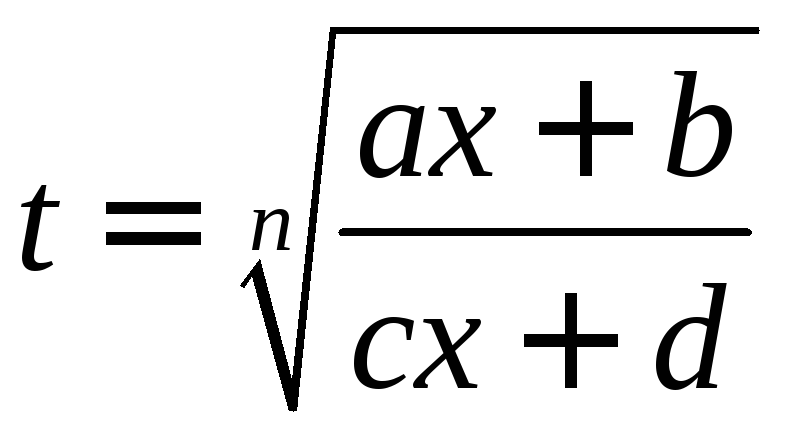 ,
гдеn
- наименьшее общее кратное показателей
m1,…,
mk
.
,
гдеn
- наименьшее общее кратное показателей
m1,…,
mk
.
Пример 1.
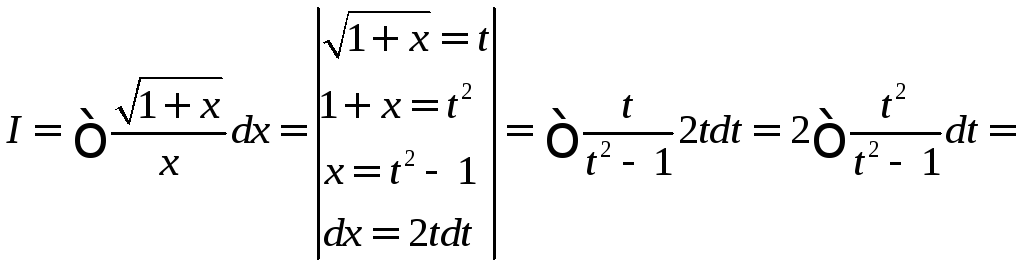
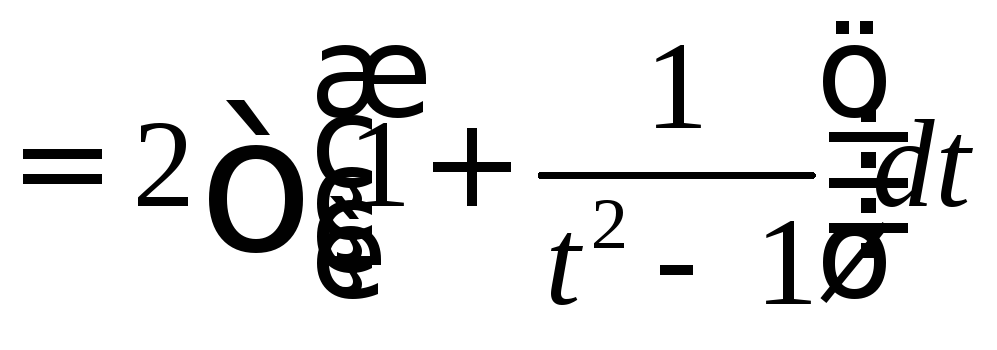
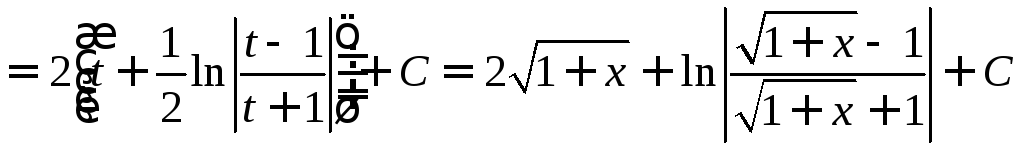 .
.
II.
Интегралы вида
![]() (3)
(3)
вычисляются в общем случае с помощью подстановок Эйлера.
Частные случаи (некоторые иррациональности)
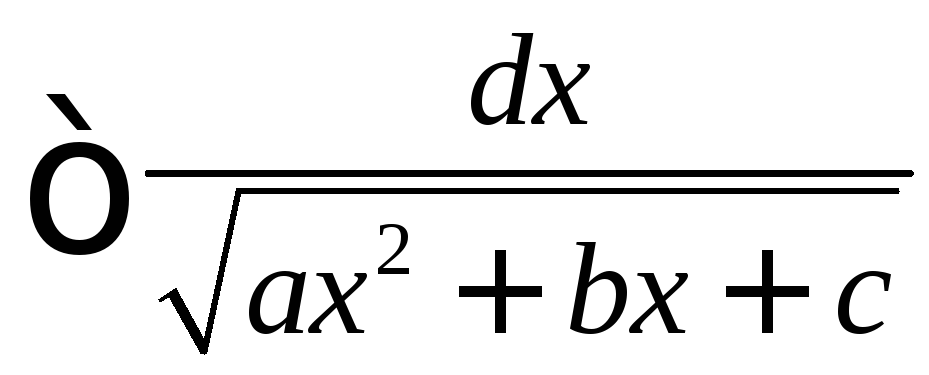 .
С помощью выделения полного квадрата
в подкоренном выражении сводится к
табличным интегралам.
.
С помощью выделения полного квадрата
в подкоренном выражении сводится к
табличным интегралам.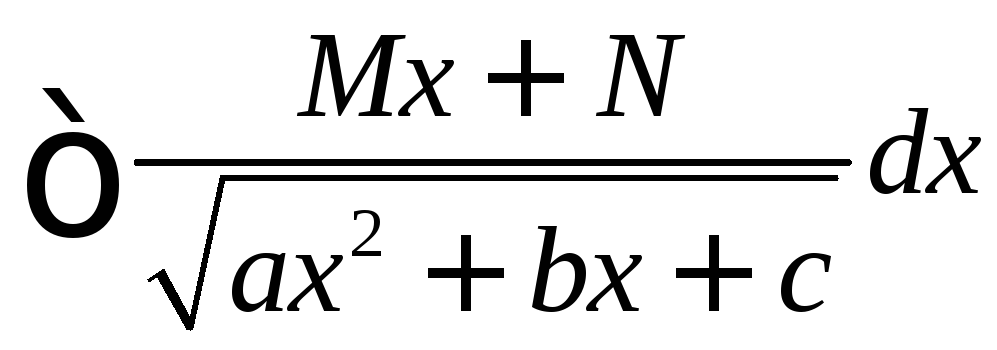 .
В числителе выделяем производную
подкоренного выражения. Поделив
почленно, получим табличный интеграл
и интеграл предыдущего типа.
.
В числителе выделяем производную
подкоренного выражения. Поделив
почленно, получим табличный интеграл
и интеграл предыдущего типа.
Пример 2.
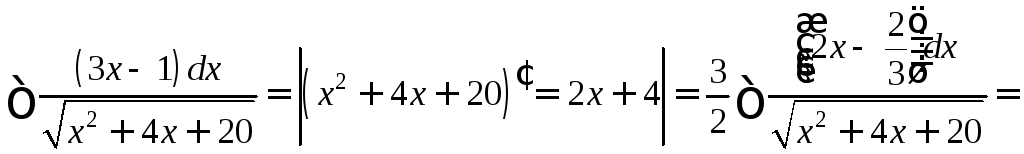
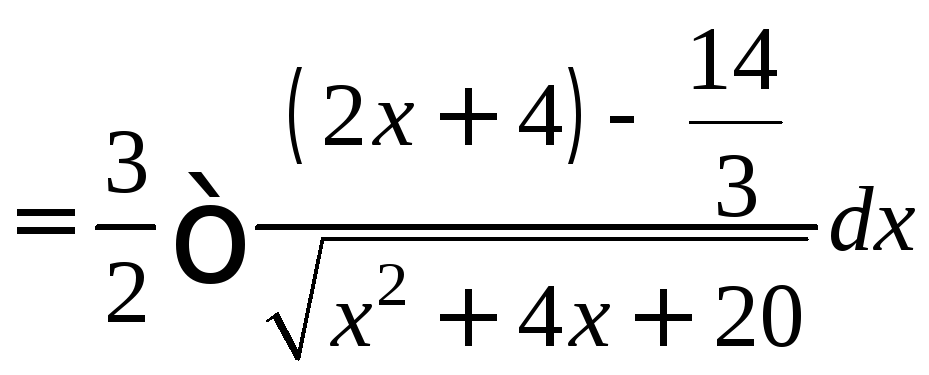
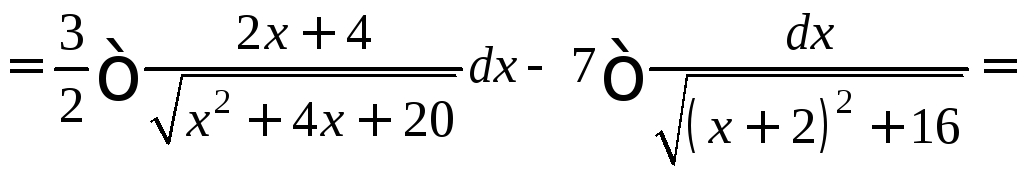
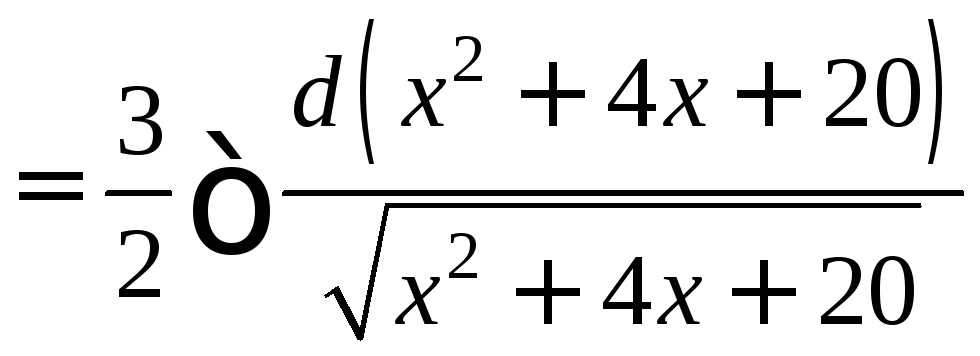

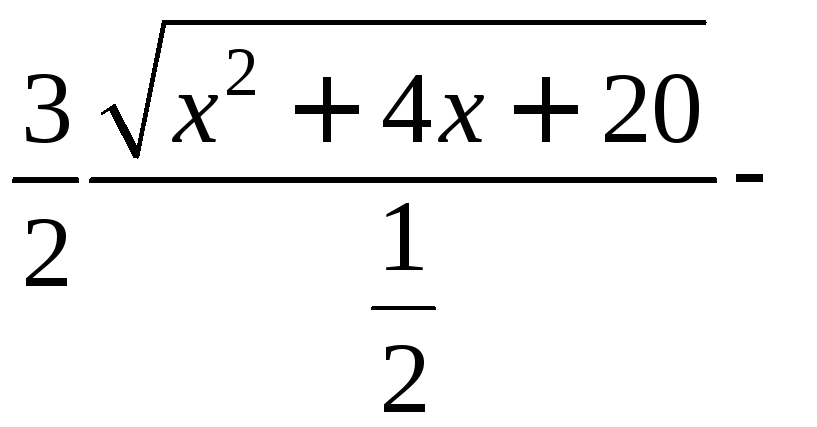
![]()
![]() .
.
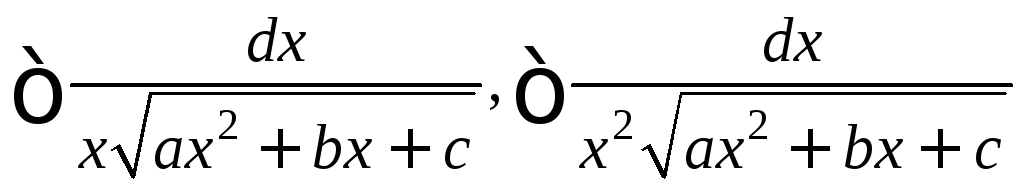 -
подстановка
-
подстановка
 .
.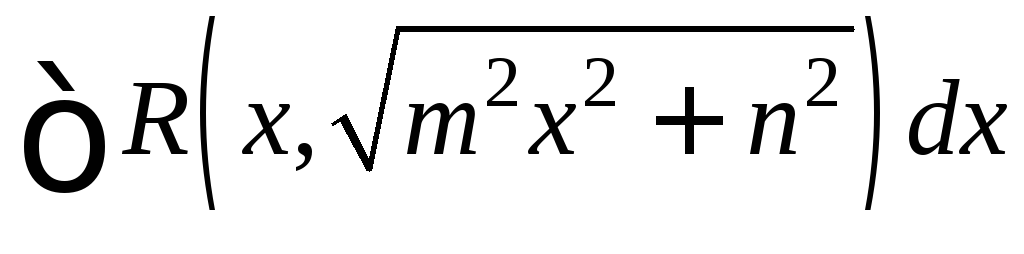 .
.
Применяется тригонометрическая подстановка mx=ntgt или mx=nctgt.
Частный случай

Применяется
тригонометрическая подстановка
![]() (
(![]() )
)
Частный случай
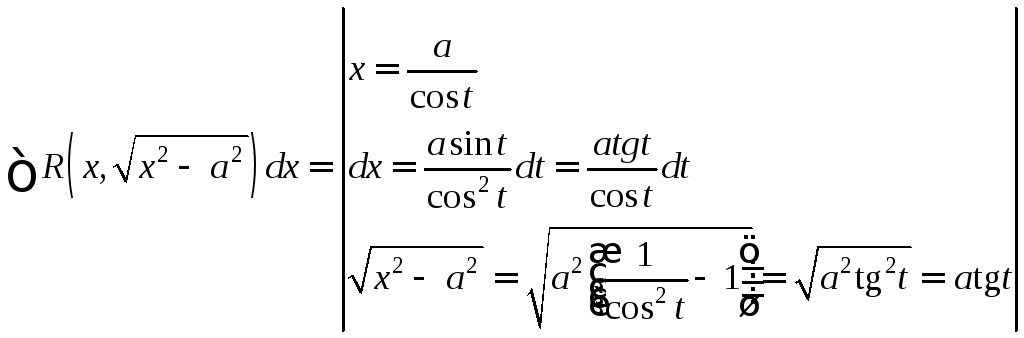
Применяется тригонометрическая подстановка mx=nsint (mx=ncost)
Частный случай
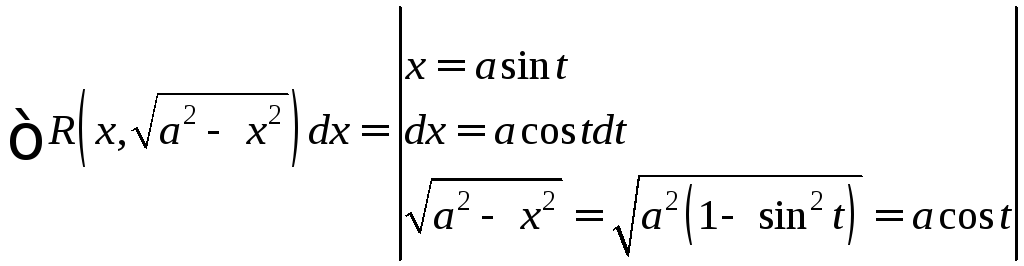
§7. Интегрирование выражений, содержащих тригонометрические
и показательную функции
I.![]()
Подстановка t=![]() (-π<x<π)
приводит такой интеграл к интегралу
от рациональной функции. Выразим sinx,
cosx,
x
и dx
через t:
(-π<x<π)
приводит такой интеграл к интегралу
от рациональной функции. Выразим sinx,
cosx,
x
и dx
через t:
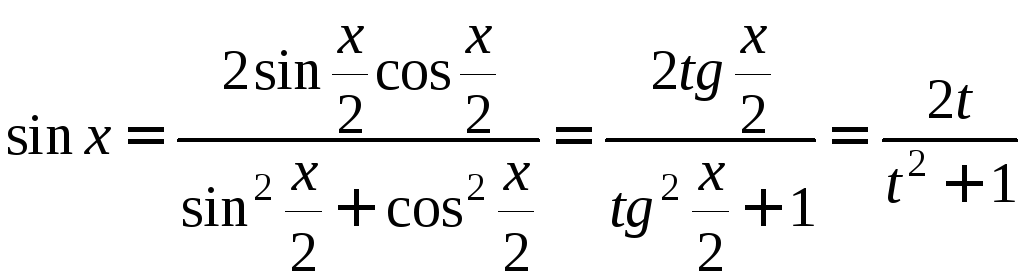 ;
;
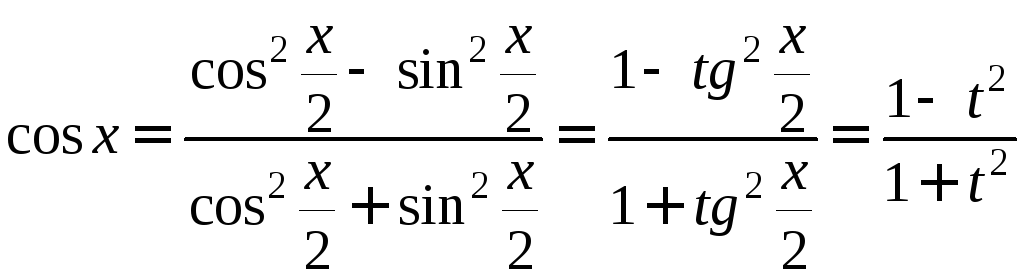 ;
;
![]() .
.
sinx, cosx, dx рационально выражаются через t. Следовательно,
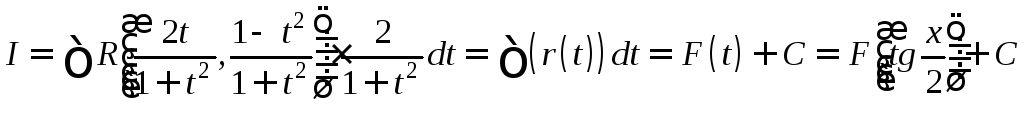 .
.
Данная подстановка называется универсальной тригонометрической подстановкой. Она часто приводит к громоздким вычислениям. Поэтому на практике её стараются избежать. Рассмотрим частные случаи, когда можно обойтись без универсальной тригонометрической подстановки.
II.Частные случаи
а) R(-sinx, cosx)=-R(sinx, cosx).
Если подынтегральная функция меняет знак при замене sinx на –sinx, то применяется подстановка cosx=t.
б) R(sinx, -cosx)=-R(sinx, cosx).
Если подынтегральная функция меняет знак при замене cosx на –cosx, то применяется подстановка sinx=t.
в) R(-sinx, -cosx)=R(sinx, cosx).
Если подынтегральная функция не меняется при изменении знаков у cosx и sinx, то применяется подстановка tgx=t (ctgx=t).
III.![]()
1. Если n-нечётно, то применяется подстановка sinx=t.
Пусть n=2k+1, тогда
![]()
![]() .
.
2. Если m=2k+1-нечётное, то применяется подстановка cosx=t.
Пример.
![]()
![]()
![]()
![]()
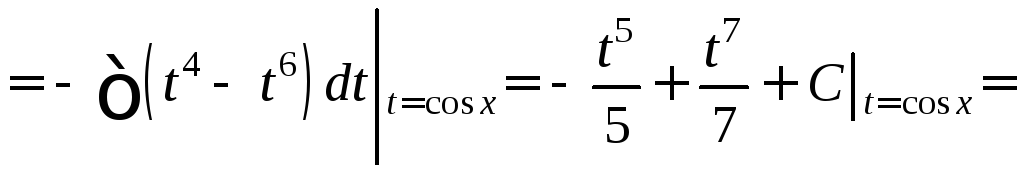
![]()
3. m+n=0
a) m>0
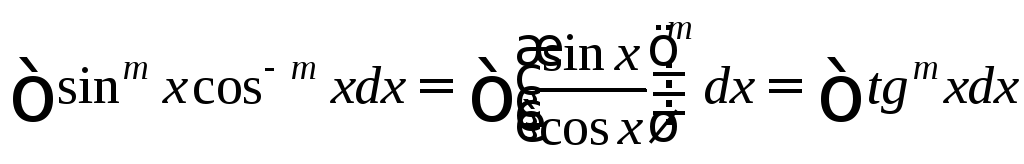 .
Подстановка t=tgx.
.
Подстановка t=tgx.
б) n>0
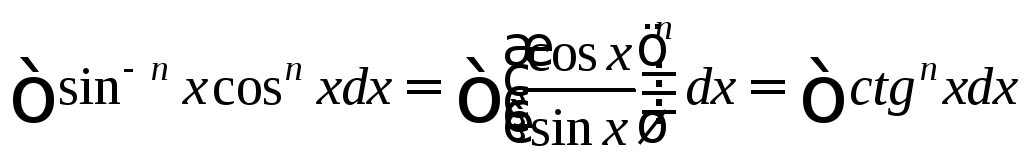 .
Подстановка t=ctgx.
.
Подстановка t=ctgx.
4.
m+n=-2k,
k![]()
a) m>0
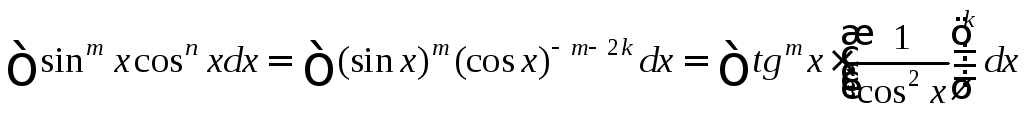 .
.
Подстановка t=tgx.
б) n>0
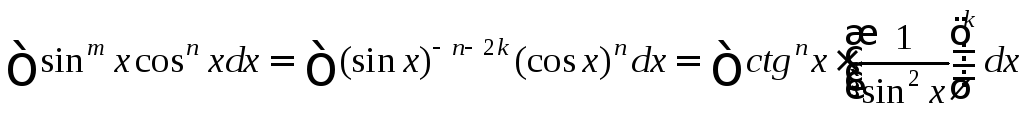 .
.
Подстановка t=ctgx.
5. m, n-чётные неотрицательные числа. Применяются формулы понижения степени:
![]() .
.
6. m, n-чётные, хотя бы одно из них неотрицательно. Применяется подстановка t=tgx или t=ctgx
IV.
![]() .
Подстановкаt=tgх.
.
Подстановкаt=tgх.
![]() .
Подстановка t=ctgx.
.
Подстановка t=ctgx.
V. a)
![]()
б)
![]()
в)
![]()
Применим формулы: а)
![]()
![]()
б)
![]()
![]()
в)
![]()
![]()
VI.
![]() .
Подстановкаt=ex.
Отсюда x=lnt.
Следовательно,
.
Подстановкаt=ex.
Отсюда x=lnt.
Следовательно,
![]() .
Тогда,
.
Тогда,
![]() -интеграл от рациональной функции отt.
-интеграл от рациональной функции отt.
