
- •Оглавление
- •Источники погрешностей при вычислениях по формулам.
- •1.1.Абсолютная и относительная погрешности. Оценки погрешностей
- •1.2. Границы значений числовых величин
- •1.3. Запись приближенных значений. Верные знаки
- •1.4. Округление. Погрешность округления. Первое правило подсчета верных знаков
- •Первое правило верных знаков
- •1.5. Линейные оценки погрешностей.
- •Линейные оценки погрешностей для функций нескольких переменных.
- •1.6. Метод границ
- •1.7. Правила подсчета верных знаков.
- •Контрольные вопросы
- •Литература
- •Тема 2. Численные методы решения уравнений с одним неизвестным
- •2.1. Постановка задачи. Метод последовательных приближений. Отделение корней
- •Отделение корней
- •Общая характеристика итерационных методов решения уравнений.
- •2.2. Метод половинного деления
- •2.3. Метод простой итерации
- •2.4. Метод касательных
- •2.5. Метод секущих
- •Оценка погрешности методов.
- •2.6. Комбинированный метод секущих и касательных
- •Контрольные вопросы
- •Литература
- •Тема 3. Численные методы решения систем уравнений
- •3.1. Постановка задачи
- •Общая характеристика численных методов решения систем линейных уравнений
- •3.2. Метод Гаусса
- •3.3. Метод простой итерации решения систем линейных уравнений
- •Контрольные вопросы
- •Литература
- •Тема 4. Интерполирование функций
- •4.1. Постановка задачи
- •4.2. Интерполяционный многочлен Лагранжа
- •Оценка погрешности интерполяционных формул
- •Контрольные вопросы
- •Литература
- •Тема 5. Наилучшее среднеквадратическое приближение
- •5.1. Аппроксимация функций методом наименьших квадратов
- •Нахождение приближающей функции в виде квадратного трехчлена
- •Контрольные вопросы
- •Литература
- •Тема 6. Численное интегрирование
- •6.1. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона–Котеса
- •Формулы прямоугольников
- •Формула трапеций
- •Формула Симпсона (парабол)
- •6.2. Принцип Рунге оценки погрешностей
- •6.3. Статистический метод вычисления интегралов
- •I схема метода Монте–Карло
- •II схема метода Монте - Карло
- •Нахождение первообразной
- •Контрольные вопросы
- •Литература
- •Глоссарий
2.2. Метод половинного деления
 Пусть
уравнение f(x)=0
имеет на отрезке [a,
b]
единственный корень, причем функция
f(x)
на этом отрезке непрерывна. Разделим
[a,
b]
пополам точкой c=(a+b)/2.
Если f(c)
Пусть
уравнение f(x)=0
имеет на отрезке [a,
b]
единственный корень, причем функция
f(x)
на этом отрезке непрерывна. Разделим
[a,
b]
пополам точкой c=(a+b)/2.
Если f(c)![]() ,
то возможны 2 случая: функция имеет
разные знаки на концах отрезка [a,
c],
либо на концах отрезка [c,
b].
,
то возможны 2 случая: функция имеет
разные знаки на концах отрезка [a,
c],
либо на концах отрезка [c,
b].
Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.
Сформулируем достаточные условия сходимости этого метода:
Теорема 3. Если
функция f(x) непрерывна на [a, b];
f(a)f(b)<0;
уравнение (1) имеет на [a, b] единственный корень xc
члены итерационной последовательности вычисляется по формуле:
 ,n
,n N,
где a1=a,
b1=b
N,
где a1=a,
b1=b

 ,
,
Тогда
 (итерационная
последовательность сходится к корню
уравнения)
(итерационная
последовательность сходится к корню
уравнения) n
n (оценка погрешности приближения).
(оценка погрешности приближения).
2.3. Метод простой итерации
Пусть [a, b]- отрезок, содержащий корень уравнения f(x)=0 (1). Заменим уравнение (1) равносильным ему уравнением: x=φ(x) (2) на [a, b].
Построим итерационную
последовательность {xn}
с помощью формулы xn+1=φ(xn),
n=0,
1, 2, … x0-
грубое приближение к корню xc,
x0![]() .Последовательность
x0,
x1,…,xn,…
может сходиться, так и расходиться. Если
последовательность сходиться, а функция
φ(x)
непрерывна, то предел последовательности
{xn}
является корнем уравнения (1).
.Последовательность
x0,
x1,…,xn,…
может сходиться, так и расходиться. Если
последовательность сходиться, а функция
φ(x)
непрерывна, то предел последовательности
{xn}
является корнем уравнения (1).
Теорема 4. Пусть
φ(x) определена и дифференцируема на [a, b];
 φ(x)
[a,
b];
φ(x)
[a,
b]; что
что


Тогда
 xn+1=φ(xn),
n=0,
1, 2,
xn+1=φ(xn),
n=0,
1, 2,
 ,
гдеxc-
корень уравнения (2), и причем единственный.
,
гдеxc-
корень уравнения (2), и причем единственный. ;
;
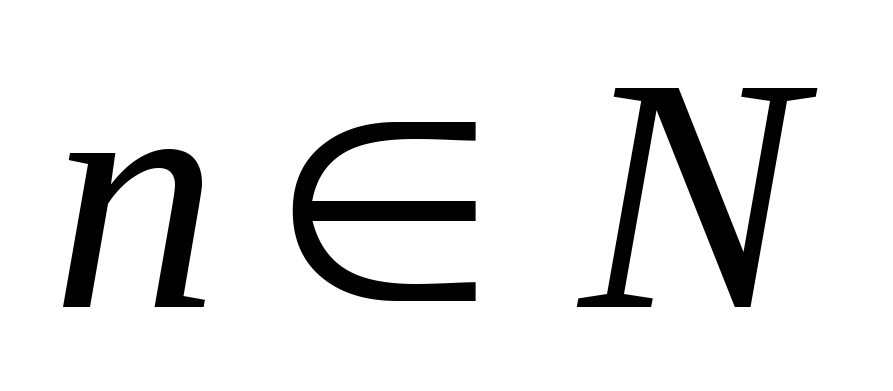 .
.
Доказательство. Построим интеграционную последовательность {xn} с любым начальным значением x0є [a,b]. В силу условия (2) теоремы все члены последовательности находятся в отрезке [a, b].
Рассмотрим два последовательных приближения xn=φ(xn-1) и xn+1= φ(xn). По теореме Лагранжа о конечных приращениях
xn+1-xn=φ(xn)-φ(xn-1)=φ’(c) (xn- xn-1), c є[xn-1; xn]
Перейдя к модулям и принимая во внимание условие (3) теоремы, получим: | xn+1-xn|= | φ’(c)| | xn- xn-1|≤q| xn- xn-1|, т.е. | xn+1-xn|≤q| xn- xn-1|. При n=1,2,… будем иметь: | x2-x1|≤q| x1- x0|, | x3-x2|≤q | x2- x1|≤q2| x1- x0|, … | xn+1-xn|≤qn | x1- x0|.
Рассмотрим ряд: x0+(x1-x0)+( x2-x1)+…+( xn-xn-1)+… (*).
Сразу заметим, что Sn+1=xn. Члены ряда (*), начиная со второго , не превосходят по модулю соответствующих членов ряда:
|x1-x0|+q|x1-x0|+q2|x1-x0|+…+qn|x1-x0|+… (**)
Но ряд (**) сходится
как геометрическая прогрессия со
знаменателем q<1,
следовательно, ряд (*) абсолютно сходится
по теореме сравнения. Поэтому,
![]()
Покажем, что xc-
корень уравнения x=φ(x).
Имеем: xn+1=φ(xn),
n=0,1,2,..
Т.к. φ- дифференцируема, то она непрерывна
на[a,
b],
следовательно, можно перейти к пределу:

![]() xc=φ(xc0),
т.е. xc-
корень уравнения (2). Допустим, что
xc=φ(xc0),
т.е. xc-
корень уравнения (2). Допустим, что
![]() и
и![]()
|xc-![]() |=|
|=|![]() |
|![]()
Получим противоречие,
следовательно,
![]()
Оценим погрешность: |xn-xc|=|φ(xn-1)-φ(xc)|≤q| xn-1- xc|≤qn|x0-xc|≤ qn|b-a|
|xn-1-xc|=|(
xn-1-xn)+(xn-xc)|≤|
xn-1-xn|+
|xn-xc|≤|
xn-1-xn|+q|
xn-1-xc|![]()
| xn-1-xc|≤![]() .
С другой стороны: |xn-xc|≤q|xn-1-xc|
.
С другой стороны: |xn-xc|≤q|xn-1-xc|
![]() |xn-1-xc|≥
|xn-1-xc|≥![]()
![]() ≤|xn-1-xc|≤
≤|xn-1-xc|≤![]() ,
|xn-xc|≤
,
|xn-xc|≤![]()
Практически уравнение f(x)=0 может быть приведено к виду x=φ(x) многими способами, однако это следует сделать так, чтобы для функции φ(x) выполнялись условия (1)- (3) теоремы.
На практике часто условие (2) не проверяют, а используют следующую теорему:
Теорема 5. Пусть:
[a, b] содержит единственный корень уравнения (2);
φ(x) дифференцируема на [a, b];
 ,
такое, что
,
такое, что
 |φ’(x)|≤q.
|φ’(x)|≤q.
Тогда итерационная последовательность xn+1=φ(xn), n=0, 1, 2,… сходится к корню xc хотя бы для одного из натуральных приближений x0=a или х0=b и справедливы оценки погрешности предыдущей теоремы.
Для того, чтобы
выполнялось условие (3), в некоторых
случаях помимо обычных преобразованиях
(f(x)=0
![]() x=x+f(x))
полезно иметь в виду следующие специальные
приемы:
x=x+f(x))
полезно иметь в виду следующие специальные
приемы:
1 Уравнение f(x)=0 преобразуем к виду: х=x-mf(x), где m=const, m≠0. В этом случае φ(x)=x-mf(x) и φ’(x)=1-mf’(x). Для того чтобы |φ’(x)|=|1-mf’(x)|≤q<1, достаточно подобрать m так (если, конечно, это возможно), чтобы для всех x из отрезка [a, b] значением выражения mf’(x) была положительная правильная дробь.
2
Пусть уравнение f(x)=0
записано в виде x=φ(x).
Однако при исследовании функции φ(x)
на [a,
b],
оказалось, что
![]() x
x![]() [a,
b]
|φ’(x)|>1.
Тогда вместо функции y=
φ(x)
рассмотрим функцию x=g(у),
обратную для φ(x).
Будем теперь решать уравнение y=g(у)
(или, в старых обозначениях, x=g(x)).
По свойству производных обратных функций
теперь на [a,
b]
будет иметь место: |g’(x)|=
[a,
b]
|φ’(x)|>1.
Тогда вместо функции y=
φ(x)
рассмотрим функцию x=g(у),
обратную для φ(x).
Будем теперь решать уравнение y=g(у)
(или, в старых обозначениях, x=g(x)).
По свойству производных обратных функций
теперь на [a,
b]
будет иметь место: |g’(x)|=![]() .
Так что для уравнения x=g(x),
равносильного искомому условие (3)
теоремы оказалось выполненным.
.
Так что для уравнения x=g(x),
равносильного искомому условие (3)
теоремы оказалось выполненным.
