Определенный интеграл

И зучение определенного интеграла начинаем со следующей задачи. Пусть функция

определена на 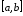, . Попробуем отыскать метод вычисления площади фигуры (криволинейной трапеции), ограниченной осью , прямыми , и графиком функции , рис. 1.

Рассмотрим частные случаи

1. Функция постоянна на . В таком случае рассматриваемая фигура является прямоугольником, а его площадь равна длине основания , умноженной на высоту

.

2. Пусть непрерывна на . Разделим отрезок на произвольных частей точками . Выберем на каждом элементарном отрезке произвольную точку и вычислим значение функции в ней, т.е. величину .

Умножим найденные значения на длину , т.е. .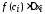

Составим сумму всех таких произведений

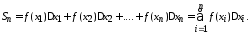(6)

Сумма вида (6) называется интегральной суммой функции на отрезке .

Обозначим .

Найдем предел интегральной суммы (6), когда так, что .

Если при этом интегральная сумма имеет предел, который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число называется определенным интегралом от функции на отрезке и обозначается

Числа a и b называются, соответственно, нижним и верхним пределами интегрирования, - подынтегральной функцией, - подынтегральным выражением, - переменной интегрирования, - областью интегрирования.

Теорема существования определенного интеграла

Если функция 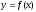непрерывна на , то определенный интеграл существует.

Укажем на некоторые свойства определенного интеграла:

1. Определенный интеграл не зависит от обозначения переменной интегрирования .

2. 

3. Для любого с, .

Теорема. Если функция непрерывна на , то определенный интеграл с переменным верхним пределом является первообразной для функции , то есть

Формула Ньютона - Лейбница

Если _- первообразная для непрерывной на функции , то имеет место равенство:

(7)

Формула Ньютона - Лейбница дает удобный способ вычисления определенного интеграла.

Примеры 26.

Формула Ньютона - Лейбница лежит в основе следующих методов, полезных при вычислении определенных интегралов.

Замена переменных в определенном интеграле

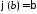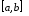Пусть - непрерывна на . Введем новую переменную по формуле . Пусть , , функции , и непрерывны на . Тогда

Пример 27.

Положим

Интегрирование по частям

Для любых непрерывно дифференцируемых на функций и имеет место равенство:

Или в обозначениях

Примеры 28. Вычислить:

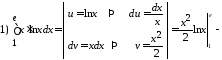
Несобственные интегралы

Пусть теперь функция определена и непрерывна на бесконечном интервале . Тогда для любого значение интеграла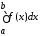 определено и зависит от . Если существует конечный предел , то этот предел называется несобственным интегралом

от на и обозначается через .

В этом случае говорят, что сходится.

В противном случае, т.е. когда конечного предела для интеграла при не существует, говорят о расходимости несобственного интеграла .

Аналогично, определяются следующие несобственные интегралы для других бесконечных пределов

где с - произвольное число.

Примеры 29.

1. Вычислить:

2) Установить, при каких интеграл сходится?

Пусть . Тогда

Таким образом,

Значит, если , то , т. е. интеграл сходится.

Если , то , т. е. интеграл расходится.

При a=1, , т. е. интеграл расходится.

3. 

Интеграл расходится, т. к. предел не существует.

Пусть теперь функция непрерывна на интервале и . Если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают

Таким образом, по определению

Если предел в правой части существует, то несобственный интеграл сходится.

Если же указанный предел не существует или бесконечен, то говорят, что несобственный интеграл расходится.

Аналогично, если функция терпит разрыв в точке , то полагают

Если же функция терпит разрыв во внутренней точке отрезка , то несобственный интеграл определяется формулой

В этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

Пример 30. Вычислить, если он сходится, несобственный интеграл