
- •111Equation Chapter 1 Section 1министерство образования и науки российской федерации
- •«Национальный исследовательский
- •Матанализ 3
- •Аннотация
- •Матанализ 3
- •130102 «Технология геологической разведки»,022000 «Экология и природопользование»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
- •I. Интегральное исчисление функции одной переменной Неопределенный интеграл
- •Определенный интеграл
- •II. Дифференциальные уравнения
- •Основные свойства неопределенного интеграла
- •Полезно помнить таблицу дифференциалов:
- •Непосредственное интегрирование
- •Метод подстановки
- •Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •Примеры интегрирования рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Рассмотрим частные случаи
- •Теорема существования определенного интеграла
- •Интеграл расходится, т. К. Предел не существует. Пусть теперь функция непрерывна на интервалеи. Если существует конечный предел, то его называют несобственным интегралом второго рода и обозначают
- •Функция определена на , и то есть мы имеем дело с несобственным интегралом от функции с бесконечным разрывом. Таким образом,
- •Некоторые приложения определенного интеграла
- •1. Вычисление площади плоской фигуры
- •2. Длина дуги кривой
- •3. Объем тела
- •II. Дифференциальные уравнения Дифференциальные уравнения первого порядка
- •1. Уравнения с разделяющимися переменными
- •Умножим обе части уравнения на 2
- •2. Уравнения, приводящиеся к уравнениям с разделяющимися переменными Уравнения вида
- •3. Однородные уравнения
- •Разделим переменные
- •4. Линейные дифференциальные уравнения первого порядка
- •Решение линейного уравнения методом подстановки
- •5. Уравнение Бернулли
- •Преобразованное уравнение (26) является линейным относительно и. Решив его, найдем общий интеграл уравнения (26). Далее, подставив , получим общее решение уравнения Бернулли (24).
- •6. Уравнение в полных дифференциалах
- •Нахождение общего решения уравнения
- •III. Числовые ряды Если каждому натуральному числу поставлено в соответствие некоторое вполне определенное число, то говорят, что задана числовая последовательность.
- •1. Интегральный признак Коши
- •Следовательно, обобщенный гармонический ряд сходится прии расходится при.
- •Решение. Составим ряд из модулей Получим гармонический ряд, который расходится. Проверим условия признака Лейбница:
- •IV. Функциональные ряды
- •V. Степенные ряды
- •1. Теорема Абеля
- •Решение.
- •3. Методы разложения функций в ряд Тейлора
- •Решение. Воспользуемся формулой суммы бесконечно убывающей геометрической прогрессии
- •Данное разложение имеет место для всех . Варианты заданий для контрольной работы № 6
- •Учебно-методическое обеспечение дисциплины Литература обязательная
5. Уравнение Бернулли
Определение. Уравнение вида
 (24)
(24)
называется
уравнением Бернулли, где
 и
и непрерывные функции от
непрерывные функции от ,
, ,
,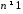 .
.
Замечание.
При
 получается линейное уравнение первого
порядка относительно
получается линейное уравнение первого
порядка относительно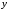 и
и ,
а при
,
а при получается уравнение с разделяющимися
переменными.
получается уравнение с разделяющимися
переменными.
Уравнение Бернулли приводится к линейному следующим образом:
Разделим
все члены уравнения (24) на


 (25)
(25)
Сделаем
замену:

Тогда

Подставим
 в уравнение (25) вместо
в уравнение (25) вместо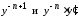

Умножим
полученное уравнение на
 :
:
 (26)
(26)
Преобразованное уравнение (26) является линейным относительно и. Решив его, найдем общий интеграл уравнения (26). Далее, подставив , получим общее решение уравнения Бернулли (24).
Замечание.
При интегрировании уравнений Бернулли
можно сразу применить подстановку
 ,
не преобразовывая их в линейные.
,
не преобразовывая их в линейные.
Пример 14. Решить задачу Коши

Решение.
Разделим уравнение на


Получим
уравнение Бернулли, т. к. в правую часть
входит у
и у',


 .
.
Решение ищем в виде:
 (см.
Замечание),
(см.
Замечание),

Подставим
 и
и в уравнение
в уравнение получим
получим

Вынесем за скобки в первой степени

Полагая,
что
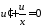 ,
имеем
,
имеем
Запишем систему уравнений

Решая первое уравнение системы, найдем его частное решение.
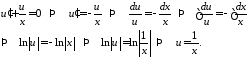
Подставим
 во
второе уравнение системы и найдем её
общее решение.
во
второе уравнение системы и найдем её
общее решение.

Интегрируя левую часть уравнения, получаем

Интеграл,
стоящий в правой части равенства, найдем
с помощью формулы интегрирования по
частям

Вычислим:


Окончательно получим

Умножим
последнее равенство на (1) и выразим из
него функцию
 .
.

Тогда общий интеграл уравнения Бернулли имеет вид:

Воспользуемся
начальными условиями у(1)
= 1 и найдем
 .
.

Подставив с = 0 в общее решение уравнения, найдем его частное решение:

6. Уравнение в полных дифференциалах
Определение. Дифференциальное уравнение первого порядка вида
 (27)
(27)
называется
уравнением в полных дифференциалах,
если его левая часть является полным
дифференциалом некоторой функции
 ,
то есть
,
то есть

 (28)
(28)
Для того чтобы уравнение (27) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие
 (29)
(29)
Нахождение общего решения уравнения
Если выполняется условие (29), то уравнение (27) может быть записано в виде

Тогда общий интеграл этого уравнения имеет вид
 (30)
(30)
где
 произвольная постоянная.
произвольная постоянная.
Функция
 может
быть найдена, используя уравнения (28).
может
быть найдена, используя уравнения (28).
Интегрируя
равенство
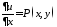 по
по при фиксированном
при фиксированном и учитывая, что произвольная постоянная
в этом случае может зависеть от
и учитывая, что произвольная постоянная
в этом случае может зависеть от ,
получим
,
получим
 (31)
(31)
Затем,
дифференцируя найденную функцию
 по
по и подставляя её в равенство
и подставляя её в равенство ,
найдем
,
найдем .
.
Подставим
функцию
 в уравнение (31), получим
в уравнение (31), получим ,
которая является общим интегралом
уравнения (27) с точностью до произвольной
постоянной.
,
которая является общим интегралом
уравнения (27) с точностью до произвольной
постоянной.
Замечание.
Для нахождения общего решения уравнения
(27) можно было
начать с интегрирования равенства
 при фиксированном
при фиксированном
 .
Тогда постоянная интегрирования может
зависеть от
.
Тогда постоянная интегрирования может
зависеть от
 .
.
Пример
15.
Решить уравнение

Решение.

Проверим
условие (29): 
Следовательно,
левая часть уравнения есть полный
дифференциал некоторой функции
 и решение будет иметь вид:
и решение будет иметь вид:

Воспользуемся условиями (28).
Тогда

Проинтегрируем первое соотношение по х:

Затем
продифференцируем
 по
по :
:

Так
как
 ,
то получим
,
то получим

Отсюда

Пусть

Тогда
 и
общий интеграл уравнения имеет вид
и
общий интеграл уравнения имеет вид

