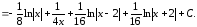- •111Equation Chapter 1 Section 1министерство образования и науки российской федерации
- •«Национальный исследовательский
- •Матанализ 3
- •Аннотация
- •Матанализ 3
- •130102 «Технология геологической разведки»,022000 «Экология и природопользование»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
- •I. Интегральное исчисление функции одной переменной Неопределенный интеграл
- •Определенный интеграл
- •II. Дифференциальные уравнения
- •Основные свойства неопределенного интеграла
- •Полезно помнить таблицу дифференциалов:
- •Непосредственное интегрирование
- •Метод подстановки
- •Метод интегрирования по частям
- •Интегрирование рациональных дробей
- •Алгоритм интегрирования рациональной дроби
- •Примеры интегрирования рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Рассмотрим частные случаи
- •Теорема существования определенного интеграла
- •Интеграл расходится, т. К. Предел не существует. Пусть теперь функция непрерывна на интервалеи. Если существует конечный предел, то его называют несобственным интегралом второго рода и обозначают
- •Функция определена на , и то есть мы имеем дело с несобственным интегралом от функции с бесконечным разрывом. Таким образом,
- •Некоторые приложения определенного интеграла
- •1. Вычисление площади плоской фигуры
- •2. Длина дуги кривой
- •3. Объем тела
- •II. Дифференциальные уравнения Дифференциальные уравнения первого порядка
- •1. Уравнения с разделяющимися переменными
- •Умножим обе части уравнения на 2
- •2. Уравнения, приводящиеся к уравнениям с разделяющимися переменными Уравнения вида
- •3. Однородные уравнения
- •Разделим переменные
- •4. Линейные дифференциальные уравнения первого порядка
- •Решение линейного уравнения методом подстановки
- •5. Уравнение Бернулли
- •Преобразованное уравнение (26) является линейным относительно и. Решив его, найдем общий интеграл уравнения (26). Далее, подставив , получим общее решение уравнения Бернулли (24).
- •6. Уравнение в полных дифференциалах
- •Нахождение общего решения уравнения
- •III. Числовые ряды Если каждому натуральному числу поставлено в соответствие некоторое вполне определенное число, то говорят, что задана числовая последовательность.
- •1. Интегральный признак Коши
- •Следовательно, обобщенный гармонический ряд сходится прии расходится при.
- •Решение. Составим ряд из модулей Получим гармонический ряд, который расходится. Проверим условия признака Лейбница:
- •IV. Функциональные ряды
- •V. Степенные ряды
- •1. Теорема Абеля
- •Решение.
- •3. Методы разложения функций в ряд Тейлора
- •Решение. Воспользуемся формулой суммы бесконечно убывающей геометрической прогрессии
- •Данное разложение имеет место для всех . Варианты заданий для контрольной работы № 6
- •Учебно-методическое обеспечение дисциплины Литература обязательная
Интегрирование рациональных дробей
Рациональной
дробью называется дробь вида
 ,
где
,
где и
и – многочлены степени
– многочлены степени и
и соответственно.
Рациональная дробь называетсяправильной,
если степень числителя меньше степени
знаменателя (
соответственно.
Рациональная дробь называетсяправильной,
если степень числителя меньше степени
знаменателя ( <
< ),
в противном случае дробь называетсянеправильной.
),
в противном случае дробь называетсянеправильной.
Простейшими элементарными дробями называются дроби следующего вида:
 ;
; ,
,
 >1,
целое;
>1,
целое; ,
где
,
где
 <
0, т. е. квадратный трехчлен не имеет
действительных корней;
<
0, т. е. квадратный трехчлен не имеет
действительных корней;
 ,
где
,
где
 <
0, т. е. квадратный трехчлен не имеет
действительных корней.
<
0, т. е. квадратный трехчлен не имеет
действительных корней.
Пример 10.

 ,
здесь
,
здесь
 .
.
Пример 11.

Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Пример 12.
 =
=


 ;
;
Возвращаясь к старой переменной, получим:
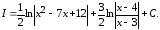
Алгоритм интегрирования рациональной дроби
Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
 ,
где
,
где многочлен,
а
многочлен,
а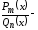 правильная
рациональная дробь.
правильная
рациональная дробь.
Знаменатель
 разложим
на простейшие сомножители:
разложим
на простейшие сомножители:
 ,
где многочлены
,
где многочлены
 не имеют действительных корней.
не имеют действительных корней.
Представим дробь
 в виде суммы простейших дробей с
неопределенными коэффициентами.
в виде суммы простейших дробей с
неопределенными коэффициентами.

 ,
,
где
 - неопределенные коэффициенты, которые
надо найти.
- неопределенные коэффициенты, которые
надо найти.
Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях
 .
.Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая
 равным
действительным корням знаменателя.
равным
действительным корням знаменателя.Подставим найденные коэффициенты
 в разложение дроби.
в разложение дроби.Проинтегрируем простейшие дроби.
Примеры интегрирования рациональных функций
Пример
13.  =
= ;
;
 −это
неправильная рациональная дробь. Сначала
выделим целую часть дроби, разделив
числитель на знаменатель.
−это
неправильная рациональная дробь. Сначала
выделим целую часть дроби, разделив
числитель на знаменатель.
-


-
2
Тогда
 ,
где
,
где – целая часть дроби,
– целая часть дроби, – правильная рациональная дробь,
знаменатель которой разлагается на
множители:
– правильная рациональная дробь,
знаменатель которой разлагается на
множители: .
.
Корни
знаменателя:
 ,
а
,
а не имеют действительных корней.
не имеют действительных корней.
Тогда разложение для данной дроби имеет вид:
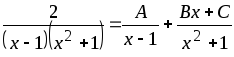 .
.
Приводя полученные дроби к общему знаменателю, получим тождество:
 .
.
Приравнивая числители обеих дробей, получим уравнение:
2=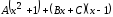 .
.
Пусть
 ,
тогда 2=2
,
тогда 2=2
 .
Коэффициенты
.
Коэффициенты найдем из системы:
найдем из системы:


Откуда
 .
.
Тогда
 =
= =
=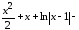
 =
=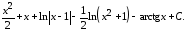
Пример
14.  .
.
 –правильная
дробь. Разложим знаменатель на простейшие
сомножители, получим:
–правильная
дробь. Разложим знаменатель на простейшие
сомножители, получим:
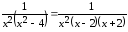 .
.
Корни
знаменателя:
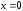 – кратности 2 и
– кратности 2 и
 – простые корни.
– простые корни.
Запишем разложение правильной рациональной дроби на сумму простейших:
 .
.
Приведем дроби к общему знаменателю, затем приравняем числители обеих дробей. Получим тождество:
 .
.
Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.


Откуда
 ,
, ,
, .
.
Чтобы
найти коэффициент
 составим уравнение, приравнивая
коэффициенты при
составим уравнение, приравнивая
коэффициенты при слева и справа в тождестве.
слева и справа в тождестве.
Получим
уравнение:
 Откуда
Откуда .
.
Подставим найденные коэффициенты в разложение и проинтегрируем дроби.