Число ненулевых констант в тензорах II, II и iу ранга

сингония	Число независимых констант у тензоров 2, 3 и 4-го рангов
	2й ранг	3й ранг	4й ранг
Моноклинная ii,yz,xz,xy Триклинная xx,yy,zz,yz Тетрагональная xx=yy,zz Тригональная xx=yy,zz Гексагональная xx=yy,zz Кубическая xx=yy=zz	6 4 2 2 2 1	18,0 10,8,0 1,2,3,4 6,4,2,0 1,2,3,4 0	21 13 7,6 7,6 5 3
Изотропная среда	1	0	2

2.3 Закон Гука. Модули упругости и упругие константы.

Если деформации _ij, возникающие при приложении к твердому телу механического напряжения _kl, малы, то они пропорциональны этим напряжениям (закон Гука):

_xx=s_xxxx_xx+s_xxyy_yy+s_xxzz_zz+s_xxzy_zy+s_xxzx_zx+s_xxxy_xy

_yy=s_yyxx_xx+s_yyyy_yy+s_yyzz_zz+s_yyzy_zy+s_yyzx_zx+s_yyxy_xy

_zz=s_zzxx_xx+s_zzyy_yy+s_zzzz_zz+s_zzzy_zy+s_zzzx_zx+s_zzxy_xy

_zy=s_zyxx_xx+s_zyyy_yy+s_zyzz_zz+s_zyzy_zy+s_zyzx_zx+s_zyxy_xy

_zx=s_zxxx_xx+s_zxyy_yy+s_zxzz_zz+s_zxzy_zy+s_zxzx_zx+s_zxxy_xy

_xy=s_xyxx_xx+s_xyyy_yy+s_xyzz_zz+s_xyzy_zy+s_xyzx_zx+s_xyxy_xy

или в краткой записи с учетом суммирования по повторяющимся индексам

_i = s_ijkl _kl ,

где s_ijkl – модули упругости (постоянные упругости, постоянные упругой податливости), Можно написать и обратное соотношение, связывающее механическое напряжение и механическую деформацию:

_kl = c_klij _ij ,

где c_klij – упругие постоянные (константы жесткости).

Модули упругости s_ijkl и упругие постоянные c_klij являются элементами тензора IY ранга, связывающего два тензора второго ранга. Полное число элементов тензора четвертого ранга равно 3⁴=81. Однако, поскольку тензор механического напряжения и тензор деформации симметричные тензоры (т.е. инвариантны относительно перестановки значков), компоненты тензора упругих постоянных также инвариантны относительно перестановок двух пар индексов ij и kl , так что из 81 компонент независимыми остаются только 36. Физический смысл отдельных компонент можно понять, предполагая, что на кристалл действуют различные простые напряжения. При приложении чистого сдвигового напряжения ₁₂=₂₁ (₁₂ не может быть в отсутствие объемных моментов приложено без ₂₁) элемент ₁₁ тензора деформации был бы равен (здесь использована замена x1, y2, z3):

₁₁=s₁₁₁₂₁₂+s₁₁₂₁₂₁=(s₁₁₁₂+s₁₁₂₁)₁₂.

Все сказанное для тензора модулей упругости s_ijkl справедливо также и для тензора упругих постоянных c_klij.

Благодаря симметричности s_ijkl и c_klij по первым двум и последним двум индексам, можно применить более короткую запись с использованием так называемых матричных обозначений. В этой записи пары первых и последних индексов заменяются одним индексом, пробегающим значения от 1 до 6 по следующим правилам:

Тензорные обозначения 11 22 33 23,32 31,13 12,21

Матричные обозначения 1 2 3 4 5 6.

При этом для тензора упругой податливости s_klij вводятся множители 2 и 4 следующим образом:

s_ijkl = s_mn при m,n=1,2,3

2s_ijkl = s_mn при m,n=4,5,6

4s_ijkl = s_mn при и m и n=4,5,6.

Для тензора упругих постоянных c_ijkl множители 2 и 4 вводить не нужно, т.е. всегда c_ijkl = c_mn.

Тензор механических напряжений и деформаций в матричной записи выглядит так:

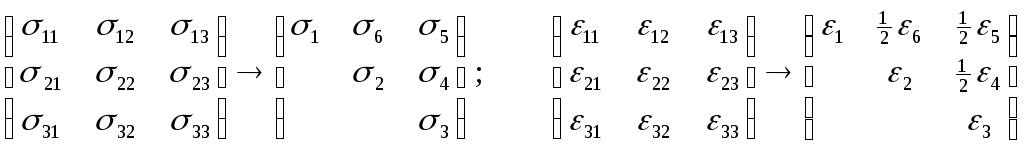
Закон Гука, следовательно, более кратко можно записать следующим образом:

_I = s_ij_j _I = c_ij _j i, j=1,2,3,4,5,6.

Таблицы |s_mn| и |с_mn| представляют собой квадратные матрицы 6х6 и, разумеется, не являются, несмотря на наличие двух индексов, тензорами II ранга. Поскольку матрицы коэффициентов |s_mn| и |с_mn| симметричны, число назависимых упругих констант может быть только 21 (6 диагональных элементов и (36–6)/2=15 недиагональных).Это можно показать, рассматривая энергию деформированного тела. Действительно, при упругой деформации твердого тела, выполненная работа идет на увеличение свободной энергии деформированного кристалла и должна выражаться через величину деформации _ij и упругие постоянные c_ijkl.

Рассмотрим малый куб кристалла с единичным ребром, на который действуют компоненты механического напряжения _ij . Если в рассматриваемом кубе возникает только деформация сжатия., т.е. компоненты деформации _xx, _yy, _zz изменяются соответственно на _xx, _yy, _zz,, то работа производится только нормальными компонентами напряжений и поэтому равна:

W₁=_xx_xx+_yy_yy+_zz_zz

Если же рассматриваемый куб претерпевает и деформацию сдвига, то противоположные грани куба смещаются в противоположных направлениях на величину _xy, _xz и _yz , а компонента силы, действующая на грани равняется _xy, _xz и _yz , так что работа этих сил равна:

W₂=_xy_xy+_xz_xz+_yz_yz .

В итоге полная запасенная энергия деформации (или выполненная работа) на единицу объема в тензорной свернутой записи равна:

W = _ij _ij i, j =1,2,3; W =_k _k k=1,2,3,4,5,6.

Если выполняется закон Гука, это уравнение принимает вид:

W = c_ijkl _ij _kl или W =c_mn _n _m.

Следовательно,

поскольку W есть функция состояния тела, определяемого компонентами деформации, то порядок дифференцирования не имеет значения, так что левая сторона соотношения симметрична по перестановке индексов kl. Поэтому c_kl=c_lk и, разумеется, s_kl=s_lk, и благодаря симметричности матриц число независимых констант жесткости и податливости уменьшается до 21.

4. Упругие волны в кристалле

Случайные флюктуации деформации в кристалле приводят к появлению напряжений, вызывающих распространение деформаций в среде. Если  – плотность кристалла, и на элементарный объем xyz действуют силы, выраженные через напряжения _ij, то можно написать уравнения движения среды вдоль направления x (см. рис.16):

.

Рис.16. Неравновесные напряжения в макроскопическом кубе кристалла, возникающие в результате флюктуаций и вызывающие неравновесную деформацию среды и как следствие механические колебания в кристалле. Показаны механические напряжения, действующие на все грани куба вдоль направления x. Силы, действующие на эти грани, равны произведению величины напряжения на площадь грани, так что легко написать уравнение движения среды вдоль оси x.

Аналогично для направлений y и z:

(d²u/dt²)=(d_xx/dx)+(d_xy/dy)+(d_xz/dz)

(d²v/dt²)=(d_yx/dx)+(d_yy/dy)+(d_yz/dz)

(d²w/dt²)=(d_zx/dx)+(d_zy/dy)+(d_zz/dz)