Основные виды звеньев механизма

№ п/п	Название		Условное изображение на схемах			Движение	Особенности
1	2		3			4	5
1	Стойка					Отсутствует
2	Стойка					Отсутствует
3	Кривошип					Вращательное	Полный оборот
4	Шатун					Сложное	Нет пар, связанных со стойкой
5	Коромысло					Качательное	Неполный оборот, возвратно-вращательное движение
6	Ползун					Возвратно-поступательное	Направляющая неподвижна
7	Кулиса (1) Камень (2)					Вращательное, колебательное	Направляющая подвижна
8		Кулиса (1) Камень (2)			Сложное			Направляющая подвижна
9		Кулиса (1) Камень (2)			Возвратно-поступательное			Направляющая подвижна
10		Кулачок (1) Толкатель (2)			Вращательное, колебательное			Профиль определяет закон движения ведомого звена
11		Кулачок (1) Толкатель (2)			Возвратно поступательное			Профиль определяет закон движения ведомого звена
12		Зубчатое колесо			Вращательное, колебательное			Зубчатый контур
13		Фрикционное колесо			Вращательное, колебательное
14		Рейка			Возвратно-поступательное			Может иметь зубчатый контур

Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой.

Кинематические пары различают по характеру соприкосновения звеньев. Пару называют низшей, если контакт осуществляется по поверхности, и высшей, если контакт происходит по линии или в точке.

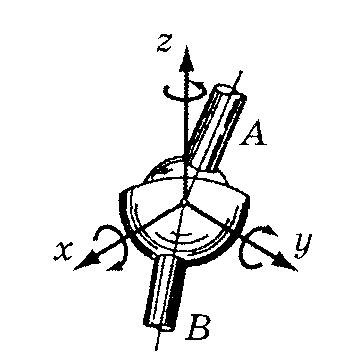
По классификации И. И. Артоболевского класс кинематической пары определяется числом условий связи, наложенных на относительное движение звеньев (табл.1.2)

Таблица 1.2

Классификация кинематических пар

Число условий связи S	Число степеней свободы H	Обозначение кинематической пары	Класс кинематической пары	Название пары	Рисунок	Условное обозначение
1	5		I	Пяти- подвижная шар-плоскость
2	4		II	Четырех-подвижная цилидр-плоскость
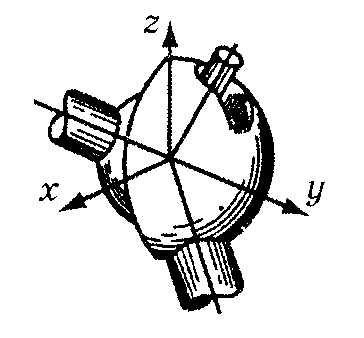
3	3		III	Трех-подвижная плоскостная
3	3		III	Трех-подвижная сферическая
4	2		IV	Двух-подвижная сферическая с пальцем
4	2		IV	Двух-подвижная цилиндрическая
5	1		V	Одно-подвижная винтовая
5	1		V	Одно-подвижная вращательная
5	1		V	Одно-подвижная поступательная

Система звеньев, образующих между собой кинематические пары, называется кинематической цепью.

Механизмом называется такая кинематическая цепь, в которой при заданном движении одного или нескольких звеньев, обычно называемых входными или ведущими, относительно любого из них (например, стойки) все остальные совершают однозначно определяемые движения.

Механизм называется плоским, если все точки звеньев, образующих его, описывают траектории, лежащие в параллельных плоскостях.

Кинематическая схема механизма является графическим изображением механизма, выполненным в масштабе посредством условных обозначений звеньев и кинематических пар. Она дает полное представление о структуре механизма и размерах звеньев, необходимых для кинематического анализа.

Структурная схема механизма в отличие от кинематической схемы может быть выполнена без соблюдений масштаба и дает представление лишь о структуре механизма.

Числом степеней свободы механизма называется число не­зависимых координат, определяющих положение всех звеньев относительно стойки. Каждая из таких координат называется обобщенной. То есть число степеней свободы механизма рав­но числу обобщенных координат.

Для определения числа степеней свободы пространствен­ных механизмов применяется структурная формула Сомова-Малышева:

W = 6n - 5p₁ - 4p₂ - 3p₃ - 2p₄ - 1p₅, (1.1)

где: W - число степеней свободы механизма;

n - число подвижных звеньев;

р₁, р₂, р₃, р₄, р₅ - соответственно число одно-, двух-, трех-, четырех и

пятиподвижных кинематических пар;

6 - число степеней свободы отдельно взятого тела в про­странстве;

5, 4, 3, 2, 1 - число условий связи, накладываемое соот­ветственно

на одно-, двух-, трех-, четырех и пятиподвижные пары.

Для определения числа степеней свободы плоского меха­низма используется структурная формула Чебышева:

W = 3n - 2p₁, - 1p₂, (1.2)

где: W - число степеней свободы плоского механизма;

n - число подвижных звеньев;

р₁ - число одноподвижных кинематических пар, являю­щихся в

плоскости низшими кинематическими парами;

р₂ - число двуподвижных кинематических пар, которые в плоскости

являются высшими;

3 - число степеней свободы тела на плоскости ;

2 - число связей, накладываемое на низшую кинематиче­скую

пару;

1- число связей, накладываемое на высшую кинематиче­скую пару.

По степени подвижности определяют количество входных звеньев механизма. При получении при расчёте степени подвижности, равной 0 или больше 1, необходимо проверить наличие у механизма пассивных связей или лишних степеней свободы.

Формулы Сомова-Малышева и Чебышева называются структурными, так как они связывают число степеней свободы механизма с числом его звеньев и числом и видом кинема­тических пар.

При выводе этих формул предполагалось, что все нало­женные связи независимы, т.е. ни одна из них не может быть получена как следствие других. В некоторых механизмах это условие не выполняется, т.е. в общее число наложенных свя­зей может войти некоторое число q избыточных (повторных, пассивных) связей, которые дублируют другие связи, не изме­няя подвижности механизма, а только обращая его в статиче­ски неопределимую систему. В этом случае при использова­нии формул Сомова-Малышева и Чебышева эти повторные связи надо вычитать из числа наложенных связей:

W = 6n - (5р₁ + 4р₂ + Зр₃ + 2р₄ + р₅ - q),

W = 3n - (2p₁+ p₂ - q),

откуда q = W - 6n + 5p₁ + 4р₂ + Зр₃ + 2р₄ + p₅,

или q = W - 3n +2p₁ + р₂.

В общем случае в последних уравнениях два неизвест­ных (W и q) и их нахождение представляет собой трудную задачу.

Однако в некоторых случаях W может быть найдено из геометрических соображений, что позволяет определить и q, воспользовавшись последними уравнениями.

Наличие избыточных связей требует повышенной точности изготовления элементов кинематических пар во избежание до­полнительных нагрузок на звенья механизма, увеличения сил и моментов трения в кинематических парах. Например, при не­точности изготовления оси шарниров кривошипно-ползунного механизма (рис. 1.1, а) могут оказаться непараллельными,

Рис. 1.1 а) Кривошипно-ползунный механизм с избыточными

связями (когда оси шарниров непараллельны).

б) тот же механизм без избыточных связей (заменены

кинематические пары В и С).

и механизм превращается в пространственный. В этом случае формула Сомова-Малышева дает следующий результат:

W = 6n - 5p₁, = 6·3-5·4=-2,

т.е. получается не механизм, а ферма, статически неопредели­ма. Число избыточных связей составит (т. к. в реальности W=l):q=l-(-2) = 3.

Избыточные связи в большинстве случаев следует устра­нять, изменяя подвижность кинематических пар.

Например, для рассматриваемого механизма (рис. 1.1, б), заменяя шарнир В двуподвижной кинематической парой (р₂ = 1), а шарнир С — трехподвижной (р₃ = 1), получим:

q = 1 - 6 ·3 + 5 ·2 + 4 ·1 + 3 ·1 = 0,

т.е. избыточных связей нет, и механизм статически определим.

Иногда избыточные связи умышленно вводят в состав меха­низма, например, для повышения его жесткости. Работоспособ­ность таких механизмов обеспечивается при выполнении опре­деленных геометрических соотношений. В качестве примера рассмотрим механизм шарнирного параллелограмма (рис. 1.2, а), у которого АВ//CD, ВС//AD; n = 3, p₁ = 4, W = 1 и q = 0.

Рис. 1.2. Шарнирный параллелограмм:

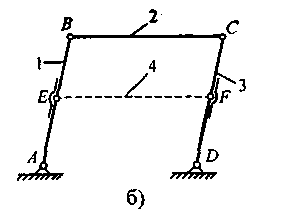
а) без пассивных связей,

б) с пассивными связями

Для повышения жесткости механизма (рис. 1.2, б) вводят дополнительное звено EF, причем при EF//ВС не вносится но­вых геометрических связей, движение механизма не изменяется и в реальности по-прежнему W = 1, хотя по формуле Чебышева имеем: W = 3 · 4 – 2 · 6 = 0, т.е. формально механизм получается статически неопределимым. Однако, если EF не параллельно ВС, движение станет невозможным, т.е. W действительно равно 0.

В соответствии с идеями Л.В. Ассура любой механизм образуется путем последовательного присоединения к механической системе с определенным движением (входным звеньям и стойке) кинематических цепей, удовлетворяющих условию, что степень их подвижности равна 0. Такие цепи, включающие только низшие кинематические пары 5-го класса, называются группами Ассура.

Группа Ассура не может быть разложена на более мелкие группы, обладающие нулевой степенью подвижности.

Группы Ассура подразделяются на классы в зависимости от их строения.

Входное звено, образующее со стойкой низшую кинематическую пару, носит название механизма первого класса (рис 1.3). Степень подвижности этого механизма равна 1.

Рис 1.3. Механизмы первого класса

Степень подвижности группы Ассура равна 0

W=3n-2p₅ = 0.

Из этого условия можно определить соотношение между числом низших кинематических пар пятого класса и числом звеньев, входящих в группу Ассура.

p₅ = 3/2 n.

Отсюда очевидно, что число звеньев в группе должно быть четным, а число пар пятого класса является всегда кратным 3.

Группы Ассура подразделяются на классы и порядки. При сочетании n=2 и p₅=3 образуются группы Ассура второго класса.

Кроме того, группы делятся на порядки. Порядок группы Ассура определяется числом элементов (внешних кинематических пар), которыми группа присоединяется к механизму.

Существуют 5 видов групп Ассура второго класса (табл.1.3).

Класс группы Ассура выше второго определяется числом внутренних кинематических пар, образующих наиболее сложный замкнутый контур.

При сочетании п=4 p₅=6 образуются группы Ассура третьего и четвёртого классов (табл. 1.3). По видам эти группы не различаются.

Общий класс механизма определяется наивысшим классом групп Ассура, входящих в данный механизм.

Формула строения механизма показывает порядок присоединения групп Ассура к механизму первого класса.

Например, если формула строения механизма имеет вид