3.3 Границы страховой надбавки, вычисленные на основе функции полезности страхователя

Пусть 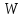– капитал, подверженный риску, а случайные потери этого капитала, т.е.случайная величина с распределением вероятностейна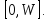Допустим также, что– стоимость (премия) страхования полных потерь, а– стоимость страхования доли, от общей потери, гдеВ случае долевого страхования потерь капиталафинансовое положение страхователя будет представлять собой случайную величину

Найти функцию полезности страхователя и интервал величины страховой премии.

Если отношение страхователя к риску описывается функцией полезности из представления Неймана-Моргенштерна следует, что ожидаемая полезность его финансового состояния будет иметь вид

Конкретизируем теперь функции полезности и распределение вероятностей

Пусть – функция полезности Неймана-Моргенштерна.

Она имеет вид:

Допустим, что распределение потерь описывается плотностью

Графиком этой плотности является:

Таким образом, страхователь претерпевает малые потери гораздо чаще, нежели более крупные.

Нетто-премия Тогда

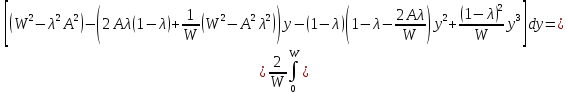
Заметим, что Поэтому функцияпредставляет собой квадратный трехчлен, график которого направлен ветвями вниз. Его вершина соответствует значению

Отсюда видно, что при т.е., максимумдостигается на положительнойи хотя бы частичное страхование является для страхователя приемлемым. Следует отметить также, что в данном случает нетто-премия равна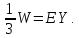Таким образом, возникает промежуток для страховой надбавки:

Выясним условия, при которых . Условиекак уже было показано отвечает неравенствуУсловиеможно записать в виде неравенства

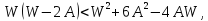
Найденный интервал является величиной, которую согласится платить страхователь за частичное страхование своего капитала

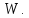
Список использованной литературы:

[1]. Фалин Г. И. Математический анализ рисков в страховании. – М.: Российский юридический издательский дом, 1994.

[2]. Бенинг В. Е., Ротарь В. И. Введение в математическую теорию страхования. – Обозрение прикладной и промышленной математики, 1994, т.29, в.5.

[3]. Бенинг В. Е., Ротарь В. И. Одна модель оптимального поведения страховой компании. – Экономика и математические методы, 1993, т.29, в.4.

[4]. Королёв В. Ю., Бенинг В. Е., Шоргин С. Я. Математические основы теории риска: Учебн. пособ. – М.: ФИЗМАТЛИТ, 2007.

[5]. Arrow K. J. Optimal insurance and generalized deductibles. - Scandinavian Actuar. J., 1974.

[6]. Шахов В. В., Миллерман А. С., Медведев В. Г. Теория и управление рисками в страховании. – М.: Финансы и статистика, 2002.

[7]. Ширяев А. Н. Вероятность: Учебное пособие для вузов. – 2-е издание, преобразованное и дополненное. – М.: Наука. Гл. ред. физ.-мат. лит., 1989.

[8]. Шахов В. В., Миллерман А. С., Медведев В. Г. Теория и управление рисками в страховании. – М.: Финансы и статистика, 2002.

[9]. Вентцель Е. С. Теория вероятностей. – М.: Наука, 1969.

[10]. Eric V. Slud Actuarial Mathematics and Life-Table Statistics. – Mathematics Departament University of Maryland., 2006.

46