2.4 Точный расчет вероятности разорения.

Отправной точкой рассуждений будет уравнение для вероятности разорения которое можно получить переходом к пределу прив уравнении (2.3.5)

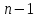Также это уравнение можно получить повторением аргументов, которые привели к уравнению (2.3.5) (нужно заменить ина∞).

Вводя новую переменную интегрирования , мы преобразуем уравнение (2.4.1) к виду:

Дифференцируя по , имеем:

Обращая внимание на наличие свертки, для решения этого уравнения введем преобразования Лапласа

В силу неравенства Лундберга функция определена по меньшей мере для

Поскольку

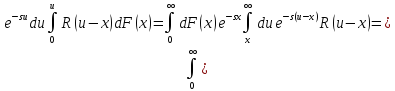
уравнение (2.4.2) для преобразований Лапласа примет вид

Отсюда можно определить преобразование Лапласа вероятности разорения:

При знаменатель дроби в правой части (2.4.3) равен нулю, в то время как. Поэтому числитель этой дроби должен приравняться нулю, что вместе с равенствомдает

И позволяет переписать (2.4.3) в виде

Эта формула дает явное выражение для вероятности разорения в терминах преобразования Лапласа. Для конкретного распределения величины иска можно в явном виде определить и, значит,Полученное явное выражение можно обратить (аналитически или численно) и получить в явном виде зависимостьот величины начальных резервов

Рассмотрим пример.

Предположим, что интенсивность поступления исков 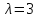, скорость поступления премийа поступающий иск с вероятностьюимеет экспоненциальное распределение со средним, а с вероятностью– экспоненциальное распределение со средним. Определите зависимость вероятности разоренияот величины начальных резервов

Решение. Отметим, что безусловная плотность величины иска является смесью с весамииэкспоненциальных плотностейи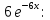

Соответственно преобразование Лапласа величины иска является смесью с весамиипреобразований Лапласа экспоненциальных распределений со среднимии

Аналогичная формула верна и для безусловного среднего значения:

Поэтому относительная защитная надбавка

Подставляя эти явные выражения в общее уравнение (2.4.4) и производя упрощения получим

Для обращения преобразования Лапласа удобно разложить правую часть этого равенства в сумму простейших дробей:

Поскольку дробь вида является преобразованием Лапласа экспоненциальной плотностиотсюда обращением преобразований Лапласа мы получим окончательный результат:

Сопоставим теперь эту точную формулу для вероятности разорения с неравенством Лундберга. Прежде всего подсчитаем характеристический коэффициент.

Преобразование Лапласа величины иска определено дляи дается формулой (2.4.6). Поэтому производящая функция моментовопределена дляи задается формулой

Особо подчеркнем, что хотя правая часть этого равенства определена при всех , она даеттолько для

Поэтому уравнение (2.2.1) для характеристического коэффициента есть:

и после упрощений получим

Это уравнение имеет три корня: Однако поскольку равенство (2.4.8) рассматривается только дляуравнение имеет единственный положительный кореньэто и будет характеристический коэффициент.

Теперь неравенство Лундберга имеет вид:

Поэтому относительная погрешность имеет вид:

Поскольку величина мала, эта погрешность равна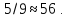

Если использовать эти формулы для вероятности разорения для того, чтобы определить величину резервов , гарантирующую малую вероятность разорения, то погрешность будет меньше.

Например, для точная формула даетв то время как оценка Лундберга даеттак что относительная погрешность равна примерно.